分门别类刷leetcode——二分查找与分治算法(C++实现)
基础复习——二分查找
递归实现二分查找(递归和时间复杂度没有关系)
bool binary_search(vector&sort_array, int begin, int end, int target) {
if (begin > end) return false;
int mid = (begin + end) / 2;
if (target == sort_array[mid]) return true;
else if (target < sort_array[mid])
return binary_search(sort_array, begin, mid - 1, target);
else if(target>sort_array[mid])
return binary_search(sort_array, mid + 1, end, target);
} 循环实现二分查找
bool binary_search(vector&sort_array, int target) {
int begin = 0;
int end = sort_array.size() - 1;
while (begin <= end) {
int mid = (begin + end) / 2;
if (target == sort_array[mid]) return true;
else if (target < sort_array[mid])
end = mid - 1;
else if (target > sort_array[mid])
begin = mid + 1;
}
return false;
}
leetcode 35 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
示例 1:
输入: [1,3,5,6], 5
输出: 2
示例 2:
输入: [1,3,5,6], 2
输出: 1
示例 3:
输入: [1,3,5,6], 7
输出: 4
示例 4:
输入: [1,3,5,6], 0
输出: 0思路:
顺序查找,过了,时间复杂度是O(n),目测面试官不会满意。
class Solution {
public:
int searchInsert(vector& nums, int target) {
if(nums.size()<1) return 0;
for(int i=0; i=target)
return i;
}
return nums.size();
}
};
用二分查找吧。
class Solution {
public:
int searchInsert(vector& nums, int target) {
int index=-1;
int begin=0;
int end=nums.size()-1;
while(index==-1){
int mid=(begin+end)/2;
if(target==nums[mid])
index=mid;
else if(targetnums[mid-1]){
index=mid;
}
end=mid-1;
}else if(target>nums[mid]){
if(mid==nums.size()-1 || target
leetcode 34 在排序数组中查找元素的第一个和最后一个位置
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
你的算法时间复杂度必须是 O(log n) 级别。如果数组中不存在目标值,返回 [-1, -1]。
示例 1:
输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]示例 2:
输入: nums = [5,7,7,8,8,10], target = 6
输出: [-1,-1]思路:
用顺序查找的话,这题不难,二分查找的话,分别找左端点和右端点。写一下二分查找吧。
class Solution {
public:
int left_bound(std::vector& nums, int target){
int begin = 0;
int end = nums.size() - 1;
while(begin <= end){
int mid = (begin + end) / 2;
if (target == nums[mid]){
if (mid == 0 || nums[mid -1] < target){
return mid;
}
end = mid - 1;
}
else if (target < nums[mid]){
end = mid - 1;
}
else if (target > nums[mid]){
begin = mid + 1;
}
}
return -1;
}
int right_bound(vector&nums, int target){
int begin=0;
int end=nums.size()-1;
while(begin<=end){
int mid=(begin+end)/2;
if(target==nums[mid]){
if(mid==nums.size()-1 || nums[mid+1]>target){
return mid;
}
begin=mid+1;
}else if(targetnums[mid]){
begin=mid+1;
}
}
return -1;
}
vector searchRange(vector& nums, int target) {
vectorresult;
result.push_back(left_bound(nums, target));
result.push_back(right_bound(nums, target));
return result;
}
};
leetcode 33 搜索旋转排序数组
假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。
你可以假设数组中不存在重复的元素。你的算法时间复杂度必须是 O(log n) 级别。
示例 1:
输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4
示例 2:
输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1思路:
使用二分查找。将数组一分为二,其中一定有一个是有序的,另一个可能是有序,也能是部分有序。此时有序部分用二分法查找。无序部分再一分为二,其中一个一定有序,另一个可能有序,可能无序。
因此查找过程分为两种情况
- target
- target>nums[mid]
class Solution {
public:
int search(vector& nums, int target) {
int begin=0;
int end=nums.size()-1;
while(begin<=end){
int mid=(begin+end)/2;
if(target==nums[mid])
return mid;
//情况一:target=nums[begin]){
end=mid-1;
}else{
begin=mid+1;
}
//说明nums[mid+1]都numerical[nums.size()-1]为有序区间
}else if(nums[begin]>nums[mid]){
end=mid-1;
//说明此时数组中只有两个元素[6,1],target的值为1
}else if(nums[begin]==nums[mid]){
begin=mid+1;
}
//情况二:target>nums[mid]
}else if(target>nums[mid]){
//mid左侧有序
if(nums[begin]nums[mid]){
//说明mid到数组末尾为有序递增
if(target>=nums[begin]){
//说明目标区间在mid左侧,那段无序区间中
end=mid-1;
}else{
begin=mid+1;
}
}else if(nums[begin]==nums[mid]){
begin=mid+1;
}
}
}
return -1;
}
};
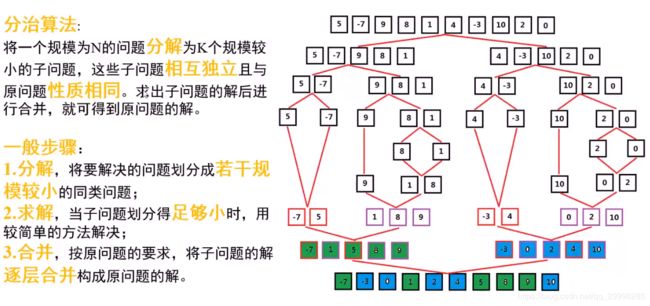
基础复习——分治法
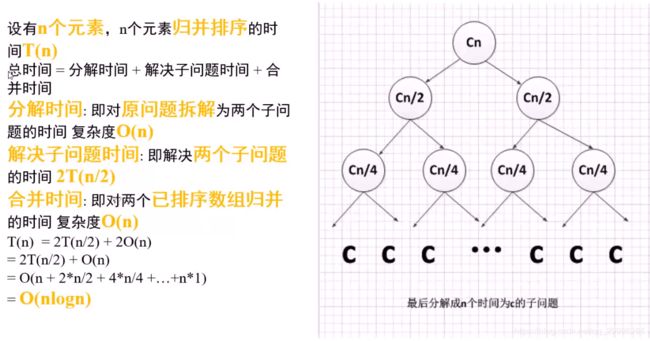
归并排序
递归写法
class Solution {
public:
//归并两个已排序数组
void merge_sort_two_vec(vector&sub_vec1, vector&sun_vec2,
vector&vec){
int i=0, j=0;
while(i&vec){
if(vec.size()<2) return;
int mid=vec.size()/2;
vectorsub_vec1;
vectorsub_vec2;
for(int i=0; i
leetcode 315 计算右侧小于当前元素的个数
给定一个整数数组 nums,按要求返回一个新数组 counts。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例:
输入: [5,2,6,1]
输出: [2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1).
2 的右侧仅有 1 个更小的元素 (1).
6 的右侧有 1 个更小的元素 (1).
1 的右侧有 0 个更小的元素.思路:
class Solution {
public:
vector countSmaller(vector& nums) {
vectorcount;
if(nums.empty()) return count;
vector>vec;
//把每个值以及他在数组中的位置作为pair
for(int i=0; i>&sub_vec1,
vector>&sub_vec2,
vector>&vec,
vector&count){
int i=0, j=0;
while(i>&vec, vector&count){
if(vec.size()<2)
return;
int mid=vec.size()/2;
vector>sub_vec1;
vector>sub_vec2;
for(int i=0; i
leetcode 23 合并K个排序链表
合并 k 个排序链表,返回合并后的排序链表。请分析和描述算法的复杂度。
示例:
输入:
[
1->4->5,
1->3->4,
2->6
]
输出: 1->1->2->3->4->4->5->6方法一:把所有节点都存入数组中,然后对数组进行排序。再将排序好的各个值存入一个新链表中——目测这种方法面试官不喜欢
bool cmp(const ListNode *a, const ListNode *b){
return a->valval;
}
class Solution {
public:
ListNode* mergeKLists(vector& lists) {
vectornode_vec;
for(int i=0; inext;
}
}
if(node_vec.size()==0){
return NULL;
}
sort(node_vec.begin(),node_vec.end(), cmp);
for(int i=1; inext=node_vec[i];
}
node_vec[node_vec.size()-1]->next=NULL;
return node_vec[0];
}
};
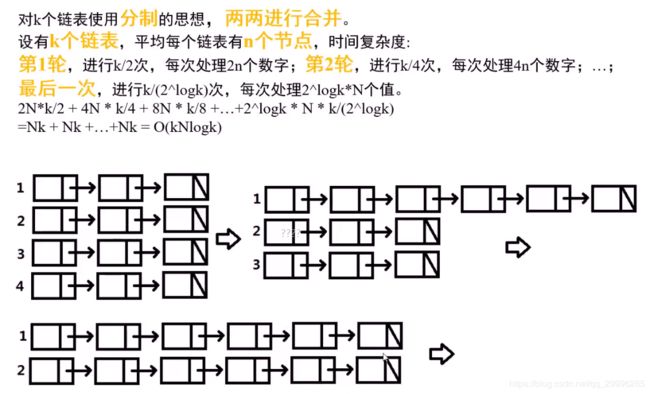
方法二:分治归并
合并两个单链表的步骤:
- 先检查两个链表是否都非空,如果存在空链接,则返回另一个链表的头结点
- 然后设置一个空指针,使其指向两个链表中头结点值较小的节点,将该指针作为结果链表的头结点
- 之后进入循环体,不断比较,直到有一方的链表到达了尾节点为止
- 最后连接剩余的未参与比较的链表段
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
//1
if((!l2)||(!l1)){ //如果存在空链表,则返回另一个链表的头结点
if(l1){
return l1;
}else{
return l2;
}
}
//2
ListNode *result=(l1->val>l2->val)?l2:l1;//结果的头结点
if(result==l1){
l1=l1->next;
}else if(result==l2){
l2=l2->next;
}
//3
ListNode *helper=result;
while(l1&&l2){
if(l1->val>l2->val){
helper->next=l2;
l2=l2->next;
}else{
helper->next=l1;
l1=l1->next;
}
helper=helper->next;
}
//4
//连接l1或l2的剩余节点
if(l1){
helper->next=l1;
}else if(l2){
helper->next=l2;
}
return result;
}
ListNode* mergeKLists(vector& lists) {
if(lists.size()==0) return NULL;
if(lists.size()==1) return lists[0];
if(lists.size()==2) return mergeTwoLists(lists[0], lists[1]);
int mid=lists.size()/2;
vectorsub1_lists;
vectorsub2_lists;
for(int i=0; i