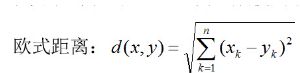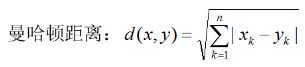机器学习(李航统计学方法)之KNN

说明：代码参考的博客链接为(http://www.pkudodo.com)，隆重推荐! 同时也参考了这位大牛的博客(https://blog.csdn.net/eeeee123456/article/details/79927128)；在Markdown中输入数学公式(MathJax)，参考的博客是(https://www.jianshu.com/p/a0aa94ef8ab2)。若文章有错误，希望各位不吝赐教！我会及时修正！

---

目录

---

1、KNN介绍

KNN,也称K近邻法(k-nearest neighbor)。是一种基本的分类和回归方法，与感知机不一样，感知机是二分类，KNN可以多分类吼！这个算法的做法：给定样本点，基于某种距离度量公式找出训练集中与其最靠近的K个点，然后对这最近的K个最邻近点进行预测。
那么分类和回归有什么不同呢？一般，在分类任务中可使用“投票法”，即选择这k个实例中出现最多的标记类别作为预测结果；在回归任务中可使用“平均法”，即将这k个实例的实值输出标记的平均值作为预测结果；还可基于距离远近进行加权平均或加权投票，距离越近的实例权重越大。此类学习只是把样本全部保存起来，给一个测试样本，然后进行测试。

下面直观了解一下：

感知机，是使用一条直线，即划分超平面的方式来划分数据。而KNN是另一种方式来划分数据。
假设黄点和蓝点表示两种不同的数据。一批零件，黄色表示合格的零件，蓝色表示不合格的零件。那么合格与合格的零件在很多属性上都类似，所以它们会在超平面上“抱团取暖”。那么我们可以看看提供的样本测试点属于哪一堆来判断合格还是不合格。

由上图，我们可以确信前面所写的一句话，KNN可以做多分类，但个人认为这个多分类的方法可以说是“穷举”。因为最简单最初级的分类器是将全部的训练数据所对应的类别都记录下来，当测试对象的属性和某个训练对象的属性完全匹配时，便可以对其进行分类。但怎么可能所有测试对象都会找到与之完全匹配的训练对象呢，其次就是存在一个测试对象同时与多个训练对象匹配，导致一个训练对象被分到了多个类的问题，基于这些问题呢，就产生了KNN。那如何判断出一个特征点与训练集里面“抱团取暖”的点团的距离大小来进行分类？

①找到离这个特征点最近的点就为其所属类。稍微一想，这个方法肯定有问题噻，来个噪声就GG了。随机性太大，你敢保证正确吗？我可不敢保证。。。。。！
②也是看到网友的博客上，计算这个测试点与点团中心的距离。距离最小的类就是所属类。和①一样，不太好，随机性太大。
③找到离这个特征点最近的K个点，选择这k个实例中出现最多的标记类别作为预测结果。怎么说呢，比上面两种好多了，也是K近邻使用的方法。

---

2、KNN算法三要素

KNN算法的三要素是：分类决策规则，K值的选取和距离的度量方式。
分类决策规则：就是上诉所示：③种方法，OK，解决~
K值的选取：额----EMMMMM , 对于k值的选择，没有一个固定的经验，一般根据样本的分布，选择一个较小的值，或者交叉验证选择一个合适的k值，以后接触到的卷积神经网络都不咋用交叉验证，训练时间太慢了。
那么最重要的的就是距离的度量方式。

距离的度量方式

距离度量方式一般分为：欧式距离(Euclidean distance)和曼哈顿距离(Manhattan distance)

2.1 欧式距离(Euclidean distance)

2.2 曼哈顿距离(Manhattan distance)

---

3、KNN算法剖析

在训练集中数据和标签已知的情况下，输入测试数据，将测试数据的特征与训练集中对应的特征进行相互比较，找到训练集中与之最为相似的前K个数据，则该测试数据对应的类别就是K个数据中出现次数最多的那个分类，其算法的描述为：
1）计算测试数据与各个训练数据之间的距离；
2）按照距离的递增关系进行排序；
3）选取距离最小的K个点；
4）确定前K个点所在类别的出现频率；
5）返回前K个点中出现频率最高的类别作为测试数据的预测分类。

4、代码块

代码参考链接：(http://www.pkudodo.com/2018/11/19/1-2/)

# coding=utf-8
# Author:Dodo
# Date:2018-11-16
# Email:[email protected]

'''
数据集：Mnist
训练集数量：60000
测试集数量：10000（实际使用：200）
------------------------------
运行结果：（邻近k数量：25）
向量距离使用算法——欧式距离
    正确率：97%
    运行时长：308s
向量距离使用算法——曼哈顿距离
    正确率：14%
    运行时长：246s
'''

import numpy as np
import time


def loadData(fileName):
    '''
    加载文件
    :param fileName:要加载的文件路径
    :return: 数据集和标签集
    '''
    print('start read file')
    # 存放数据及标记
    dataArr = []
    labelArr = []
    # 读取文件
    fr = open(fileName)
    # 遍历文件中的每一行
    for line in fr.readlines():
        # 获取当前行，并按“，”切割成字段放入列表中
        # strip：去掉每行字符串首尾指定的字符（默认空格或换行符）
        # split：按照指定的字符将字符串切割成每个字段，返回列表形式
        curLine = line.strip().split(',')
        # 将每行中除标记外的数据放入数据集中（curLine[0]为标记信息）
        # 在放入的同时将原先字符串形式的数据转换为整型
        dataArr.append([int(num) for num in curLine[1:]])
        # 将标记信息放入标记集中
        # 放入的同时将标记转换为整型
        labelArr.append(int(curLine[0]))
    # 返回数据集和标记
    return dataArr, labelArr


def calcDist(x1, x2):
    '''
    计算两个样本点向量之间的距离
    使用的是欧氏距离，即 样本点每个元素相减的平方  再求和  再开方
    欧式举例公式这里不方便写，可以百度或谷歌欧式距离（也称欧几里得距离）
    :param x1:向量1
    :param x2:向量2
    :return:向量之间的欧式距离
    '''
    return np.sqrt(np.sum(np.square(x1 - x2)))

    # 曼哈顿距离计算公式
    # return np.sum(x1 - x2)


def getClosest(trainDataMat, trainLabelMat, x, topK):
    '''
    预测样本x的标记。
    获取方式通过找到与样本x最近的topK个点，并查看它们的标签。
    查找里面占某类标签最多的那类标签
    （书中3.1 3.2节）
    :param trainDataMat:训练集数据集
    :param trainLabelMat:训练集标签集
    :param x:要预测的样本x
    :param topK:选择参考最邻近样本的数目（样本数目的选择关系到正确率，详看3.2.3 K值的选择）
    :return:预测的标记
    '''
    # 建立一个存放向量x与每个训练集中样本距离的列表
    # 列表的长度为训练集的长度，distList[i]表示x与训练集中第i个样本的距离
    distList = [0] * len(trainLabelMat)
    # 遍历训练集中所有的样本点，计算与x的距离
    for i in range(len(trainDataMat)):
        # 获取训练集中当前样本的向量
        x1 = trainDataMat[i]
        # 计算向量x与训练集样本x的距离
        curDist = calcDist(x1, x)
        # 将距离放入对应的列表位置中
        distList[i] = curDist

    # 对距离列表进行排序
    # argsort：函数将数组的值从小到大排序后，并按照其相对应的索引值输出
    # 例如：
    #   >>> x = np.array([3, 1, 2])
    #   >>> np.argsort(x)
    #   array([1, 2, 0])
    # 返回的是列表中从小到大的元素索引值，对于我们这种需要查找最小距离的情况来说很合适
    # array返回的是整个索引值列表，我们通过[:topK]取列表中前topL个放入list中。
    # ----------------优化点-------------------
    # 由于我们只取topK小的元素索引值，所以其实不需要对整个列表进行排序，而argsort是对整个
    # 列表进行排序的，存在时间上的浪费。字典有现成的方法可以只排序top大或top小，可以自行查阅
    # 对代码进行稍稍修改即可
    # 这里没有对其进行优化主要原因是KNN的时间耗费大头在计算向量与向量之间的距离上，由于向量高维
    # 所以计算时间需要很长，所以如果要提升时间，在这里优化的意义不大。（当然不是说就可以不优化了，
    # 主要是我太懒了）
    topKList = np.argsort(np.array(distList))[:topK]   # 升序排序
    # 建立一个长度时的列表，用于选择数量最多的标记
    # 3.2.4提到了分类决策使用的是投票表决，topK个标记每人有一票，在数组中每个标记代表的位置中投入
    # 自己对应的地方，随后进行唱票选择最高票的标记
    labelList = [0] * 10
    # 对topK个索引进行遍历
    for index in topKList:
        # trainLabelMat[index]：在训练集标签中寻找topK元素索引对应的标记
        # int(trainLabelMat[index])：将标记转换为int（实际上已经是int了，但是不int的话，报错）
        # labelList[int(trainLabelMat[index])]：找到标记在labelList中对应的位置
        # 最后加1，表示投了一票
        labelList[int(trainLabelMat[index])] += 1
    # max(labelList)：找到选票箱中票数最多的票数值
    # labelList.index(max(labelList))：再根据最大值在列表中找到该值对应的索引，等同于预测的标记
    return labelList.index(max(labelList))


def test(trainDataArr, trainLabelArr, testDataArr, testLabelArr, topK):
    '''
    测试正确率
    :param trainDataArr:训练集数据集
    :param trainLabelArr: 训练集标记
    :param testDataArr: 测试集数据集
    :param testLabelArr: 测试集标记
    :param topK: 选择多少个邻近点参考
    :return: 正确率
    '''
    print('start test')
    # 将所有列表转换为矩阵形式，方便运算
    trainDataMat = np.mat(trainDataArr)
    trainLabelMat = np.mat(trainLabelArr).T
    testDataMat = np.mat(testDataArr)
    testLabelMat = np.mat(testLabelArr).T

    # 错误值技术
    errorCnt = 0
    # 遍历测试集，对每个测试集样本进行测试
    # 由于计算向量与向量之间的时间耗费太大，测试集有6000个样本，所以这里人为改成了
    # 测试200个样本点，如果要全跑，将行注释取消，再下一行for注释即可，同时下面的print
    # 和return也要相应的更换注释行
    # for i in range(len(testDataMat)):
    for i in range(200):
        # print('test %d:%d'%(i, len(trainDataArr)))
        print('test %d:%d' % (i, 200))
        # 读取测试集当前测试样本的向量
        x = testDataMat[i]
        # 获取预测的标记
        y = getClosest(trainDataMat, trainLabelMat, x, topK)
        # 如果预测标记与实际标记不符，错误值计数加1
        if y != testLabelMat[i]:
            errorCnt += 1

    # 返回正确率
    # return 1 - (errorCnt / len(testDataMat))
    return 1 - (errorCnt / 200)


if __name__ == "__main__":
    start = time.time()

    # 获取训练集
    trainDataArr, trainLabelArr = loadData('../Mnist/mnist_train.csv')
    # 获取测试集
    testDataArr, testLabelArr = loadData('../Mnist/mnist_test.csv')
    # 计算测试集正确率
    accur = test(trainDataArr, trainLabelArr, testDataArr, testLabelArr, 25)
    # 打印正确率
    print('accur is:%d'%(accur * 100), '%')

    end = time.time()
    # 显示花费时间
    print('time span:', end - start)