AE(Auto Encoder)、VAE(Variational AutoEncoder)、CVAE(Conditional AutoEncoder)解读
最近在研究编码器,阅读大量论文,历程艰辛,特此记录。如果博文有不妥之处,请告知,我一定及时修正!AE(Auto Encoder)、VAE(Variational AutoEncoder)、CVAE(Conditional AutoEncoder)解读
文章目录
- 1、AE(Auto Encoder) 自动编码器
- 2、VAE(Variational AutoEncoder)
- 3、CVAE(Conditional AutoEncoder)
- 4、参考链接
1、AE(Auto Encoder) 自动编码器
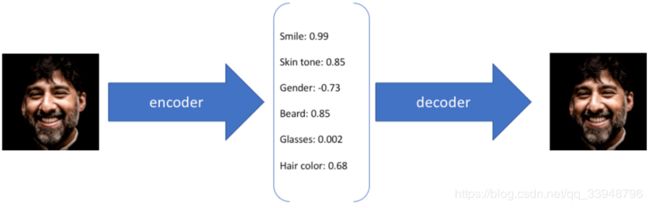 AE分为两个部分:编码器和解码器。编码器可以是任意模型,现在一般都使用卷积神经网络。输入一张图片经过编码器得到潜变量 ( L a t e n t V a r i a b l e ) (Latent \ Variable) (Latent Variable),类似于降维,得到这张图片的主要成分,然后再通过解码网络进行恢复出原图,所以判断编码和解码网络好坏的 L o s s 1 = M S E ( i n p u t , o u t p u t ) Loss1=MSE(input,output) Loss1=MSE(input,output)。
AE分为两个部分:编码器和解码器。编码器可以是任意模型,现在一般都使用卷积神经网络。输入一张图片经过编码器得到潜变量 ( L a t e n t V a r i a b l e ) (Latent \ Variable) (Latent Variable),类似于降维,得到这张图片的主要成分,然后再通过解码网络进行恢复出原图,所以判断编码和解码网络好坏的 L o s s 1 = M S E ( i n p u t , o u t p u t ) Loss1=MSE(input,output) Loss1=MSE(input,output)。
那这个降维得到的潜变量代表什么意思呢?以MNIST为例, 潜变量 Z Z Z就是一个内在的变量, 它在这张图片生成之前先决定了要生成哪一张,这就是 P ( X ∣ Z ) P(X|Z) P(X∣Z)。比如输入一张数字 “7”图片,写这个数字需要什么元素呢?需要一横一竖,横竖之间需要一定的角度。这些元素就是该数字的潜变量。单个潜变量元素分析是没有意义的,也是未知的,稍微改变这个潜变量或者不改变,都能得到数字 “7”,只不过会有偏移,比如粗细,胖瘦,倾斜角度。
对于AE,AE中学习的是 e n c o d e r encoder encoder和 d e c o d e r decoder decoder,只能从一个 X X X,得到对应的重构 X X X。但是无法生成新的样本。重建一张图片是没有什么问题的,但是生成呢?AE无法无输入有效生成,我们无法去构造隐藏向量,因为我们是通过一张图片输入编码得到隐向量的。
那生成如何解决呢?这时候就出现了VAE,简单的说就在编码过程给它增加一些限制,迫使其生成的隐含向量能够粗略的遵循一个标准正态分布。
2、VAE(Variational AutoEncoder)
VAE结构图:
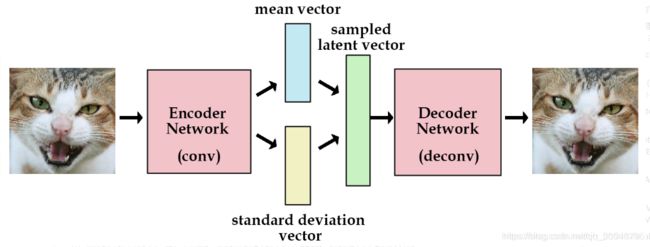
设输入的数据为 X X X,其分布为 P ( X ) P(X) P(X),这个分布是未知的,难采样,所以把 P ( X ) P(X) P(X)改下:
P ( X ) = ∑ z P ( X / Z ) ∗ P ( Z ) P(X)=\sum_{z}P(X/Z)*P(Z) P(X)=z∑P(X/Z)∗P(Z)其中 P ( X / Z ) P(X/Z) P(X/Z)表示用 Z Z Z来表示 X X X的模型。假设最后得到的这个潜变量 Z Z Z服从正态分布,也就是 P ( Z ) = N ( μ , σ 2 ) P(Z)=N(\mu,\sigma^2) P(Z)=N(μ,σ2)。如果满足这个条件,我们就可以从满足正态分布的噪声里采样,得到新的样本。(上述公式可以看成生成便于我们理解)
那么上面的公式目的就修改成为:(下面可以看成编码来看)
P ( Z ) = ∑ x P ( Z / X ) ∗ P ( X ) P(Z)=\sum_{x}P(Z/X)*P(X) P(Z)=x∑P(Z/X)∗P(X)如果我们继续假设 P ( Z / X ) P(Z/X) P(Z/X)为正态分布 N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2),那么上述公式就变为:
P ( Z ) = ∑ x P ( Z / X ) ∗ P ( X ) = N ( μ , σ ) ∗ ∑ x P ( X ) = N ( μ , σ 2 ) P(Z)=\sum_{x}P(Z/X)*P(X)=N(\mu,\sigma)*\sum_{x}P(X)=N(\mu,\sigma^2) P(Z)=x∑P(Z/X)∗P(X)=N(μ,σ)∗x∑P(X)=N(μ,σ2)这就可以啦!这就是下面这张图的思路:
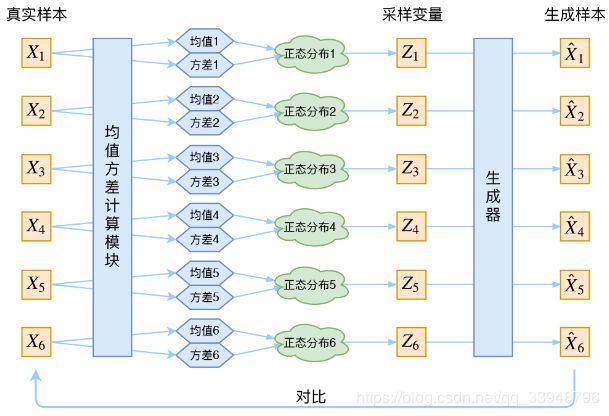
这里我们可以看出每一个样本,都有其专属的正态分布。那么有超多的样本,就有超多的专属分布。正态分布的两组参数(均值 μ \mu μ,方差 σ \sigma σ)(所以这边是个向量)。
V A E VAE VAE里面是使用神经网络来计算均值和方差,详细可以看代码。为什么要使用均值和方差?因为:从 P ( Z ∣ X k ) P(Z∣X_k) P(Z∣Xk)中采样一个 Z k Z_k Zk出来,这个 P ( Z ∣ X k ) P(Z∣X_k) P(Z∣Xk)是正态分布,需要可导便于反向传播。所以利用均值方差,因为均值和方差是靠模型算出来的,这边利用了一个事实:
N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2)采样一个 Z Z Z,相当与从 N ( 0 , 1 ) N(0,1) N(0,1)采样一个 β \beta β,然后让 Z = μ + β ∗ σ Z=\mu+\beta*\sigma Z=μ+β∗σ。
这就是论文中所说的:重参数技巧。
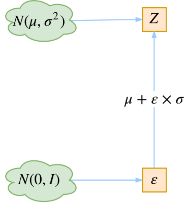
那下面这种图里面为什么要将 P ( Z / X ) P(Z/X) P(Z/X)像标准正态看齐呢?
我个人的理解是: ( μ , σ 2 ) (\mu,\sigma^2) (μ,σ2)中, μ \mu μ为圆点, σ \sigma σ为半径画空间。这里为啥要 σ \sigma σ不为0,目的是防止了噪声为零,同时保证了模型具有生成能力。拿大牛的解释是:VAE本质上就是在常规的自编码器的基础上,对 E n c o d e r Encoder Encoder的结果(在VAE中对应着计算均值的网络)加上了“高斯噪声”,使得结果 D e c o d e r Decoder Decoder能够对噪声有鲁棒性;那另外一个 E n c o d e r Encoder Encoder(计算方差的网络)的作用呢?用来动态调节噪声的强度。

而怎么将 N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2)逼近 N ( 0 , 1 ) N(0,1) N(0,1),论文中使用的是 K L D KLD KLD散度。
这个我前面的博客介绍了:(https://blog.csdn.net/qq_33948796/article/details/88723125)
总结一下: E n c o d e r Encoder Encoder 从图像中采样,产生 L a t e n t s p a c e Latent \ space Latent space 的概率分布, t h e d e c o d e r the \ decoder the decoder 在 L a t e n t s p a c e Latent \ space Latent space中采样该点,然后返回一个生成的图像。所以对于一张给定的图像来说, E n c o d e r Encoder Encoder 产生一个分布,在 L a t e n t s p a c e Latent \ space Latent space 中该分布中采样出一个点出来,然后将该点输入到 D e c o d e r Decoder Decoder 当中,产生一个图像。
3、CVAE(Conditional AutoEncoder)
上述生成是不能控制的,但是现实中很多情况往往是希望能够实现控制某个变量来实现生成某一类图像。CVAE可以实现这个:
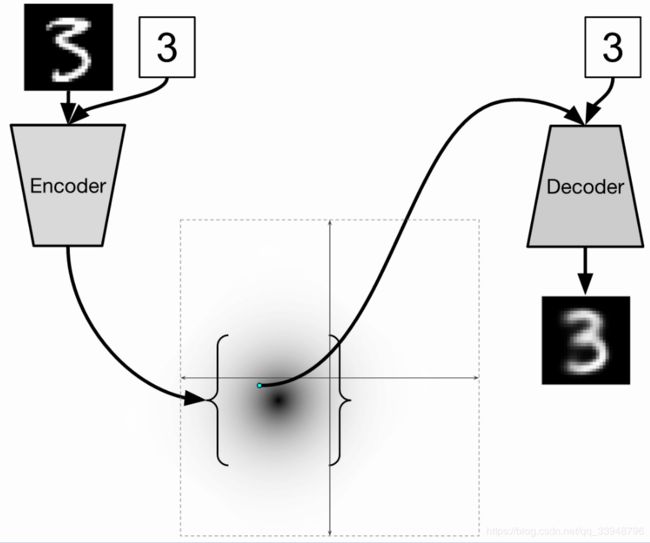
训练的时候,输入给 E n c o d e r Encoder Encoder和 D e c o d e r Decoder Decoder 的图像对应的数字是给定的。在这种情况下,这个标签被表示成 o n e − h o t v e c t o r one-hot \ vector one−hot vector 。
4、参考链接
- https://blog.csdn.net/antkillerfarm/article/details/80648805
- https://www.cnblogs.com/wangxiaocvpr/p/6231019.html