一图读懂“心脑相连”最新成果：艾伦研究所发现心跳时，大脑会抖动

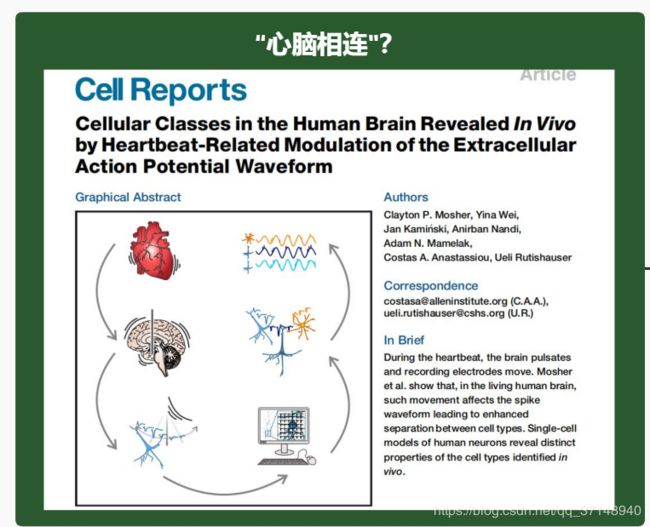
Cell Reports, 作者为Mosher等人: "Cellular classes in the human brain revealed in vivo by heartbeat-related modulation of the extracellular action potential waveform "

是位置改变还是特殊的与心电相关的神经元放电？

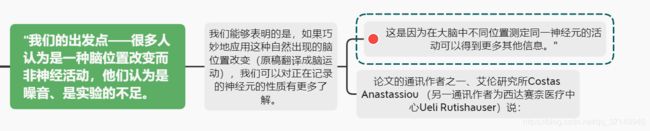
个人觉得“脑运动”这个翻译的不好，根据前文，这里应该是指大脑内神经元的位置改变

这里是对波形的研究
“gamma波及theta波是大脑中与认识高度相关的活动模式。


文章URL（请在上线后访问）：
https://www.cell.com/cell-reports/fulltext/S2211-1247(20)30188-1

Highlights
•
When the heart beats, recording electrodes inside the human brain move
•
Movement elicits features of the action potential that improve cell typing in vivo
•
Human single-cell modeling infers cellular properties of identified cell types
•
Newly detected cell types exhibit differential coupling to local oscillations

当心脏跳动时，记录大脑内部的电极就会移动

在yivo中，运动激发了改善细胞分型的动作电位特征

人类单细胞建模推断已识别的细胞类型的细胞特性

新发现的细胞类型表现出对局部振荡的微分耦合

Summary

Determining cell types is critical for understanding neural circuits but remains elusive in the living human brain. Current approaches discriminate units into putative cell classes using features of the extracellular action potential (EAP); in absence of ground truth data, this remains a problematic procedure. We find that EAPs in deep structures of the brain exhibit robust and systematic variability during the cardiac cycle. These cardiac-related features refine neural classification. We use these features to link bio-realistic models generated from in vitro human whole-cell recordings of morphologically classified neurons to in vivo recordings. We differentiate aspiny inhibitory and spiny excitatory human hippocampal neurons and, in a second stage, demonstrate that cardiac-motion features reveal two types of spiny neurons with distinct intrinsic electrophysiological properties and phase-locking characteristics to endogenous oscillations. This multi-modal approach markedly improves cell classification in humans, offers interpretable cell classes, and is applicable to other brain areas and species.

(翻译）
确定细胞类型对于理解神经回路是至关重要的，但在人类大脑中仍然难以实现。目前的方法利用细胞外动作电位(EAP)的特征将单元划分为假定的细胞类别;在缺乏地面真实数据的情况下，这仍然是一个有问题的过程。我们发现大脑深层结构中的EAPs在心脏周期中表现出强烈的系统变异性。这些与心脏相关的特征完善了神经分类。我们使用这些功能来连接从生物逼真的模型。从形态分类神经元的体外numan全细胞记录到体内记录。我们在第二个staqe中区分了有刺抑制性和有刺兴奋性的人类海马神经元。表明心脏运动特征揭示了两种对内源性振荡具有明显内在电生理特性和锁相特性的多刺神经元。这种多模态方法显著地改进了人类的细胞分类，提供了可解释的细胞类别，并适用于其他大脑区域和物种。

Graphical Abstract
Figure thumbnail fx1
View Large ImageFigure ViewerDownload Hi-res imageDownload (PPT)
Keywords
human recordings
heartbeat
cell types
spike waveform
biophysical modeling
slice physiology
morphology
LFP coupling
hippocampus
cardiovascular
Introduction
Complex behaviors depend on the recruitment and cooperation of many types of excitatory and inhibitory cells within and across brain circuits (Buzsáki, 2006, Klausberger and Somogyi, 2008). Advances in genetic sequencing offer an increasing ability to identify and separate between cell types, giving rise to a more elaborate view of the composition of brain circuits (e.g., Hodge et al., 2018, Soltesz and Losonczy, 2018, Tasic et al., 2018). How these cell types contribute to high-level functions in vivo remains largely unknown. This is particularly true in humans, where little is known about how genetically distinct neural classes differ in their electrophysiological or morphological properties, how they behave in vivo, and how they support cognition (Anastassiou and Shai, 2016, Buzsáki et al., 2012). The primary means of monitoring the activity of brain circuits in vivo are extracellular recordings where putative excitatory and inhibitory cells are identified based on features of the extracellular action potential (EAP) waveform (Buzsáki, 2004, Buzsáki and Draguhn, 2004). More recently, genetic markers and fluorescence imaging have been used to monitor specific types of neurons in rodents (Kohara et al., 2014, Senzai and Buzsáki, 2017) and monkeys (Stauffer et al., 2016). Such cell-type-specific resolution is lacking in humans because genetic manipulation in vivo remains infeasible.
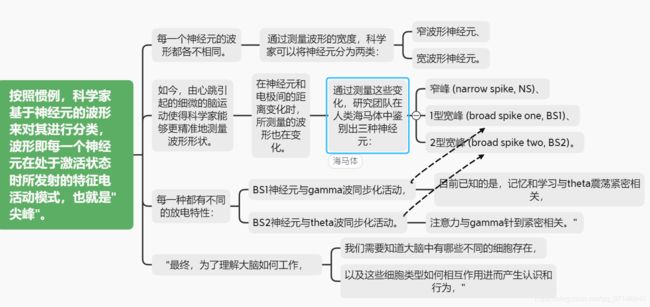
In humans and nonhuman primates, the classification of putative inhibitory interneurons and excitatory pyramidal cells is often based on the width of the EAP waveform. Units with broad spiking (BS) waveforms are classified as pyramidal cells, while units with narrow spiking (NS) waveforms are classified as interneurons (Barthó et al., 2004, Connors and Gutnick, 1990, Markram et al., 2004, McCormick et al., 1985, Peyrache et al., 2012, Rao et al., 1999, Sirota et al., 2008, Wilson, 1994). NS and BS waveforms have been directly linked to these two classes in some instances using intra- or juxtacellular monitoring in rodents and monkeys (González-Burgos et al., 2019, Joshi and Hawken, 2006, Krimer et al., 2005, McCormick et al., 1985), cross-correlation of spike trains to reveal monosynaptic excitatory and inhibitory connections (Barthó et al., 2004, Mendoza et al., 2016, Peyrache et al., 2012, Tamura et al., 2004), and antidromic electrical stimulation to identify excitatory projection neurons (Johnston et al., 2009). Importantly, in vivo recordings throughout the brain reveal that groups of neurons with NS or BS EAPs play functionally distinct roles in behavior (Anastassiou et al., 2015, Ison et al., 2011, Mitchell et al., 2007, Oemisch et al., 2015, Peyrache et al., 2012, Peyrache and Destexhe, 2019, Rutishauser et al., 2015, Takahashi et al., 2015, Trainito et al., 2019, Viskontas et al., 2007). Nevertheless, the assumption that all NS cells are inhibitory and all BS cells are excitatory is not always true: some excitatory cells elicit narrow spikes and some inhibitory cells elicit wider spikes (Freund and Buzsáki, 1996, Gray and McCormick, 1996, Onorato et al., 2020, Vigneswaran et al., 2011, Gouwens et al., 2019). Apart from the procedures outlined above (which are often impractical or impossible to perform in human recordings), we lack a method for relating EAPs to the spectrum of cell types identified and predicted by genetics, morphology, and electrophysiology in humans and in monkeys. While several studies have identified EAP clusters beyond NS and BS types in primates and have demonstrated distinct functional roles for these different classes (Ardid et al., 2015, Onorato et al., 2020, Trainito et al., 2019), as yet we are unable to link these putative cell classes to the cell types recognized based on slice electrophysiology and predicted by genetics.
One reason it is difficult to assign cellular identity using features of the average EAP is that the EAP does not directly reflect the intracellular action potential waveform (Anastassiou et al., 2015). In fact, the EAP waveform reflects details of the recording electrode (dimension, material; Nelson and Pouget, 2012), properties of the extracellular space (distance to neuron, conductance Logothetis et al., 2007, Anastassiou et al., 2015), the cellular morphology (e.g., Gold et al., 2006, Hunt et al., 2019), the ionic composition of the cell, and other aspects such as brain state (Buzsáki et al., 1996). As the recording electrode moves farther away from the cell body of a neuron, the EAP width increases (Gold et al., 2007), so that the same neuron, recorded at different distances, can appear to elicit a range of narrow and broad EAP widths (Pettersen and Einevoll, 2008). By considering how the EAP varies at multiple locations around a cell with high-density electrodes in rodents, cell types beyond the NS versus BS distinction can be identified in the awake behaving animal (Jia et al., 2019). In the human brain, there is a disconnect between the number of morphological and genetically distinct neural subtypes (Aevermann et al., 2018, DeFelipe et al., 2013, Hodge et al., 2018) (the adult rodent neocortex is estimated to consist of more than 100; Tasic et al., 2018), and the types we are able to differentiate in vivo based on distinctive EAP properties. Moreover, it has been inherently difficult to interpret distinguishing EAP properties (beyond width) and link them to known intracellular features of neural types.
In many experimental paradigms, especially in humans with chronic implants, recordings are restricted to electrodes for which the activity of a neuron is detectable only on a single channel (e.g., on a microwire or a single shank of the Utah array). To improve the spatial sampling using only a single channel, one option in acute paradigms is to drive the electrode in small steps and record from the same neuron at several locations. Another possibility in both acute and chronic recordings is to take advantage of the motion produced through inherent physiological mechanisms, e.g., pulsatile motion of the brain caused by rhythmic changes in intracranial pressure during the heartbeat. While typically perceived as an unwanted effect that compromises data collection (Chen et al., 2012, Fee, 2000, Srivastava et al., 2005), here we propose that periodic, heartbeat-related motion improves the spatial sampling of the extracellular space. Just as high-density recordings improve unit classification compared to microwire recordings, this periodic sampling offers insights into the spatiotemporal variability of EAP features, which, in turn, can be linked to distinct, cell-class-dependent properties.
Results
The EAP Waveform Is Modulated by Cardiac Motion
During the heartbeat, the intracranial pressure changes. We hypothesize that this causes electrodes to move (Figure 1A). If an electrode moves during a cardiac pressure wave, then the EAP will be recorded at different locations around a cell (Figure 1B). In this study, we monitored the heartbeat (electrocardiogram [EKG]) and isolated 1,090 single units from 31 awake behaving humans across 47 recording sessions. We recorded neurons from both subcortical (hippocampus [HIPP], amygdala [AMY], putamen [PUT], substantia nigra [SN], subthalamic nucleus [STN]) and cortical structures (orbitofrontal cortex [OFC], anterior cingulate cortex [ACC], pre-supplementary motor area [pre-SMA]) (Figures 1C and S1A; Tables S1 and S2).
Figure thumbnail gr1
Figure 1Extracellular Action Potential Waveforms in the Human Brain Are Modulated by the Cardiac Cycle
Show full caption
View Large ImageFigure ViewerDownload Hi-res imageDownload (PPT)
We quantified four features of the EAP waveform: amplitude (AMP), half-width (HW), trough-to-peak width (TPW), and repolarization time (REP; Figure 1D). We calculated these “standard” EAP features for the mean EAP of each unit. We also aligned the single-unit spike times to the R-wave of the EKG, i.e., the prominent peak that denotes ventricular depolarization and muscular contraction that initiates the cardiac cycle. Through spike-R-wave alignment, we observed that EAP features of the same unit varied consistently and periodically as a function of the cardiac cycle (Figure 1E). For example, some units exhibited an increase in EAP AMP toward the end of the cardiac cycle with a concomitant decrease in EAP HW (Figure 1E, left panel) while others exhibited the inverse response (Figure 1E, middle panel)
To quantify the periodic variation of each feature during the cardiac cycle, we calculated a motion index (MI, see STAR Methods, e.g., an MI = 5.0 indicates that the feature increases by 5% during the cardiac cycle). On average, the EAP AMP varied 1.7% +/- 0.78% throughout the brain, with the strongest modulations in deep-brain structures (Figure 1F, AMP MI of deep subcortical structures: AMY = 2.6, HIPP = 2.3, PUT = 1.7, SN = 1.9, STN = 2.7 versus cortex: ACC = 0.9, OFC = 0.88, pre-SMA = 0.8). Across all neurons recorded in a brain area, the EAP was significantly modulated by the cardiac cycle in HIPP, AMY, PUT, STN, and SN (p = 1.9 × 10–12, 0, 0.031, 0.025, 0.0003) but not in ACC, OFC, or pre-SMA (p = 0.147, 0.269, 0.115). The average AMP MI in subcortical structures was significantly higher than in cortex, suggesting that brain motion associated with the cardiac R-wave is stronger in deep-brain structures (subcortical = 2.24 +/- 0.44, cortex = 0.87 +/- 0.04; t test, t(6) = 5.189, p = 0.002).
EAP features covary with distance from the recording electrode, e.g., with increasing distance between electrode and cell body, dendritic currents give rise to an increase in EAP HW as the AMP decreases (Anastassiou et al., 2015, Gold et al., 2006, Pettersen and Einevoll, 2008). We captured these dependencies by calculating a motion correlation (MC) metric between each EAP feature and AMP (see STAR Methods). This metric shows, for example, that AMP and HW were often anticorrelated with an MC of −0.15 ± 0.45 HW/AMP across all cells (mean ± SD); i.e., if AMP decreases by 10%, HW increases by 1.5%. Across the population, we found that HW negatively correlated with AMP (HW and AMP were linearly correlated for each neuron, and these correlation coefficients exceeded zero for the population; t test, t(1089) = −11.6, p = < 0.0001).
Variability in EAP Features during Cardiac Motion Reveals Three Cell Classes in the Human HIPP: NS, BS1, and BS2
Given that the motion-related effect on EAP waveforms is abundant in deep-brain structures, we next focused our analyses on the HIPP, a deep-brain region where, in rodents, numerous excitatory and inhibitory neural classes have been identified (Freund and Buzsáki, 1996; Graves et al., 2012, Hunt et al., 2018, Klausberger et al., 2003, Harris et al., 2018). We applied our analysis to the 69 units exhibiting the strongest cardiac-related AMP MI (the subset of cells with the strongest AMP modulation during the cardiac cycle, mean AMP MI = 4.1 ± 3.1; this subset was selected by comparing the EAP of an individual cell to the bootstrap shuffled waveforms at p < 0.05, STAR Methods). Although the remaining 114 hippocampal units had comparably weaker AMP MI (1.1 ± 0.7), these more weakly modulated units still exhibited statistically significant modulation as a group (t test, t(113) = 2.14, p = 0.03). In later parts of the paper (Figure 7), we apply the methods developed from the robust group of modulated neurons to the entire group of hippocampal units.
We clustered the EAP features of these 69 units in two ways: using standard features and with the inclusion of motion features. Standard features delineated units with narrow and broad EAP widths (Figures 2A and 2B ; Figures S2A and S2B), henceforth, referred to as NS and BS units (comparison of width between NS and BS cells, respectively: HW = 0.225 ± 0.020 ms versus 0.272 ± 0.025 ms, rank sum p = 1.02 × 10−7; TPW = 0.348 ± 0.150 ms versus 0.740 ± 0.127 ms, p = 1.8 × 10−8; REP = 0.226 ± 0.140 ms versus 0.447 ± 0.070 ms, p = 1.5 × 10−7). Interestingly, a bimodal distribution of NS and BS cells was observed across different brain areas (see violin plots Figure S1B). The Hartigan’s dip test of multimodality indicates that TPW (the most common metric used to distinguish NS and BS cells in humans and nonhuman primates) is significantly multimodal in ACC (p = 0.048), pre-SMA (p = 0.0001), and HIPP (p < 0.0001). Similarly, the distribution of TPW values is better explained by a mixture of two Gaussian distributions (bimodal) than a single Gaussian (unimodal) in ACC, AMY, HIPP, OFC, and pre-SMA.
Figure thumbnail gr2
Figure 2Motion Features Identify Three EAP Clusters in Human HIPP (NS, BS1, and BS2)
Show full caption
View Large ImageFigure ViewerDownload Hi-res imageDownload (PPT)
While the standard EAP feature set identified two clusters of EAPs, the feature set including motion features (MI and MC) revealed three. Motion features split BS units into two groups: BS1 and BS2 (Figure 2C). While BS1 and BS2 units share standard features, their motion-related features differ (Figures 2C and 2D; e.g., TPW is more strongly negatively correlated with AMP for BS2 cells than BS1 cells). Even though BS1 and BS2 units originate from the same BS population, BS1 versus BS2 cannot be distinguished from standard EAP features alone. The optimal number of clusters in the standard space is 2, indicated by minimizing the f(k) density function (Figure 2A). However, forcing these units to cluster into three groups in the absence of motion features did not result in the same BS1 and BS2 groups identified from the feature set accounting for motion (Figure S2C). Hierarchical clustering analysis illustrates that NS cells maintain their cluster labels in both the standard and motion feature sets, while BS units split into BS1 and BS2 only when utilizing motion features (Figure 2E). Of the 69 hippocampal units exhibiting the strongest EKG-related EAP variability, 18 were identified as NS (26%), 19 as BS1 (27%), and 32 as BS2 (46%).
It is possible that in some recording sessions the cardiac pulse is stronger, leading to greater electrode movement. We would expect this to be reflected in a greater EAP AMP MI. Among all three clusters, cardiac-related motion equally and significantly influenced the EAP AMP MI (t test of bootstrap Z-scored AMP MIs are different from zero, NS t(17) = 4.53, p = 0.00029; BS1 t(18) = 5.77, p = 0.000018; BS2 (t(31) = 6.80, p = 1.28 × 10–7; comparison of EAP AMP MI among cell types: ANOVA, F(66,2) = 1.84, p = 0.168). As a control, we assessed whether units belonging to different clusters were recorded simultaneously. Of 39 unique pairs of cells recorded on the same wire, 14 pairs (36%) were of different cell types (probability of recording each cell type simultaneously: p(NS and BS1) = 5%, p(NS and BS2) = 10%, p(BS1 and BS2) = 21%)). Of 269 unique pairs of cells recorded on the same bundle of wires on a hybrid electrode, 616 (55%), were pairs of different cell types (p(NS and BS1) = 9%, p(NS and BS2) = 9% p(BS1 and BS2) = 28%)). As BS1 and BS2 units can be recorded simultaneously on the same wires, it is unlikely that these reflect cell types from different regions of HIPP and, instead, are more likely to represent homogeneously dispersed cell types within a region (albeit, different regions of HIPP could have these cell types in different proportions).
While we largely focus on the HIPP we also tested our methodology in the AMY and STN, two brain areas with units exhibiting significant modulation in EAP AMP during the cardiac cycle (Figure 1F). Clustering with motion features revealed additional groupings in the AMY (Figure S3), a structure known for its plethora of distinct cell types (Millhouse and DeOlmos, 1983, Spampanato et al., 2011, Washburn and Moises, 1992). In contrast, we found no additional clusters in the STN (Figure S4), a structure that has a relatively homogeneous cytoarchitecture consisting largely of projection neurons (Yelnik and Percheron, 1979). Hence, large cardiac-related modulation in EAP features does not necessitate more unit clusters.
Biophysically Realistic Simulations Estimate the Cardiac-Related Motion at About 3 μm
We employed biophysically realistic single-neuron simulations of 10 spiny (SP) and 4 aspiny (AP) human neurons to understand how cardiac-related motion influences EAPs (Figure 3A). The three-stage optimization workflow to fit the biophysical models (Figure 3B) relies on two data modalities: the reconstructed morphology and the somatic electrophysiology responses from whole-cell patch-clamp experiments (Figure 3C; see STAR Methods). The multi-objective optimization procedure aims to minimize the sum of objectives (somatic electrophysiology features) resulting in the fit of a set of ionic conductances (free parameters; Figures 3D–3F). The outcome of this procedure are conductance-based single-neuron models reflecting in vitro, whole-cell patch-clamp recordings from cortical neurons obtained from tissue resected from the human temporal and frontal lobe of 11 patients (Table S3). The models capture the intracellular dynamics during spiking and offer the ability to simulate the EAP (Anastassiou et al., 2015, Gold et al., 2007, Gold et al., 2006, Jun et al., 2017, Schomburg et al., 2012, Taxidis et al., 2015).
Figure thumbnail gr3
Figure 3Optimization Workflow for Single-Cell All-Active Models of Human Cortical Neurons
Show full caption
View Large ImageFigure ViewerDownload Hi-res imageDownload (PPT)
We simulated cardiac-related motion in these models through “virtual” extracellular recordings. We selected a location (“recording electrode”) within 100 μm from the soma of the model neuron and moved the location of this electrode to emulate the relative motion during the EKG period. Examples of simulations are shown for two models, one AP (Figure 4A) and one SP (Figure 4B). The modulation of EAP features during the simulated motion is qualitatively similar to in vivo recordings (e.g., compare Figures 4A and 4B to Figure 1E). We calculated the standard and motion-related EAP features for each model for 1–20 μm of simulated electrode motion. Figure 4C illustrates the feature space for 3 μm of relative motion (range selected for EAPs AMP-matched to those observed in vivo; 43.4 ± 24.8 μV). We compared the AMP and AMP MI modulation of our in vivo recordings to the model predictions and estimate that the microwires in our in vivo recordings are about 31.2 ± 15.6 μm away from the cell body (Figure 4D top) and transverse a relative distance of 3.45 ± 3.07 μm during the cardiac cycle (Figure 4D bottom).
Figure thumbnail gr4
Figure 4Simulated Electrode Motion in All-Active, Biophysically Realistic Models of Human Neurons
Show full caption
View Large ImageFigure ViewerDownload Hi-res imageDownload (PPT)
Classifiers Indicate that NS Cells Are AP Neurons, while BS Cells Are SP
It remains unknown whether and how the recorded hippocampal units map onto cells of distinct types at the morphological or genetic level. We hypothesized that the properties of cells recorded in vivo could be predicted by mapping their EAP data into the model feature space, where we know both the morphological and electrophysiological cell type and can produce a simulated EAP signature. These models offer an ideal tool to test whether EAP features alone can differentiate between distinct (and known) cell types – if successful, these classifiers can be then applied on experimental EAP waveforms. To do so we implemented two approaches: (1) an experiment-based approach, and (2) a simulation-based approach.
In the experiment-based approach, we trained classifiers using the experimental EAP data and their associated EAP cluster labels, NS and BS (Figure 2). We then used these classifiers to predict the morphological type of the model neurons, AP and SP, solely based on EAP properties (see STAR Methods). We compared classifiers trained on different combinations of EAP features: (1) only standard EAP features, (2) standard + MI features, (3) standard + MI + MC features, and (4) only MI + MC features. Figure 5A shows the performance accuracy on experimental data left out in training. Confusion matrices indicate that standard features are required and sufficient to differentiate NS from BS units. Indeed, classifiers with standard features (S) perform as well as classifiers with motion features included (S + MI + MC) (cf. Figure 5A, S to S + MI + MC). Confirming this result, the beta coefficients of the dividing plane used by the classifier are high for standard EAP features, indicating their significant contribution to the separation between NS and BS units (i.e., TPW, HW, REP; Figure 5B). When applying this classifier (trained on the standard experimental feature space) to the EAP feature space of the single-cell models, AP units were robustly classified as NS cells and SP units as BS cells, respectively (Figure 5C). This shows that a classifier trained on experimental data generalizes successfully to the model data.
Figure thumbnail gr5
Figure 5In Vivo NS and BS Units Map onto Single-Cell SP and AP Models
Show full caption
View Large ImageFigure ViewerDownload Hi-res imageDownload (PPT)
In the simulation-based approach, we trained classifiers on the model EAP data using the ground truth label determined from the reconstructed morphologies of the human neurons (SP or AP; label based on morphological presence or absence of dendritic spines). The classifier that used standard features discriminated model AP and SP neurons with 84% accuracy (Figure 5D). We tested this simulation-based classifier on the experimentally recorded, hippocampal EAP waveforms. The majority (17/18, 94%) of neurons labeled experimentally as NS were classified as model AP neurons, while the majority (46/51, 90%) of neurons labeled BS were classified as SP. Thus, the simulation-based classifier, like the experiment-based classifier, robustly generalizes across feature spaces and attributes NS waveforms to AP neurons and BS waveforms to SP neurons.
Intrinsic Electrophysiological Properties of BS1 versus BS2 Neurons
Our analysis of motion-related EAP features indicates the presence of two BS classes, BS1 and BS2 (Figure 2C). What differentiates BS1 from BS2 units? To characterize the properties of BS1 versus BS2, we used simulation- and experiment-based approaches as above.
In the simulation-based approach, we “recorded” the EAP at 25 random locations around each human neuron model, simulating 3 μm of motion (i.e., the average motion estimated in Figure 4D; 10 model SP neurons were used from 8 patients). Cluster analysis on the EAP features of the SP models resulted in two groups: SP1 and SP2 (Figures 6A and 6B ). The motion-related features of the two clusters shared many similarities with those of BS1 and BS2 units recorded in vivo, e.g., B2 and SP2 exhibit strong negative correlations between HW/TPW and AMP (cf. Figures 2D and 6B, HW MC or TPW MC). While some model neurons (e.g., model #5, Figure 6C) exclusively gave rise to EAPs belonging to a single SP waveform cluster (in this case SP1), most models had EAPs in both clusters (e.g., 70% of the EAPs for model #1 belong to the SP1 cluster and 30% belong to the SP2 cluster). This lack of one-to-one mapping of EAP cluster-labels to each model occurs because the same neuron can elicit a spectrum of EAP waveforms, depending on the proximity of the recording electrode to the soma and dendrites (Gold et al., 2006). Mirroring the random location of extracellular recording locations in humans, we chose to label a model neuron as SP1 (or SP2) if the majority of its EAPs (>13/25 EAPs) belonged to the SP1 (or SP2) cluster. We identified 4 neurons as SP1 and the remaining 6 as SP2. We trained classifiers with these labels to identify model EAP waveforms as SP1 or SP2 (Figure S5). The classifier that utilized motion-based features performed with 20% higher accuracy on left-out test data than the classifier based on standard features alone (41% versus 62% respectively, Figure S5). These data illustrate that relative motion can uncover EAP features unique to individual classes and thereby facilitate classification of model cells.
Figure thumbnail gr6
Figure 6Two Types of Hippocampal Broad-Spike Waveform Cells (BS1 and BS2) Are Identified In Vivo
Show full caption
View Large ImageFigure ViewerDownload Hi-res imageDownload (PPT)
In the experiment-based approach, we trained classifiers on the in vivo data using the BS1 versus BS2 cluster labels (Figure 2C) and a variety of EAP feature sets. Motion-related features supported the separation of BS1 and BS2 classes: classifiers using these features performed better (84% accuracy) compared to the classifier solely trained on standard features (60% accuracy; Figure 6D). Can classifiers trained exclusively on experimental EAP data predict the label of single-cell models? We applied the experimental-based BS1-BS2 classifier (including MC and MI features) to the SP-BS simulated EAP data and revealed that six model SP neurons are robustly identified as BS2, while the remaining four are classified as BS1 (Figure 6E).
Both the model- and experiment-based approach converge on the same result: BS1 and BS2 EAPs originate from two classes of neurons, namely, SP1 and SP2 (Figure 6F; the majority of BS1 and BS2 neurons are labeled as SP1 and SP2 both by the model- and experiment-based classifier). Yet, what is unique about the cellular properties of BS1-SP1 versus BS2-SP2 neurons that leads to such EAP feature- and motion-based separation? We analyzed multiple intracellular electrophysiological features (e.g., input resistance, firing rate) from the in vitro patch-clamp experiments each single-cell model was generated on. We found that SP2-BS2 cells exhibit a higher mean rheobase current, a lower input resistance, a longer spike ramp time, and lower membrane time constant compared to their SP1-BS1 counterparts (Figure 6G). Intriguingly, these 4 features account for the largest variance in the intrinsic feature space and together map onto the first component in PCA space (Figure 6H, scores of PC1 are significantly different for BS1-SP1 and BS2-SP2 cell types, t test, p = 0.01). This shows that the split of the BS class into BS1 and BS2 sub-classes is not arbitrary but maps onto neural classes with distinct intracellular features. Importantly, these intrinsic cellular properties cannot be measured directly in vivo in humans and are only accessible by bridging across data modalities, in our case via biophysically detailed modeling.
NS, BS1, and BS2 Cells Have Distinct In Vivo Properties during Endogenous Oscillations
Functionally distinct cell types uniquely coordinate their spikes to other classes and/or with respect to endogenous rhythms measured by the local field potential (LFP) (e.g., Klausberger et al., 2003, Klausberger and Somogyi, 2008). To pursue functional classification of human hippocampal NS, BS1, and BS2 neurons, we compared their in vivo spiking characteristics. We classified the entire population of 183 recorded hippocampal cells (i.e., this analysis is not restricted to only the strongly modulated cells) in a hierarchical fashion: by first applying the NS versus BS experiment-based classifier (Figure 5A) and then the BS1 versus BS2 model-based classifier (Figure 6D) to units identified as BS. Of the total population of 183 recorded hippocampal neurons, 49 were identified by the experimental classifier as NS (27%), 53 as BS1 (29%), and 81 as BS2 (44%). As with the original subset of 69 strongly modulated units, in this expanded set units of different cell classes were recorded by the same wire or wire bundle suggesting they are members of truly distinct cell types (72/145, 49%, unique pairs on same wire are of different cell types; 616/1,112, 55%, of pairs on same bundle are from different cell types; percentage of unique pairs that are BS1 and BS2 pairs, p(BS1 and BS2 same wire) = 27%, p(BS1 and BS2 same bundle) = 33%). NS, BS1, and BS2 units in the human HIPP exhibited similar low spike rates (NS: 1.6 ± 1.1 Hz, BS1: 1.2 ± 0.31 Hz, BS2: 1.4 ± 1.1 Hz, mean ± SD, ANOVA F(2,176) = 0.47, p = 0.625) with only 13/183 hippocampal cells (7%, 3 NS, 2 BS1, 8 BS2) having a mean rate that exceeded 10 Hz. Low spike rates are typical for human hippocampal (Rutishauser et al., 2008, Viskontas et al., 2007) and neocortical cells (Peyrache et al., 2012). BS1 and BS2 cells exhibit higher variability in their spike rates than NS cells (Figure 7A ). Autocorrelograms indicate that this variability in spike rate is due in part to transient bursts of increased spiking activity of, on average, relatively quiescent cells (Figure 7A, burst index, Figure 7B). As a population, BS1 and BS2 cells are burstier than NS cells, which, in turn, exhibit uniform spike times (Figure 7B, bar plot; 57% of BS1 and BS2 cells are bursty compared to 35% of NS cells [bursty/not bursty × NS/BS, chi-square(1) = 6.56, p = 0.0104]; 22% of BS1 and BS2 cells fire with uniform rates compared to 51% of NS cells [uniform/not uniform × NS/BS, chi-square(1) = 12.66, p = 0.0004]).
Figure thumbnail gr7
Figure 7NS, BS1, and BS2 Cells in the Human HIPP Exhibit Distinct Spike Patterns and Phase Coupling Properties In Vivo
Show full caption
View Large ImageFigure ViewerDownload Hi-res imageDownload (PPT)
We quantified spike-LFP synchrony with two measures: spike field coherence (SFC) and the Von Mises kappa value, an estimate of spike phase concentration. Human HIPP neurons exhibit a high propensity to synchronize their spiking to local theta (Figures 7C–7E; 34% of the n = 992 unit-LFP pairs show significant phase concentrations as assessed by their kappa values; Figure 7E average of three bars with theta label). BS2 neurons are more likely to synchronize to local theta than BS1 or NS neurons (BS2 = 42%, NS = 28% and BS1 = 29%; Figure 7E), while BS1 cells exhibit enhanced coupling with low and high gamma oscillations (i.e., 43% BS1 cells fire at high gamma versus 19% BS2 and 18% NS). Furthermore, BS1 and BS2 are more likely to entrain to beta than NS (Figure 7E). Note that for the spike-field analysis we chose pairs of units and LFPs recorded on different neighboring electrodes; this ensures that the observed spike-field relationships remain unaffected by the EAP of a recorded unit contaminating low-frequency currents in the LFP (Anastassiou et al., 2015, Schomburg et al., 2012, Zanos et al., 2012). As an additional control, we repeated the analysis using only the subset of units from microwire bundles in which all three types were simultaneously recorded (n = 8 recording sessions, 115 cells) and observed similar effects (Figure S6). The differences in spike-field synchronization between cell types cannot be explained by differences in LFP. Indeed, across the population, the spike-triggered power is similar among different neuron types (Figure S6C).
We conclude that NS, BS1, and BS2 are distinct cell classes in the human HIPP that differ in their EAP waveform, their putative intrinsic properties, and their unique coupling characteristics to ongoing and functionally relevant hippocampal LFP oscillations. Importantly, the functional characteristics were not a priori included in the identification of these classes. Instead, they resulted as an unbiased prediction of the waveform-based classification that linked in vivo recordings to models with known intrinsic cellular properties.
Discussion
We found that the EAP waveforms of neurons recorded with extracellular wires in the human brain in vivo exhibit small but robust and temporally periodic feature modulation during the cardiac cycle. This modulation occurs throughout the brain, with the strongest effects in deep-brain structures. These deep structures may be more susceptible to cardiac motion because of the dense bed of arteries at the base of the brain (Terem et al., 2018). While changes in EAP features due to cardiac-related motion have not been systematically documented in the human brain, cardioballistic motion effects are prominent in other electrophysiological and imaging techniques (e.g., EEG, [Srivastava et al., 2005], calcium imaging [Chen et al., 2012], functional imaging [Terem et al., 2018]). We show through biophysical simulations of human cortical neurons that a relative displacement of ~3 μm can account for the experimentally observed EAP waveform jitter. This estimate complements predictions of functional imaging in humans that estimate cardiac motion to be ~50 μm or less (Terem et al., 2018). The simulations also indicate that the distance between a neuron and a recording electrode is approximately 20–30 μm, an estimate in agreement with in vitro experiments (Anastassiou et al., 2015) and computational modeling (Gold et al., 2007, Gold et al., 2006, Taxidis et al., 2015). Although the estimated recording distance suggests a relatively narrow radius for isolating single units in vivo (~30 μm radius around the soma, scarcely twice the radius of most microwires), within this region the features of the EAP vary substantially. For example, within the 30 μm radius of a soma, the majority of EAPs exhibit an inverse relationship between EAP AMP and width features, an observation predicted by modeling data that can be explained by the active propagation of action potentials (Pettersen and Einevoll, 2008, Anastassiou et al., 2015, Gold et al., 2007, Gold et al., 2006).
We identified BS1 and BS2 cells by capitalizing on motion features caused by the heartbeat, but in principle the same classification could be achieved by intentionally introducing small amounts of motion in the brains of humans or other species (e.g., by micro-manipulating acute recording electrodes in cortex of rats or the archistriatum of zebra finches; Fee, 2000). We further predict that other bodily rhythms modulating intracranial pressure (e.g., the respiratory cycle) could be used to quantify motion-related changes in the EAP to identify novel cell classes. Given the recent interest in how rhythms of the body (respiratory, gastric, cardiac, circadian) modulate neural activity and cognition (e.g., Heck et al., 2017, Tort et al., 2018, Zelano et al., 2016, Kern et al., 2013, Kim et al., 2019, Pedemonte et al., 2003), a future set of experiments will need to carefully characterize how bodily rhythms influence EAP waveforms, spike detection, spike sorting, and the resulting cell classification.
We defined three classes based on EAP features, NS, BS1, and BS2, that also differ in their in vivo spike characteristics as well as their predicted intrinsic cellular properties. The narrow-width EAP waveform and decreased spike rate variability of NS units (robustly classified in our analysis as AP neurons) is strongly reminiscent of inhibitory interneurons and basket cells (e.g., Barthó et al., 2004, Joshi and Hawken, 2006, Krimer et al., 2005, McCormick et al., 1985, Gouwens et al., 2019, Anastassiou et al., 2015). But what about the differences between BS classes, BS1 versus BS2? The inverse relationship between rheobase versus input resistance and ramp time points to BS1 neurons being electrotonically more compact than BS2. BS1 neurons also possess a considerably increased (i.e., roughly double) membrane time constant over their BS2 counterparts, suggesting they are more responsive to fast oscillatory input (Eyal et al., 2016; Koch, 2004), an observation also supported by the spike-field analysis (see below). The lower membrane time constant of BS2 neurons allows their membrane potential to be more easily entrained by slower synaptic input. BS1 versus BS2 EAP waveforms are indistinguishable when considering standard EAP features (but, crucially, are separable by their motion-related EAP features) suggesting that their short-term spike dynamics are supported by similar mechanisms (i.e., transient Na+ and K+ currents that shape the AP waveform in the ~2 ms window discernable by extracellular recordings are indistinguishable in the two BS classes). Slower K+ and Ca2±dependent conductances affect slower components of the EAP waveform and contribute to slower spike-related mechanisms such as adaptation (Anastassiou et al., 2015).
We find that AP NS units are entrained to a broad range of frequencies (from theta to high gamma), indicative of general inhibition (Fellous et al., 2001, Hasenstaub et al., 2005), whereas BS2 cells phase lock preferably to slower theta and alpha rhythms and BS1 cells preferably entrain to faster gamma oscillations. Such cell-class-specific entrainment is consistent with the intrinsic properties of the two classes. While the electrotonic compactness of BS1 cells renders them ideal for integrating faster synaptic drive, the increased membrane time constant of BS2 cells makes them more susceptible to slower synaptic drive (notably, in our work the intrinsic properties of BS classes are determined independently from phase-locking characteristics). Continuous rhythmic firing units versus clustered rhythmically firing units covering the theta band have been reported in human HIPP and are reminiscent of BS1- versus BS2-type activity (Isokawa-Akesson et al., 1987).
A possible limitation in ascribing specific intrinsic properties to BS1 versus BS2 neurons such as input resistance and rheobase is the use of neuron models derived from human neocortex rather than HIPP. The main challenge is the lack of morphological and electrophysiological single-neuron data from human single neurons from identified brain regions beyond human neocortex to allow the development of biophysically faithful and region-specific single-neuron models. Even so, we assess this limitation as relatively inconsequential toward our conclusions. Specifically, separation of BS in vivo units into BS1 versus BS2 in our work can be solely achieved based on feature modulation and does not depend on identifying intrinsic properties of each cell type. Yet, the fact that conclusions derived separately from the experimental- and simulation-based approach such as BS1 versus BS2 and SP1 versus SP2 cluster compositions are in such close agreement offers confidence in the model-based predictions. Regarding the estimation of intrinsic properties, while in rodents pyramidal neurons can exhibit differences, they also share many properties like an extended dendritic morphology, spike generation, and support mechanisms along their cables (Spruston, 2008), and distinct molecular markers (e.g., calcium/calmodulin-dependent protein kinase, which is present in both hippocampal and neocortical pyramidal cells ([Erondu and Kennedy, 1985]). We expect EAP features captured by the human neocortical models to be a reflection of these shared commonalities, while dissection of even finer, region-specific cell-type-differences requires a dedicated set of in vitro experiments and effort toward specific model development.
Our analysis focuses on four EAP waveform metrics (AMP, HW, TPW, and REP), because (1) they are general standards for cell classification in the in vivo literature, and (2) the use of these features allows for a common feature space between the model and in vivo data. We encountered several challenges in relating the model and experimental-feature spaces, e.g., matching the recording filters in the model with those of the in vivo hardware and software, applying the same feature detection methods to both model and in vivo data, accounting for the impact of inherent background noise in the in vivo data that is absent in the modeling data. Because our models are based on reconstructions of in vitro recordings, we optimized not only the spiking properties of the cell model (spike timing, spike rate) given a particular morphology but also the intracellular action potential waveform, especially the EAP AMP and HW. Indeed, because HW is included in the optimization workflow and strongly matches the in vitro recordings, it is a major feature in discriminating cell classes in both the model and experimental space (Figure 5E).
While here we focus on the human HIPP, our overall approach is applicable to other brain areas and other species where EAPs are jittered by relative motion; in the case of cardiac motion we showed evidence in other deep structures like the AMY and STN. Furthermore, we showed how biophysical models can be used to link to seemingly dissociated datasets (in vitro physiology and morphology reconstructions with in vivo recordings of unit activity and LFPs) to offer insights into the identity and unique properties of recorded neurons. We view this approach as a promising means toward data reconciliation, cell classification, and functional interpretation particularly in human brain circuits where most of the multi-modal experimentation attainable in animal models remains unfeasible.
STAR★Methods
Key Resources Table
REAGENT or RESOURCE SOURCE IDENTIFIER
Software and Algorithms
MATLAB 2017b MathWorks RRID: SCR_001622
Python Python.org RRID: SCR_008394
Neuron 7.5 Simulator NEURON RRID: SCR_005393
OSort cell sorting algorithm Rutishauser et al., 2006 RRID: SCR_015869 https://rutishauserlab.org/osort/
Allen Institute Brain Modeling kit Allen Institute for Brain Science https://github.com/AllenInstitute/bmtk
Human cells for in vitro recordings Allen Institute for Brain Science https://celltypes.brain-map.org/
Blue Brain optimization (BluePyOpt) Blue Brain Project https://github.com/BlueBrain/eFEL
QRS Tool Allen et al., 2007 https://jallen.faculty.arizona.edu/content/qrstool-and-cmetx-software-calculating-metrics-cardiac-variability
Dataset of human medial temporal lobe single neuron activity during declarative memory encoding and recognition Faraut et al., 2018 https://datadryad.org/stash/dataset/doi:10.5061/dryad.46st5
Cardiac-motion EAP Cell Classifier This manuscript https://github.com/rutishauserlab/cellclassifier
Human all active models This manuscript https://github.com/AllenInstitute/Human_all_active_models_EAP
Other
Neuralynx Neurophysiology System Neuralynx Cat# ATLAS 128
Spencer SEEG electrodes Ad-Tech Medical RD06R-SP05X-000
Behnke-Fried Hybrid electrodes Ad-Tech Medical BF08R-SP05X- WB09R-SP00X-0B6
Alpha Omega MicroGuide System Alpha Omega Cat# STR-000021
Alpha Omege Hybrid Microelectrodes Alpha Omega Cat#IS08RSP10X-0T1
Open table in a new tab
Lead Contact and Materials Availability
Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Ueli Rutishauser ([email protected]). The spike-time data from the in-vivo recordings in epilepsy patients, the EAP waveform classifiers, the in vitro recordings used to generate the single-neuron models, and the all active human single neuron models are available publicly for download (see Key Resources Table). This study did not generate new unique reagents.
Experimental Model and Subject Details
A total of 31patients volunteered to participate in the in vivo experimental recordings (see Tables S1 and S2 for age and gender). All subjects gave informed consent and all protocols were approved by the Institutional Review Board of Cedars-Sinai Medical Center. Eleven patients were implanted with hybrid depth electrodes for monitoring the source of intractable epilepsy (for details, see Carlson et al., 2018, Rutishauser et al., 2010). In addition to these recordings, we recorded electrophysiological signals intraoperatively from 20 patients with motor disorders being implanted with deep brain stimulation (DBS) electrodes (for details, see Kamiński et al., 2018).
Model neurons were based on human neurons obtained from cortical tissue resected from 11 patients for the purpose of removing epileptogentic tissue (Table S3). Surgical specimens were obtained from local hospitals in collaboration with a network of neurosurgeons. All patients provided informed consent for tissue donation, and all experimental uses were approved by the respective hospital Institutional Review Board before commencing the study (for more details, see http://celltypes.brain-map.org/donors).
Method Details
In vivo neural recordings with cardiac monitoring
Eleven patients were implanted with hybrid electrodes for monitoring the source of intractable epilepsy (for details, see Rutishauser et al., 2010). Each electrode contained a bundle of 8 microwires for recording single unit activity and local field potentials. Electrodes targeted, bilaterally, the amygdala, hippocampus, anterior cingulate cortex, orbitofrontal cortex, and pre-supplementary motor area. The location of the electrodes was verified with post-operative T1-weighted structural MRI scans registered to an atlas in MNI152 space (Kamiński et al., 2017). Broadband (0.1 Hz to 9 kHz) electrophysiological signals were recorded postoperatively at a 32 kHz sampling rate using a 256-channel ATLAS system (Neuralynx, Bozeman MT). Signals were locally referenced to one of the eight microwires in the bundle.
In addition to these recordings, we recorded electrophysiological signals intraoperatively from 20 patients with motor disorders being implanted with DBS electrodes (for details, see Kamiński et al., 2018). During each intraoperative session, two microelectrodes were placed to map the transitions through different brain regions and to identify the target for the DBS electrode. Microelectrode recordings targeted the subthalamic nucleus, the substantia nigra, or the putamen. Target locations were determined stereotaxically based on preoperative 3T T1- and T2-weighted MRI scans co-registered with preoperative CT scans (Kamiński et al., 2018). Broadband (0.1 Hz to 32 kHz) electrophysiological signals were recorded intraoperatively at a 40 kHz sampling rate using a NeuroOmega system (Alpha Omega, Nazareth Il.). Signals were referenced to the cannula that delivered the microwire.
During neurophysiological recordings we simultaneously recorded the electrocardiogram (EKG) from two surface electrodes placed on the chest and referenced to the neck. EKG was sampled at 1 kHz and recorded and amplified through the headstages used to record LFP from the macro-contacts on the neurophysiological recording electrodes. EKG was filtered offline (3rd order FIR filter, 3-30 Hz bandpass) and the peak of the QRS wave was detected using the open-source software QRSTool (Allen et al., 2007). Interbeat intervals (IBIs) measured the time between subsequent R-waves in milliseconds.
All-active single-neuron models with motion simulation
In this paper, we constructed model neurons and simulated motion for 4 biophysically-realistic human cortical aspiny (AP) neurons and 10 spiny (SP) neurons obtained from cortical tissue resected from 11 patients for the purpose of removing epileptogentic tissue (Table S3). Each in vitro experiment resulted in a set of electrophysiology responses to standardized current injection protocols as well as a reconstructed morphology (both available online via https://celltypes.brain-map.org/).
Each human single-neuron model was generated based on a set of electrophysiological features (Figure 3). Moreover, since dendritic and somatic features of cell morphology affect various spatiotemporal characteristics of the EAP waveform, we accounted for the full dendritic reconstruction available for each neuron (Anastassiou et al., 2015, Gold et al., 2007, Gold et al., 2006, Holt and Koch, 1999, Jia et al., 2019, Pettersen and Einevoll, 2008). To capture the intricacies of the electrophysiological behavior of single-neurons and allow better convergence of the parameters, the model generation workflow was divided into three stages. At each stage, a new set of conductances (Na, K, and Ca dependent) were added to the reconstructed morphology and the relevant electrophysiological features were calculated from the experimental voltage traces using eFEL (https://github.com/BlueBrain/eFEL) - the conductance density for each conductance of a model is then fitted to replicate the experimental electrophysical features within a python based evolution algorithm toolbox BluePyOpt (Van Geit et al., 2016). This involves optimizing passive conductances along with capacitance, reversal potential and axial resistance in the initial stage with target features e.g., voltage deflection, steady state voltage being added to the multi-objective optimization program, followed by Ih conductances with features related to the voltage sag under hyperpolarizing current. Finally, the rest of the active conductances were added to the model to minimize errors between experimental and model spiking features such as action potential amplitude and width, interspike interval, spike adaptation index (see Figure 3 for illustration of optimization procedure).
After a single neuron model was optimized, we simulated the EAP using NEURON 7.5 simulator (https://www.neuron.yale.edu/neuron/) in combination with the Brain Modeling Toolkit (https://github.com/AllenInstitute/bmtk). This toolkit (Gratiy et al., 2018) is capable of simulating a variety of observables directly supported by NEURON (e.g., spikes, and membrane voltages), as well as plugging in modules for computing additional observations (e.g., the extracellular potential). The EAP traces were computed using the line-source approximation, which assumes that membrane current is uniformly distributed within individual computational compartments and that the medium is homogeneous and isotropic (Gratiy et al., 2018). The model was simulated at a sampling rate at 30kHz. The stimulation was a 23.44 ± 1.27 Hz Poisson-like synaptic input at 44 locations on the cell to elicit an average of 108+/- 52 SD spikes per model.
To account for the spatial extent of the recording electrode, we recorded the extracellular potential via the line-source approximation in a dense grid (1 μm spacing) consisting of 32 columns and 480 rows (total 14,400 recording channels). To faithfully account for the EAP waveform of an electrode spanning 32 × 32 μm2, we simulated the EAP in every location of the discretized mesh within this surface area. The final EAP waveform for the location at the center of the recording surface area was the average from the EAP waveform mesh. To mimic cardiac motion, we used a similar approach. Specifically, we simulated cardiac motion as a sinusoidal movement among adjacent recording channels during a 1Hz cycle. Figure 4A and 4B illustrate examples of 3 μm motion, in which the movement was among 4 recording channels sites during each cycle. At each recording site we simulated a variety of motion amounts (from 1 to 20 μm) to identify which amount of motion best estimated the motion observed experimentally. We estimated the motion and recording distance in our in vivo recordings by comparing in vivo values to the model data. For each EAP from an in vivo recorded unit we calculated the AMP and identify the location around every model with the same EAP AMP. In Figure 4D, therefore, each circle is one distance estimate (n = 69 in vivo hippocampal neurons x 14 models = 966 distance estimates total).
It follows that each single-cell model is linked to different datasets: on the one hand, the in vitro electrophysiology and reconstructed morphology datasets used to generate the conductance-based models in the first place and, on the other hand, the simulated EAP dataset, used to link a specific model to in vivo recorded units from human hippocampus. This link becomes particularly important as it allows EAP properties recorded from hippocampal units in vivo to be associated to morphological (aspiny versus spiny, Figure 5) and electrophysiological (Figures 6F–6H) in vitro properties of human single cells.
Quantification and Statistical Analysis
Spike detection and sorting of single units
The broadband signals from the in vivo recordings and the model neurons were filtered in the 300-3,000 Hz band using a zero-phase lag filter (four-pole Butterworth filter, see code release). The intracellular spiking activity of model neurons provided the spike times for the model EAP data. Spikes from in vivo recordings were detected and sorted using the semi-automated template-matching algorithm OSort (Rutishauser et al., 2006). We excluded channels with interictal epileptic activity. Each single unit was manually evaluated and verified based on a variety of features: (1) the spike waveform, (2) the percentage of interspike intervals (ISIs) less than 3 ms, (3) the ratio of the waveform extremum and the standard deviation of the noise, (4) the pairwise projection distance in the clustering space between all isolated neurons on the same microwire, (5) the coefficient of variation of the ISI and (6) the cluster isolation distance (Rutishauser et al., 2008). Of the 11 waveform features we used to cluster, three features (HW, TPW, and HW MC) were weakly but significantly correlated with isolation distance (R2 = 0.02, 0.11. 0.11, p = 0.016, 0.016, 0.16 respectively). The NS, BS1, and BS2 cells all had similar isolation distance, signal-to-noise ratio, and inter-spike interval (Figures S7A–S7C).
We recorded a total of 1,090 well-isolated neurons: 183 in hippocampus, 256 in amygdala, 148 in anterior cingulate, 145 in orbitofrontal cortex, 278 in pre-supplementary motor area, 14 in putamen, 35 in subthalamic nucleus, and 32 in substantia nigra.
Single unit firing properties and coherence with LFPs
Mean firing rate was calculated as the inverse of the mean of the interspike intervals during the recording session. Coefficient of variation (CV) is a measure of spike train variability and has a value equal to 1 for a Poisson process. CV was calculated as the standard deviation of the interspike interval divided by mean of the interspike interval. The local variation (LV) is similar to CV but measures variation in adjacent ISIs and was calculated according to Shinomoto et al., 2003.
Some neurons appear to have rate modulations during the cardiac cycle because the electrode motion influences spike detection and spike sorting. To quantify the degree of spike rate modulation we constructed raster plots and PSTHs of each cell aligned to the heartbeat (Figures S8A and S8B). The window began 20 ms before the heartbeat and ended when the median of that session’s interbeat interval had elapsed (median IBI, 804 ± 156 SD ms or 75 ± 15 beats per minute). We interpolated from 0 to 2π over this window to calculate the “phase” that each spike occurred relative to the heartbeat. The Rayleigh test of nonuniformity was applied to these spike-phases to determine if a cell’s firing rate was significantly modulated during the heartbeat (p < 0.01). In addition, we calculated 1,000 bootstrapped values for each neuron by randomly jittering the hearbeat times by up to 5 s and recalculating the spike rate at these jittered times. A cell was said to be significantly modulated by the heartbeat if the Rayleigh test-statistic was greater than 99% of these shuffled data and had a p value less than 0.01. In addition to calculating rate changes we also designed a metric to ascertain how well-isolated the spike sorting was at different time points in the cardiac cycle. First, we performed PCA on the EAP waveforms and calculated the Euclidean distance between each spike waveform and all other spikes in principal component space (using the components that explained 95% of the variance). Then, for each spike at a given time point in the cardiac cycle, we identified the 10 spike waveforms that were closest to it in EAP -PCA space and asked how many of these spikes were inside the same unit cluster and how many were outside the cluster. A value of 0 indicates the cell is well-isolated from other waveforms, while a value of 100% indicates that all of the nearest waveforms are outside the unit cluster (Figure S8E). We show that changes in spike rate during the cardiac cycle are likely due to missed detection of spikes outside the cluster, either because these spikes are assigned to a different cluster or fall into the background noise (Figure S8).
For each neuron we also calculated the autocorrelation function. Each spike train was represented as a binary vector and the autocorrelation was calculated with 500 ms lag using the xcorr function in MATLAB (functions available from MATLAB, all custom scripts for calculating EAP features and classifiers available for download in code release). Values were normalized to the zero lag value and are reported as spike rates. Similar to reports in the rodent hippocampus (e.g., Barthó et al., 2004 and other reports in the human hippocampus, e.g., Viskontas et al., 2007) we observed that the autocorrelation function could be characterized as three types of responses: regular-spiking cells that had a late peak > 20 ms, bursty cells with low-latency peaks < 20 ms, and cells that had a uniform distribution with no clear peak (Figure 7B). To quantify these three types of responses we first measured the median of the autocorrelation function and calculated the residuals of the autocorrelation function at 3-150 ms lag. If the residuals in this time window were homoscedastic (p > 0.05 Engle’s Arch test), the cell was identified as having a uniform autocorrelation with a rate equal to the median. If, however, the autocorrelation function failed the test of homoscedasticity then the maximum local peak in the autocorrelation function was detected. Cells with peaks that occurred at less than 20 ms were labeled as bursty cells, in line with other reports that cells in the human hippocampus burst with ISIs up to 20 ms in duration (Staba et al., 2002; illustrated as light shaded bars in Figure 7B). Because this metric does not account for the amount of time spent bursting, we also calculated an additional, stricter, burst metric: the summed magnitude in the 0-20 ms window of the time zero-scaled autocorrelogram, i.e., the probability that a spike will be followed by other spikes at a burst ISI latency. For the subset of neurons with a peak < 20 ms we also report the percent where this metric is greater than 0.05 (i.e., bursts more than 5% of the time, Figure 7B dark shaded bars). All other cells with peaks > 20 ms were labeled as regular spiking.
To determine if hippocampal cells entrained to local oscillations, we analyzed the LFP on each microwire relative to the spike time of each neuron. Broadband signals were first locally referenced to one of the 8 microwires that did not contain spiking activity and then low-pass filtered for frequencies < 300 Hz using a zero-lag FIR filter and down sampled to 1 kHz. Because the waveform of the EAP is known to significantly contaminate low-frequencies of the LFP (Anastassiou et al., 2015) we never compared LFPs and units recorded on the same microwire. We only compared LFPs to single units on different wires in the same bundle.
For each cell-LFP pair we first extracted 500 ms of the LFP signal before and after each spike. We chose such long windows because we were interested in frequencies as low as 3 Hz. Averaging these segments gives the spike triggered average (STA). We then estimated the frequency spectrum of the STA and of each spike-LFP segment using multitaper analysis with a time-bandwidth product of 7 and 3 tapers resulting in a frequency resolution of 3.5 Hz (Chronux toolbox). Spike filed coherence was then calculated by dividing the frequency spectrum of the STA by of the average frequency spectrum around each spike (Fries et al., 2001). We calculated the SFC for each neuron-LFP pair and observed a strong peak in the spike field coherence in the theta frequency band (3-8 Hz, Figure 7D) that appeared to differ for different cell classes. We then filtered the LFP in several frequency bands (theta = 3-8 Hz, alpha = 8-12.5 Hz, beta = 12.5-30 Hz, low gamma = 30-50 Hz, and high gamma 50-90 Hz) and estimated the phase of the analytic signal at each spike time using the Hilbert transform. To determine if a neuron exhibited a significant phase preference we applied the Rayleigh test for non-uniformity (p < 0.01) and also compared our phase-concentration metrics bootstrap shuffled data (see next paragraph). To quantify how strongly a neuron’s spikes were concentrated around a specific oscillatory phase, we estimated the kappa value of the Von Mises distribution (Circular Statistics Toolbox [Berens, 2009]). Kappa values range from 0 to 1 (though we have z-scored the values to shuffled data, see paragraph below). The reciprocal of Kappa is analogous to the variance of the normal distribution, i.e., higher kappa indicates a smaller variance in spike phase.
As previously noted, some cells appear to change their firing rate throughout the cardiac cycle because motion compromises spike sorting and detection (Figure S8). Since these rhythmic fluctuations in spike rate could potentially affect the SFC metric at low-frequencies near the heart rate (heart rate is about 1-2 Hz), we performed a necessary control: we compared all SFC and Kappa values to bootstrap shuffled data (Figure S9). For each neuron-LFP pair we extracted the LFP and spikes around each heartbeat. We then randomly mismatched these beat-locked LFP-traces with beat-locked spike trains. This shuffling procedure preserves beat-related changes in spikes and LFP but will disrupt any spike-LFP relationships that are not tied to the heart. We performed 200 bootstraps and recalculated the SFC and Kappa values. We then z-scored the SFC and Kappa data to these bootstrapped values to effectively subtract off any spurious cardiac-related spike-LFP relationships. For example, the neuron-LFP pair in Figure S9A has high spike-field coherence and Kappa values at low frequencies < 2 Hz due to the changes in firing rate and the LFP signal around the heartbeat due to electrode motion (Figure S9C). After z-scoring to shuffled data, this spurious coherence is removed without affecting underlying spike-field relationships (Figure S9D).
Statistical comparisons of spike and spike-LFP values were performed using nonparametric statistics, Kruskal-Wallis for multiple groups, Wilcoxon rank-sum for two groups (p < 0.05, corrected for multiple comparisons). Chi-square and Fishers-exact tests were used for comparisons of cell counts among groups and types of responses, e.g., comparing the number of BS1 and BS2 cells that synchronize to local theta.
Quantification of EAP waveform features
For each in vivo and model neuron we extracted from the high pass filtered 32 kHz signal, 32 samples (1 ms) before and 50 samples (1.56 ms) after the EAP extremum. We then upsampled this signal to 100 kHz and realigned all waveforms to the extremum.
We calculated four standard features of the average EAP waveform: extremum amplitude (AMP), half-width time (HW), trough-to-peak time (TPW), and repolarization time (REP) (Figure 1D). These EAP features are often used to delineate functional classes in vivo and in slice recordings (e.g., Anastassiou et al., 2015, Barthó et al., 2004, Ison et al., 2011, McCormick et al., 1985, Mitchell et al., 2007, Peyrache et al., 2012, Rutishauser et al., 2015, Trainito et al., 2019). AMP is the magnitude of the extremum of the EAP in microvolts. HW is the total time in milliseconds that the EAP trough dips below half the AMP value. TPW measures the time in milliseconds that elapses from the EAP trough to the EAP peak, the first local maximum after the trough. REP measures the amount of time required for the EAP to reach half of the peak value and is an estimate of the EAP repolarization time. In some brain regions, the EAP width features appeared to be bimodally distributed. To assess bimodality, we calculated the Hartigan’s Dip Test of multimodality. In addition, we assessed whether a single Gaussian distribution or a mixture of two Gaussian distributions better fit the distributions (assessed by minimizing Aikake Information Criterion for Gaussian mixture models with 1 or 2 distributions).
In addition to these features of the mean EAP waveform, we measured how these features change throughout the duration of the cardiac cycle. For in vivo data we binned the spikes in 100 ms bins that began 20 ms before each heartbeat ended at the median interbeat interval duration (804 ± 156 SD ms). We then averaged the EAP waveform of all the spikes that occurred in each bin to provide an average EAP waveform at each time during the cardiac cycle. We used these binned EAPs to calculate features at each time point in the cardiac cycle. For model data we calculated the average EAP at every location around the cell. We then selected a random location around the cell and sampled the average EAP sinusoidally from this fixed location to simulate cardiac motion (see model generation method).
For each average EAP during each cardiac bin, we calculated AMP, HW, TPW, and REP as above. Plotting these features against the phase of the cardiac cycle (as in Figure 1E) highlights how these features change as a function of cardiac motion. We divided each of these traces by their mean to give a percent change from mean. To quantify the strength of these changes we fit a cosine function to each trace using circular-linear regression. The amplitude of this cosine fit estimates the percent change in the feature during the cardiac cycle and is termed the Modulation Index (MI). For example, a value of 5 indicates that the feature increased up to 5% of its mean value throughout the duration of the cardiac cycle. AMP MI was said to be strongly modulated by the cardiac cycle if the amplitude of this sinusoidal fit was significantly different from zero (p < 0.05) and it was greater than 95% of bootstrap shuffled data. Bootstrapping was performed by shuffling the EAP waveforms associated with each spike time for 200 iterations.
In addition, we quantified the extent to which each width features covaried with AMP during the cardiac cycle using linear regression. We refer to the slope of this linear regression as the Motion Correlation (MC). A value of 0 indicates that the width feature did not vary with AMP. A value of −2 for TPW MC, for example indicates that TPW decreases by 2% for every 1% increase in AMP.
Identification of EAP waveform clusters using PCA and k-means clustering
To identify clusters of cell types in the experimental data, we performed principal component analysis on the normalized EAP features of the hippocampal neurons (Figure S2; Figures 2A and 2C). We only selected neurons with significant strongly modulated AMP MI for this analysis because we were interested in cells with EAP waveforms that were most affected by cardiac motion. We performed k-means clustering (k = 1-9 clusters, 1000 iterations with random starting locations) on the principal components that explained 90% of the variance of the EAP features (Figures S2A and S2B, 3 components in standard feature space, 7 components in standard + motion feature space). The optimal number of clusters was identified by minimizing the density function f(K) (Pham et al., 2005 as in Jia et al., 2019). f(K) is the ratio of the real distortion to the estimated distortion and has a value of 1 for uniformly distributed data. In the standard feature space (Figure 2A), f(k) is lowest for k = 2, indicating that 2 clusters is the optimal number of clusters. In addition to k-means clustering we performed hierarchical clustering with Ward linkage and present dendrograms (Figure 2E). Both approaches yield highly overlapping results. When only using standard features, we identified two cell classes, one with narrow spike (NS) and one with broad spike waveforms (BS). With the addition of motion features, BS cells clustered into two separate groups labeled BS1 and BS2. Clusters are shown with t-distributed stochastic neighbor embedding (tSNE) for visualization purposes only (van der Maaten and Hinton, 2008).
We used a similar PCA-kmeans approach to identify SP1 and SP2 model neuron types. First, we randomly selected 25 EAPs from different sites around each of the SP model neurons. We then applied PCA specifically to the motion features (MI and MC) of the SP waveforms and performed k-means clustering to identify 2 groups of EAPs: SP1 and SP2. These groups differed in multiple features, e.g., SP2 has more negative HW MC and TPW MC than SP1 (Figure 6B). We then tabulated the number of EAPs of each model that were assigned to either the SP1 or SP2 EAP cluster. A model neuron was labeled SP1 (or SP2) if the majority of its EAPs (> 13/25 EAPs) belonged to the SP1 (or SP2) cell cluster.
SVM Classification of EAPS
We trained several linear SVM classifiers to discriminate between different types of experimental EAPs (NS versus BS, BS1 versus BS2) and EAPs derived from model neurons (AP versus SP, SP1 versus SP2). For experimental-based classifiers, we trained and tested using random subsets of the experimentally-recorded EAPs and used the labels NS, BS1, and BS2 derived from the k-means clusters in Figure 2C. For the model-based classifiers, we randomly selected 25 EAPs with AMP 40 ± 20 microvolts (the distribution of EAP AMPs recorded in vivo). We then trained on the EAPs from a subset of models and tested on the EAPs from the remaining models. The model neurons were constructed from in vitro patch clamp recordings of human neurons and the AP and SP labels were determined by the morphological reconstructions of these neurons and their associated spines (see also section above on model generation). The SP1 and SP2 labels were derived from the EAP-feature k-means clustering described in the preceding section.
In all cases, each reported classifier is a “bootstrap composite” of 1,000 individual SVM classifiers each trained and tested on a different subset of EAPs to ensure robustness and generality to new data. The result of each composite classifier therefore gives both a classification label and a percent indicating the fraction of individual bootstrapped classifiers that assigned the same label. For example, the Standard Experiment-based Classifier (Figure 5A), assigned the neuron in Figure 1E middle panel the label BS with 99% agreement (i.e., 99% of the individual classifiers in this composite classifier gave the label BS). For each application of a classifier, labels were assigned based on more than 50% agreement of the individual classifiers, though most cells had much higher values (mean agreement = 96% ± 10% for the Standard Experiment-Based classifier in Figure 5A). Confusion matrices and accuracy bar-plots show the performance on left out data (e.g., Figure 5A). The SVM Beta coefficients estimate the contribution of each feature to the SVM plane that divides the classification space with higher values indicating a larger contribution to the classification model (e.g., Figure 5B).
The primary motivation for constructing classifiers was to cross-validate the experimental and model-based results. We applied experimental-based classifiers to model EAPs to identify model neurons in the experimental space (NS or BS, BS1 or BS2) (Figures 5C and 6F right). Similarly, we applied model-based classifiers to the experimental EAPs to identify experimental neurons in the model space (AP or SP, SP1 or SP2; Figures 5F and 6F left).
Data Code and Availability
Code for calculating EAP features and classifying cell types was custom-written in MATLAB and is available on GitHub (https://github.com/rutishauserlab/cellclassifier). The all-active human single-neuron models were constructed in Python and are also available on GitHub (https://github.com/AllenInstitute/Human_all_active_models_EAP).
Acknowledgments
We wish to thank the Allen Institute founder, Paul G. Allen, for his vision, encouragement, and support. We thank all members of the Anastassiou and Rutishauser labs for discussions, Shannon Sullivan, April Carlson, and Nand Chandravadia for their assistance in spike sorting, Anatoly Buchin and Tom Chartrand for their contributions to the optimization and simulation workflow, and Uygar Sümbül for critical comments and discussions. We gratefully acknowledge the willingness of our patients to participate in this study and the staff and physicians of the Epilepsy Monitoring Unit and the Movement Disorders Program at Cedars-Sinai Medical Center for their invaluable assistance. Research reported in this publication was supported by the National Institute of Mental Health, United States ( R01MH110831 to U.R.) and the National Institute of Neurological Disorders and Stroke, United States ( U01NS103792 , U01NS098961 to U.R.).
Author Contributions
C.P.M., J.K., A.N.M., and U.R. designed in vivo experiments and collected in vivo extracellular data. A.N., Y.W., and C.A.A. constructed the all-active human single-neuron models and simulated data. A.N.M. performed surgery and provided patient care. C.P.M. and Y.W. performed data analysis with guidance from C.A.A. and U.R. J.K. first noticed the cardiac-related changes in the electrophysiology. C.P.M. wrote the initial draft of the manuscript. All authors discussed the results at all stages of the project and contributed to the final manuscript.
Declaration of Interests
The authors declare no competing interests.
Supplemental Information
Download .pdf (1.62 MB)Help with pdf files
Document S1. Figures S1–S9 and Tables S1–S3
References
Aevermann B.D.
Novotny M.
Bakken T.
Miller J.A.
Diehl A.D.
Osumi-Sutherland D.
Lasken R.S.
Lein E.S.
Scheuermann R.H.
Cell type discovery using single-cell transcriptomics: implications for ontological representation.
Hum. Mol. Genet. 2018; 27: R40-R47
View in Article
Scopus (11)
PubMed
Crossref
Google Scholar
Allen J.J.B.
Chambers A.S.
Towers D.N.
The many metrics of cardiac chronotropy: a pragmatic primer and a brief comparison of metrics.
Biol. Psychol. 2007; 74: 243-262
View in Article
Scopus (279)
PubMed
Crossref
Google Scholar
Anastassiou C.A.
Shai A.S.
Psyche, signals and systems.
in: Buzsáki G. Christen Y. Micro-, Meso- and Macro-Dynamics of the Brain. Springer, 2016
View in Article
Scopus (2)
Crossref
Google Scholar
Anastassiou C.A.
Perin R.
Buzsáki G.
Markram H.
Koch C.
Cell type- and activity-dependent extracellular correlates of intracellular spiking.
J. Neurophysiol. 2015; 114: 608-623
View in Article
Scopus (27)
PubMed
Crossref
Google Scholar
Ardid S.
Vinck M.
Kaping D.
Marquez S.
Everling S.
Womelsdorf T.
Mapping of functionally characterized cell classes onto canonical circuit operations in primate prefrontal cortex.
J. Neurosci. 2015; 35: 2975-2991
View in Article
Scopus (28)
PubMed
Crossref
Google Scholar
Barthó P.
Hirase H.
Monconduit L.
Zugaro M.
Harris K.D.
Buzsáki G.
Characterization of neocortical principal cells and interneurons by network interactions and extracellular features.
J. Neurophysiol. 2004; 92: 600-608
View in Article
Scopus (410)
PubMed
Crossref
Google Scholar
Berens P.
CircStat: A MATLAB Toolbox for Circular Statistics.
J. Stat. Softw. 2009; 31: 1-21
View in Article
Crossref
Google Scholar
Buzsáki G.
Large-scale recording of neuronal ensembles.
Nat. Neurosci. 2004; 7: 446-451
View in Article
Scopus (1050)
PubMed
Crossref
Google Scholar
Buzsáki G.
Rhythms of the Brain.
Oxford University Press, 2006
View in Article
Scopus (2482)
Crossref
Google Scholar
Buzsáki G.
Draguhn A.
Neuronal oscillations in cortical networks.
Science. 2004; 304: 1926-1929
View in Article
Scopus (3119)
PubMed
Crossref
Google Scholar
Buzsáki G.
Penttonen M.
Nádasdy Z.
Bragin A.
Pattern and inhibition-dependent invasion of pyramidal cell dendrites by fast spikes in the hippocampus in vivo.
Proc. Natl. Acad. Sci. USA. 1996; 93: 9921-9925
View in Article
Scopus (185)
PubMed
Crossref
Google Scholar
Buzsáki G.
Anastassiou C.A.
Koch C.
The origin of extracellular fields and currents–EEG, ECoG, LFP and spikes.
Nat. Rev. Neurosci. 2012; 13: 407-420
View in Article
Scopus (1386)
PubMed
Crossref
Google Scholar
Carlson A.A.
Rutishauser U.
Mamelak A.N.
Safety and Utility of Hybrid Depth Electrodes for Seizure Localization and Single-Unit Neuronal Recording.
Stereotact. Funct. Neurosurg. 2018; 96: 311-319
View in Article
Scopus (3)
PubMed
Crossref
Google Scholar
Chen X.
Leischner U.
Varga Z.
Jia H.
Deca D.
Rochefort N.L.
Konnerth A.
LOTOS-based two-photon calcium imaging of dendritic spines in vivo.
Nat. Protoc. 2012; 7: 1818-1829
View in Article
Scopus (38)
PubMed
Crossref
Google Scholar
Connors B.W.
Gutnick M.J.
Intrinsic firing patterns of diverse neocortical neurons.
Trends Neurosci. 1990; 13: 99-104
View in Article
Scopus (989)
PubMed
Abstract
Full Text PDF
Google Scholar
DeFelipe J.
López-Cruz P.L.
Benavides-Piccione R.
Bielza C.
Larrañaga P.
Anderson S.
Burkhalter A.
Cauli B.
Fairén A.
Feldmeyer D.
et al.
New insights into the classification and nomenclature of cortical GABAergic interneurons.
Nat. Rev. Neurosci. 2013; 14: 202-216
View in Article
Scopus (382)
PubMed
Crossref
Google Scholar
Erondu N.E.
Kennedy M.B.
Regional distribution of type II Ca2+/calmodulin-dependent protein kinase in rat brain.
J. Neurosci. 1985; 5: 3270-3277
View in Article
PubMed
Crossref
Google Scholar
Eyal G.
Verhoog M.B.
Testa-Silva G.
Deitcher Y.
Lodder J.C.
Benavides-Piccione R.
Morales J.
DeFelipe J.
de Kock C.P.
Mansvelder H.D.
Segev I.
Unique membrane properties and enhanced signal processing in human neocortical neurons.
eLife. 2016; 5 (Published online October 6, 2016)
https://doi.org/10.7554/eLife.16553
View in Article
Scopus (43)
PubMed
Crossref
Google Scholar
Faraut M.C.M.
Carlson A.A.
Sullivan S.
Tudusciuc O.
Ross I.
Reed C.M.
Chung J.M.
Mamelak A.M.
Rutishauser U.
Dataset of human medial temporal lobe single neuron activity during declarative memory encoding and recognition.
Sci. Data. 2018; 5: 180010
https://doi.org/10.1038/sdata.2018.10
View in Article
Scopus (7)
PubMed
Crossref
Google Scholar
Fee M.S.
Active stabilization of electrodes for intracellular recording in awake behaving animals.
Neuron. 2000; 27: 461-468
View in Article
Scopus (62)
PubMed
Abstract
Full Text
Full Text PDF
Google Scholar
Fellous J.-M.
Houweling A.R.
Modi R.H.
Rao R.P.
Tiesinga P.H.
Sejnowski T.J.
Frequency dependence of spike timing reliability in cortical pyramidal cells and interneurons.
J. Neurophysiol. 2001; 85: 1782-1787
View in Article
PubMed
Crossref
Google Scholar
Freund T.F.
Buzsáki G.
Interneurons of the hippocampus.
Hippocampus. 1996; 6: 347-470
View in Article
PubMed
Crossref
Google Scholar
Fries P.
Reynolds J.H.
Rorie A.E.
Desimone R.
Modulation of oscillatory neuronal synchronization by selective visual attention.
Science. 2001; 291: 1560-1563
View in Article
Scopus (1767)
PubMed
Crossref
Google Scholar
Gold C.
Henze D.A.
Koch C.
Buzsáki G.
On the origin of the extracellular action potential waveform: A modeling study.
J. Neurophysiol. 2006; 95: 3113-3128
View in Article
Scopus (318)
PubMed
Crossref
Google Scholar
Gold C.
Henze D.A.
Koch C.
Using extracellular action potential recordings to constrain compartmental models.
J. Comput. Neurosci. 2007; 23: 39-58
View in Article
Scopus (84)
PubMed
Crossref
Google Scholar
González-Burgos G.
Miyamae T.
Krimer Y.
Gulchina Y.
Pafundo D.E.
Krimer O.
Bazmi H.
Arion D.
Enwright J.F.
Fish K.N.
Lewis D.A.
Distinct Properties of Layer 3 Pyramidal Neurons from Prefrontal and Parietal Areas of the Monkey Neocortex.
J. Neurosci. 2019; 39: 7277-7290
View in Article
Scopus (1)
PubMed
Crossref
Google Scholar
Gouwens N.W.
Sorensen S.A.
Berg J.
Lee C.
Jarsky T.
Ting J.
Sunkin S.M.
Feng D.
Anastassiou C.A.
Barkan E.
et al.
Classification of electrophysiological and morphological neuron types in the mouse visual cortex.
Nat. Neurosci. 2019; 22: 1182-1195
View in Article
Scopus (16)
PubMed
Crossref
Google Scholar
Gratiy S.L.
Billeh Y.N.
Dai K.
Mitelut C.
Feng D.
Gouwens N.W.
Cain N.
Koch C.
Anastassiou C.A.
Arkhipov A.
BioNet: A Python interface to NEURON for modeling large-scale networks.
PLoS ONE. 2018; 13: e0201630
View in Article
Scopus (14)
PubMed
Crossref
Google Scholar
Graves A.R.
Moore S.J.
Bloss E.B.
Mensh B.D.
Kath W.L.
Spruston N.
Hippocampal pyramidal neurons comprise two distinct cell types that are countermodulated by metabotropic receptors.
Neuron. 2012; 76: 776-789
View in Article
Scopus (90)
PubMed
Abstract
Full Text
Full Text PDF
Google Scholar
Gray C.M.
McCormick D.A.
Chattering cells: superficial pyramidal neurons contributing to the generation of synchronous oscillations in the visual cortex.
Science. 1996; 274: 109-113
View in Article
Scopus (594)
PubMed
Crossref
Google Scholar
Harris K.D.
Hochgerner H.
Skene N.G.
Magno L.
Katona L.
Bengtsson Gonzales C.
Somogyi P.
Kessaris N.
Linnarsson S.
Hjerling-Leffler J.
Classes and continua of hippocampal CA1 inhibitory neurons revealed by single-cell transcriptomics.
PLoS Biol. 2018; 16: e2006387
View in Article
Scopus (38)
PubMed
Crossref
Google Scholar
Hasenstaub A.
Shu Y.
Haider B.
Kraushaar U.
Duque A.
McCormick D.A.
Inhibitory postsynaptic potentials carry synchronized frequency information in active cortical networks.
Neuron. 2005; 47: 423-435
View in Article
Scopus (399)
PubMed
Abstract
Full Text
Full Text PDF
Google Scholar
Heck D.H.
McAfee S.S.
Liu Y.
Babajani-Feremi A.
Rezaie R.
Freeman W.J.
Wheless J.W.
Papanicolaou A.C.
Ruszinkó M.
Sokolov Y.
Kozma R.
Breathing as a Fundamental Rhythm of Brain Function.
Front. Neural Circuits. 2017; 10: 115
View in Article
Scopus (35)
PubMed
Crossref
Google Scholar
Hodge R.D.
Bakken T.E.
Miller J.A.
Smith K.A.
Barkan E.R.
Graybuck L.T.
Close J.L.
Long B.
Penn O.
Yao Z.
et al.
Conserved cell types with divergent features between human and mouse cortex (preprint).
Neuroscience. 2018; 573: 61-68
View in Article
Google Scholar
Holt G.R.
Koch C.
Electrical interactions via the extracellular potential near cell bodies.
J. Comput. Neurosci. 1999; 6: 169-184
View in Article
Scopus (205)
PubMed
Crossref
Google Scholar
Hunt D.L.
Linaro D.
Si B.
Romani S.
Spruston N.
A novel pyramidal cell type promotes sharp-wave synchronization in the hippocampus.
Nat. Neurosci. 2018; 21: 985-995
View in Article
Scopus (11)
PubMed
Crossref
Google Scholar
Hunt D.L.
Lai C.
Smith R.D.
Lee A.K.
Harris T.D.
Barbic M.
Multimodal in vivo brain electrophysiology with integrated glass microelectrodes.
Nat. Biomed. Eng. 2019; 3: 741-753
View in Article
Scopus (6)
PubMed
Crossref
Google Scholar
Isokawa-Akesson M.
Wilson C.L.
Babb T.L.
Diversity in periodic pattern of firing in human hippocampal neurons.
Exp. Neurol. 1987; 98: 137-151
View in Article
Scopus (14)
PubMed
Crossref
Google Scholar
Ison M.J.
Mormann F.
Cerf M.
Koch C.
Fried I.
Quiroga R.Q.
Selectivity of pyramidal cells and interneurons in the human medial temporal lobe.
J. Neurophysiol. 2011; 106: 1713-1721
View in Article
Scopus (36)
PubMed
Crossref
Google Scholar
Jia X.
Siegle J.H.
Bennett C.
Gale S.D.
Denman D.J.
Koch C.
Olsen S.R.
High-density extracellular probes reveal dendritic backpropagation and facilitate neuron classification.
J. Neurophysiol. 2019; 121: 1831-1847
View in Article
Scopus (1)
PubMed
Crossref
Google Scholar
Johnston K.
DeSouza J.F.X.
Everling S.
Monkey prefrontal cortical pyramidal and putative interneurons exhibit differential patterns of activity between prosaccade and antisaccade tasks.
J. Neurosci. 2009; 29: 5516-5524
View in Article
Scopus (46)
PubMed
Crossref
Google Scholar
Joshi S.
Hawken M.J.
Loose-patch-juxtacellular recording in vivo–a method for functional characterization and labeling of neurons in macaque V1.
J. Neurosci. Methods. 2006; 156: 37-49
View in Article
Scopus (40)
PubMed
Crossref
Google Scholar
Jun J.J.
Mitelut C.
Lai C.
Gratiy S.L.
Anastassiou C.A.
Harris T.D.
Real-time spike sorting platform for high-density extracellular probes with ground-truth validation and drift correction.
bioRxiv. 2017;
https://doi.org/10.1101/101030
View in Article
Crossref
Google Scholar
Kamiński J.
Sullivan S.
Chung J.M.
Ross I.B.
Mamelak A.N.
Rutishauser U.
Persistently active neurons in human medial frontal and medial temporal lobe support working memory.
Nat. Neurosci. 2017; 20: 590-601
View in Article
Scopus (45)
PubMed
Crossref
Google Scholar
Kamiński J.
Mamelak A.N.
Birch K.
Mosher C.P.
Tagliati M.
Rutishauser U.
Novelty-Sensitive Dopaminergic Neurons in the Human Substantia Nigra Predict Success of Declarative Memory Formation.
Curr. Biol. 2018; 28: 1333-1343
View in Article
Scopus (11)
PubMed
Abstract
Full Text
Full Text PDF
Google Scholar
Kern M.
Aertsen A.
Schulze-Bonhage A.
Ball T.
Heart cycle-related effects on event-related potentials, spectral power changes, and connectivity patterns in the human ECoG.
Neuroimage. 2013; 81: 178-190
View in Article
Scopus (43)
PubMed
Crossref
Google Scholar
Kim K.
Ladenbauer J.
Babo-Rebelo M.
Buot A.
Lehongre K.
Adam C.
Hasboun D.
Lambrecq V.
Navarro V.
Ostojic S.
Tallon-Baudry C.
Resting-State Neural Firing Rate Is Linked to Cardiac-Cycle Duration in the Human Cingulate and Parahippocampal Cortices.
J. Neurosci. 2019; 39: 3676-3686
View in Article
Scopus (4)
PubMed
Crossref
Google Scholar
Klausberger T.
Somogyi P.
Neuronal diversity and temporal dynamics: the unity of hippocampal circuit operations.
Science. 2008; 321: 53-57
View in Article
Scopus (1141)
PubMed
Crossref
Google Scholar
Klausberger T.
Magill P.J.
Márton L.F.
Roberts J.D.B.
Cobden P.M.
Buzsáki G.
Somogyi P.
Brain-state- and cell-type-specific firing of hippocampal interneurons in vivo.
Nature. 2003; 421: 844-848
https://doi.org/10.1038/nature01374
View in Article
Scopus (879)
PubMed
Crossref
Google Scholar
Koch C.
Biophysics of Computation: Information Processing in Single Neurons.
Oxford University Press, 2004
View in Article
Google Scholar
Kohara K.
Pignatelli M.
Rivest A.J.
Jung H.-Y.
Kitamura T.
Suh J.
Frank D.
Kajikawa K.
Mise N.
Obata Y.
et al.
Cell type-specific genetic and optogenetic tools reveal hippocampal CA2 circuits.
Nat. Neurosci. 2014; 17: 269-279
View in Article
Scopus (202)
PubMed
Crossref
Google Scholar
Krimer L.S.
Zaitsev A.V.
Czanner G.
Kröner S.
González-Burgos G.
Povysheva N.V.
Iyengar S.
Barrionuevo G.
Lewis D.A.
Cluster analysis-based physiological classification and morphological properties of inhibitory neurons in layers 2-3 of monkey dorsolateral prefrontal cortex.
J. Neurophysiol. 2005; 94: 3009-3022
View in Article
Scopus (90)
PubMed
Crossref
Google Scholar
Logothetis N.K.
Kayser C.
Oeltermann A.
In vivo measurement of cortical impedance spectrum in monkeys: implications for signal propagation.
Neuron. 2007; 55: 809-823
View in Article
Scopus (263)
PubMed
Abstract
Full Text
Full Text PDF
Google Scholar
Markram H.
Toledo-Rodriguez M.
Wang Y.
Gupta A.
Silberberg G.
Wu C.
Interneurons of the neocortical inhibitory system.
Nat. Rev. Neurosci. 2004; 5: 793-807
View in Article
Scopus (1767)
PubMed
Crossref
Google Scholar
McCormick D.A.
Connors B.W.
Lighthall J.W.
Prince D.A.
Comparative electrophysiology of pyramidal and sparsely spiny stellate neurons of the neocortex.
J. Neurophysiol. 1985; 54: 782-806
View in Article
Scopus (1356)
PubMed
Crossref
Google Scholar
Mendoza G.
Peyrache A.
Gámez J.
Prado L.
Buzsáki G.
Merchant H.
Recording extracellular neural activity in the behaving monkey using a semichronic and high-density electrode system.
J. Neurophysiol. 2016; 116: 563-574
View in Article
Scopus (10)
PubMed
Crossref
Google Scholar
Millhouse O.E.
DeOlmos J.
Neuronal configurations in lateral and basolateral amygdala.
Neuroscience. 1983; 10: 1269-1300
View in Article
Scopus (126)
PubMed
Crossref
Google Scholar
Mitchell J.F.
Sundberg K.A.
Reynolds J.H.
Differential attention-dependent response modulation across cell classes in macaque visual area V4.
Neuron. 2007; 55: 131-141
View in Article
Scopus (392)
PubMed
Abstract
Full Text
Full Text PDF
Google Scholar
Nelson M.J.
Pouget P.
Physical model of coherent potentials measured with different electrode recording site sizes.
J. Neurophysiol. 2012; 107: 1291-1300
View in Article
Scopus (7)
PubMed
Crossref
Google Scholar
Oemisch M.
Westendorff S.
Everling S.
Womelsdorf T.
Interareal Spike-Train Correlations of Anterior Cingulate and Dorsal Prefrontal Cortex during Attention Shifts.
J. Neurosci. 2015; 35: 13076-13089
View in Article
Scopus (20)
PubMed
Crossref
Google Scholar
Onorato I.
Neuenschwander S.
Hoy J.
Lima B.
Rocha K.-S.
Broggini A.C.
Uran C.
Spyropoulos G.
Klon-Lipok J.
Womelsdorf T.
et al.
A Distinct Class of Bursting Neurons with Strong Gamma Synchronization and Stimulus Selectivity in Monkey V1.
Neuron. bioRxiv. 2020;
https://doi.org/10.1016/j.neuron.2019.09.039
View in Article
Scopus (1)
Abstract
Full Text
Full Text PDF
Google Scholar
Pedemonte M.
Goldstein-Daruech N.
Velluti R.A.
Temporal correlations between heart rate, medullary units and hippocampal theta rhythm in anesthetized, sleeping and awake guinea pigs.
Auton. Neurosci. 2003; 107: 99-104
View in Article
Scopus (19)
PubMed
Abstract
Full Text
Full Text PDF
Google Scholar
Pettersen K.H.
Einevoll G.T.
Amplitude variability and extracellular low-pass filtering of neuronal spikes.
Biophys. J. 2008; 94: 784-802
View in Article
Scopus (132)
PubMed
Abstract
Full Text
Full Text PDF
Google Scholar
Peyrache A.
Destexhe A.
Electrophysiological monitoring of inhibition in mammalian species, from rodents to humans.
Neurobiol. Dis. 2019; 130: 104500
View in Article
Scopus (1)
PubMed
Crossref
Google Scholar
Peyrache A.
Dehghani N.
Eskandar E.N.
Madsen J.R.
Anderson W.S.
Donoghue J.A.
Hochberg L.R.
Halgren E.
Cash S.S.
Destexhe A.
Spatiotemporal dynamics of neocortical excitation and inhibition during human sleep.
Proc. Natl. Acad. Sci. USA. 2012; 109: 1731-1736
View in Article
Scopus (77)
PubMed
Crossref
Google Scholar
Pham D.T.
Dimov S.S.
Nguyen C.D.
Selection of K in K-means clustering.
(Published online January 1, 2005)
https://journals.sagepub.com/doi/abs/10.1243/095440605X8298?cookieSet=1
Date: 2005
View in Article
Google Scholar
Rao S.G.
Williams G.V.
Goldman-Rakic P.S.
Isodirectional tuning of adjacent interneurons and pyramidal cells during working memory: evidence for microcolumnar organization in PFC.
J. Neurophysiol. 1999; 81: 1903-1916
View in Article
Scopus (238)
PubMed
Crossref
Google Scholar
Rutishauser U.
Schuman E.M.
Mamelak A.N.
Online detection and sorting of extracellularly recorded action potentials in human medial temporal lobe recordings, in vivo.
J. Neurosci. Methods. 2006; 154: 204-224
View in Article
Scopus (172)
PubMed
Crossref
Google Scholar
Rutishauser U.
Schuman E.M.
Mamelak A.N.
Activity of human hippocampal and amygdala neurons during retrieval of declarative memories.
Proc. Natl. Acad. Sci. USA. 2008; 105: 329-334
View in Article
Scopus (65)
PubMed
Crossref
Google Scholar
Rutishauser U.
Ross I.B.
Mamelak A.N.
Schuman E.M.
Human memory strength is predicted by theta-frequency phase-locking of single neurons.
Nature. 2010; 464: 903-907
View in Article
Scopus (335)
PubMed
Crossref
Google Scholar
Rutishauser U.
Ye S.
Koroma M.
Tudusciuc O.
Ross I.B.
Chung J.M.
Mamelak A.N.
Representation of retrieval confidence by single neurons in the human medial temporal lobe.
Nat. Neurosci. 2015; 18: 1041-1050
View in Article
Scopus (48)
PubMed
Crossref
Google Scholar
Schomburg E.W.
Anastassiou C.A.
Buzsáki G.
Koch C.
The spiking component of oscillatory extracellular potentials in the rat hippocampus.
J. Neurosci. 2012; 32: 11798-11811
View in Article
Scopus (102)
PubMed
Crossref
Google Scholar
Senzai Y.
Buzsáki G.
Physiological Properties and Behavioral Correlates of Hippocampal Granule Cells and Mossy Cells.
Neuron. 2017; 93: 691-704
View in Article
Scopus (64)
PubMed
Abstract
Full Text
Full Text PDF
Google Scholar
Shinomoto S.
Shima K.
Tanji J.
Differences in spiking patterns among cortical neurons.
Neural Comput. 2003; 15: 2823-2842
View in Article
Scopus (111)
PubMed
Crossref
Google Scholar
Sirota A.
Montgomery S.
Fujisawa S.
Isomura Y.
Zugaro M.
Buzsáki G.
Entrainment of neocortical neurons and gamma oscillations by the hippocampal theta rhythm.
Neuron. 2008; 60: 683-697
View in Article
Scopus (525)
PubMed
Abstract
Full Text
Full Text PDF
Google Scholar
Soltesz I.
Losonczy A.
CA1 pyramidal cell diversity enabling parallel information processing in the hippocampus.
Nat. Neurosci. 2018; 21: 484-493
View in Article
Scopus (35)
PubMed
Crossref
Google Scholar
Spampanato J.
Polepalli J.
Sah P.
Interneurons in the basolateral amygdala.
Neuropharmacology. 2011; 60: 765-773
View in Article
Scopus (97)
PubMed
Crossref
Google Scholar
Spruston N.
Pyramidal neurons: dendritic structure and synaptic integration.
Nat. Rev. Neurosci. 2008; 9: 206-221
View in Article
Scopus (825)
PubMed
Crossref
Google Scholar
Srivastava G.
Crottaz-Herbette S.
Lau K.M.
Glover G.H.
Menon V.
ICA-based procedures for removing ballistocardiogram artifacts from EEG data acquired in the MRI scanner.
Neuroimage. 2005; 24: 50-60
View in Article
Scopus (204)
PubMed
Crossref
Google Scholar
Staba R.J.
Wilson C.L.
Fried I.
Engel Jr., J.
Single neuron burst firing in the human hippocampus during sleep.
Hippocampus. 2002; 12: 724-734
View in Article
Scopus (38)
PubMed
Crossref
Google Scholar
Stauffer W.R.
Lak A.
Yang A.
Borel M.
Paulsen O.
Boyden E.S.
Schultz W.
Dopamine Neuron-Specific Optogenetic Stimulation in Rhesus Macaques.
Cell. 2016; 166: 1564-1571
View in Article
Scopus (76)
PubMed
Abstract
Full Text
Full Text PDF
Google Scholar
Takahashi K.
Kim S.
Coleman T.P.
Brown K.A.
Suminski A.J.
Best M.D.
Hatsopoulos N.G.
Large-scale spatiotemporal spike patterning consistent with wave propagation in motor cortex.
Nat. Commun. 2015; 6: 7169
View in Article
Scopus (31)
PubMed
Crossref
Google Scholar
Tamura H.
Kaneko H.
Kawasaki K.
Fujita I.
Presumed inhibitory neurons in the macaque inferior temporal cortex: visual response properties and functional interactions with adjacent neurons.
J. Neurophysiol. 2004; 91: 2782-2796
View in Article
Scopus (47)
PubMed
Crossref
Google Scholar
Tasic B.
Yao Z.
Graybuck L.T.
Smith K.A.
Nguyen T.N.
Bertagnolli D.
Goldy J.
Garren E.
Economo M.N.
Viswanathan S.
et al.
Shared and distinct transcriptomic cell types across neocortical areas.
Nature. 2018; 563: 72-78
View in Article
Scopus (115)
PubMed
Crossref
Google Scholar
Taxidis J.
Anastassiou C.A.
Diba K.
Koch C.
Local Field Potentials Encode Place Cell Ensemble Activation during Hippocampal Sharp Wave Ripples.
Neuron. 2015; 87: 590-604
View in Article
Scopus (22)
PubMed
Abstract
Full Text
Full Text PDF
Google Scholar
Terem I.
Ni W.W.
Goubran M.
Rahimi M.S.
Zaharchuk G.
Yeom K.W.
Moseley M.E.
Kurt M.
Holdsworth S.J.
Revealing sub-voxel motions of brain tissue using phase-based amplified MRI (aMRI).
Magn. Reson. Med. 2018; 80: 2549-2559
View in Article
Scopus (10)
PubMed
Crossref
Google Scholar
Tort A.B.L.
Brankačk J.
Draguhn A.
Respiration-Entrained Brain Rhythms Are Global but Often Overlooked.
Trends Neurosci. 2018; 41: 186-197
View in Article
Scopus (39)
PubMed
Abstract
Full Text
Full Text PDF
Google Scholar
Trainito C.
von Nicolai C.
Miller E.K.
Siegel M.
Extracellular Spike Waveform Dissociates Four Functionally Distinct Cell Classes in Primate Cortex.
Curr. Biol. 2019; 29: 2973-2982.e5
View in Article
Scopus (3)
PubMed
Abstract
Full Text
Full Text PDF
Google Scholar
van der Maaten L.
Hinton G.
Visualizing Data using t-SNE.
J. Mach. Learn. Res. 2008; 9: 2579-2605
View in Article
Google Scholar
Van Geit W.
Gevaert M.
Chindemi G.
Rössert C.
Courcol J.-D.
Muller E.B.
Schürmann F.
Segev I.
Markram H.
BluePyOpt: Leveraging Open Source Software and Cloud Infrastructure to Optimise Model Parameters in Neuroscience.
Front. Neuroinform. 2016; 10: 17
View in Article
Scopus (32)
PubMed
Crossref
Google Scholar
Vigneswaran G.
Kraskov A.
Lemon R.N.
Large identified pyramidal cells in macaque motor and premotor cortex exhibit “thin spikes”: implications for cell type classification.
J. Neurosci. 2011; 31: 14235-14242
View in Article
Scopus (89)
PubMed
Crossref
Google Scholar
Viskontas I.V.
Ekstrom A.D.
Wilson C.L.
Fried I.
Characterizing interneuron and pyramidal cells in the human medial temporal lobe in vivo using extracellular recordings.
Hippocampus. 2007; 17: 49-57
View in Article
Scopus (41)
PubMed
Crossref
Google Scholar
Washburn M.S.
Moises H.C.
Electrophysiological and morphological properties of rat basolateral amygdaloid neurons in vitro.
J. Neurosci. 1992; 12: 4066-4079
View in Article
PubMed
Crossref
Google Scholar
Wilson F.A.W.
Functional synergism between putative y-aminobutyrate-containing neurons and pyramidal neurons in prefrontal cortex.
Proc. Natl. Acad. Sci. USA. 1994; 91: 4009-4013
View in Article
Scopus (229)
PubMed
Crossref
Google Scholar
Yelnik J.
Percheron G.
Subthalamic neurons in primates: a quantitative and comparative analysis.
Neuroscience. 1979; 4: 1717-1743
View in Article
Scopus (106)
PubMed
Crossref
Google Scholar
Zanos S.
Zanos T.P.
Marmarelis V.Z.
Ojemann G.A.
Fetz E.E.
Relationships between spike-free local field potentials and spike timing in human temporal cortex.
J. Neurophysiol. 2012; 107: 1808-1821
View in Article
Scopus (27)
PubMed
Crossref
Google Scholar
Zelano C.
Jiang H.
Zhou G.
Arora N.
Schuele S.
Rosenow J.
Gottfried J.A.
Nasal Respiration Entrains Human Limbic Oscillations and Modulates Cognitive Function.
J. Neurosci. 2016; 36: 12448-12467
View in Article
Scopus (66)
PubMed
Crossref
Google Scholar
Article Info
Publication History
Published: March 10, 2020
Accepted: February 5, 2020
Received in revised form: December 23, 2019
Received: September 9, 2019
Identification
DOI: https://doi.org/10.1016/j.celrep.2020.02.027

Copyright
© 2020 The Author(s).
User License
Creative Commons Attribution – NonCommercial – NoDerivs (CC BY-NC-ND 4.0) | How you can reuse Information Icon
ScienceDirect
Access this article on ScienceDirect
Figures
Figure thumbnail fx1
Graphical Abstract
Figure thumbnail gr1
Figure 1Extracellular Action Potential Waveforms in the Human Brain Are Modulated by the Cardiac Cycle
Figure thumbnail gr2
Figure 2Motion Features Identify Three EAP Clusters in Human HIPP (NS, BS1, and BS2)
Figure thumbnail gr3
Figure 3Optimization Workflow for Single-Cell All-Active Models of Human Cortical Neurons
Figure thumbnail gr4
Figure 4Simulated Electrode Motion in All-Active, Biophysically Realistic Models of Human Neurons
Figure thumbnail gr5
Figure 5In Vivo NS and BS Units Map onto Single-Cell SP and AP Models
Figure thumbnail gr6
Figure 6Two Types of Hippocampal Broad-Spike Waveform Cells (BS1 and BS2) Are Identified In Vivo
Figure thumbnail gr7
Figure 7NS, BS1, and BS2 Cells in the Human HIPP Exhibit Distinct Spike Patterns and Phase Coupling Properties In Vivo
Related Articles
The Extracellular RNA Communication Consortium: Establishing Foundational Knowledge and Technologies for Extracellular RNA Research
Das et al.
CellApril 04, 2019
In BriefFull-TextPDF
Open Archive
exRNA Atlas Analysis Reveals Distinct Extracellular RNA Cargo Types and Their Carriers Present across Human Biofluids
Murillo et al.
CellApril 04, 2019
In BriefFull-TextPDF
Open Archive
Mapping Extracellular RNA Sheds Lights on Distinct Carriers
Lässer
CellApril 04, 2019
In BriefFull-TextPDF
Open Archive
The Extracellular Surface of the GLP-1 Receptor Is a Molecular Trigger for Biased Agonism
Wootten et al.
CellJune 16, 2016
In BriefFull-TextPDF
Open Access
The Utilization of Extracellular Proteins as Nutrients Is Suppressed by mTORC1
Palm et al.
CellJuly 16, 2015
In BriefFull-TextPDF
Open Archive