POJ（8463）-----Stupid cat & Doge（openjudge）

Stupid cat & Doge

描述
动物园的规划和城市规划一样是个令人头疼的大问题。不幸的是，动物园规划师R.V.L.先生高估了小动物们的智商，他设计了一个极其复杂的动物园道路规划方案，如下图所示：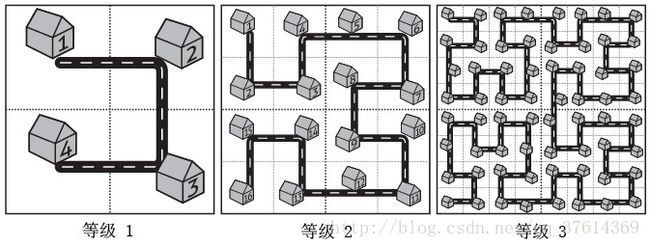
动物园按照下述方法进行扩建：当动物园规模扩大之后，R.V.L.先生设计的解决方案是把与原来动物园结构一样的区域复制或旋转90度之后按照图中的方式建设在原来的动物园周围（即将原来的动物园复制一遍放在原动物园上方，将顺时针旋转90度后的动物园放在原动物园的左上方，将逆时针旋转90度后的动物园放在原动物园的左方），再用道路将四部分的首尾连接起来，即可提升动物园的等级。

容易看出，等级提升后的动物园仍然是由一条道路连接，等级为N的动物园共能容纳2^2N只小动物，每只小动物将被分配到唯一的一间房屋。对于任意等级的动物园，我们从左上角开始沿着唯一的道路走，按照道路为房屋标号，就能够得到每间房屋的编号了。

说了这么多，智商余额不足的Stupid cat和Doge早已晕头转向。他们想知道，如果城市发展到了一定等级，他俩各自所处的房屋之间的直线距离是多少。房屋之间的距离是指两座房屋中心点之间的距离，你可以认为每间房屋都是边长为10米的正方形。

输入
输入包含多组测试数据，第一行有一个整数 T 表示测试数据的数目。
每组测试数据包含一行用空格隔开的三个整数 N, S, D，表示动物园等级，Stupid cat分配到的房屋编号和Doge分配到的房间编号。

输出
对于每组测试数据，在单独的一行内输出答案，四舍五入到整数。

样例输入

3
1 1 2
2 16 1
3 4 33

样例输出

10
30
50

【数据范围】
N≤31，1≤S,D≤2^2N，1≤T≤10000.

此题收录在NOI-openjudge中
做题地址：NOI-openjudge(需要注册)
2.4板块（分治）第8463题

---

作者血泪史

# 结果 时间
16 Accepted 05-20
15 Wrong Answer 05-20
14 Wrong Answer 05-20
13 Wrong Answer 05-20
12 Wrong Answer 05-20
11 Runtime Error 05-17
10 Wrong Answer 05-17
9 Wrong Answer 05-13
8 Wrong Answer 05-10
7 Runtime Error 05-10
6 Wrong Answer 05-09
5 Runtime Error 05-09
4 Runtime Error 05-09
3 Runtime Error 05-09
2 Compile Error 05-05
1 Runtime Error 05-05

究其根本原因，此题太水（假的假的都是假的）

---

分析题目可得

此题类型为分治+递归
变量需用long long int
递归需要分层次
分成4个板块（区域），每个板块对应一种变换
需要求坐标（算距离）

---

做题步骤分析

---

一：基本变量
1：坐标（求距离）
2：输入数据（编号）
3：……

二：程序基本框架

int main（）(主程序框架)

1：读测试数据（组数）
2：for循环读每组数据
3：函数递归
4：算距离（勾股定理）
5：输出
6：return

void f（）(递归+分治函数框架)

1：判断边界
2：查找上一等级区域
3：递归
4：分治求坐标
5：return

---

附代码一份（可先跳过）

#include
#include
#include
#include
#include
#include
//using namespace std;  使用会导致编译失败因为
void f(int n,long long m,long long &x,long long &y)
{
    if(n==0)    //边界
        return ;
    long long k=pow(2,n-1),l;
    for(l=0;l<4;l++)
        if((l+1)*k*k>=m)break;  //查找递归上一等级的区域
    f(n-1,m-(l*k*k),x,y);   //递归
    long long ax=x,ay=y;    //提前定义会错误
    switch(l)
    {
        case 0:x=ay;y=ax;break;
        case 1:y+=k;break;  
        case 2:x+=k;y+=k;break;
        case 3:x=ay;y=ax;x=k-x-1;y=k-y-1;x+=k;break;
    }
    return ;
}
int main()
{
    long long x1,y1,x2,y2,s,d;
    int L,N;
    scanf("%d",&L);
    for(int i=1;i<=L;i++)
    {
        scanf("%d %lld %lld",&N,&s,&d);
        x1=y1=x2=y2=0;
        f(N,s,x1,y1);
        f(N,d,x2,y2);
        long long ii=round(sqrt(pow((x1-x2)*10,2)+pow((y1-y2)*10,2)));
        printf("%lld\n",ii);
    }
}

---

IN THE END

如果你跳过了代码，由于此题太水，你可以先自己思考实践，在跟上方代码对拍，看看自己差了哪些。
这道题的递归体现在向上一个等级回退查找，而分治体现在对每一个区域的划分与处理。