FFT应用于多项式乘法

前言：花了一个上午，翻阅了算法导论和数篇博客来阅读这一块儿的知识，总算是弄明白了一个大概。学习就是一个自我总结的过程，知识呀，它不能只进不出。所以想自己写一篇博客来记录我这一上午的学习成果，尽量用最通俗易懂的语言和方法，对这一块的内容做一个自我论述。私以为既然都是IT民工，一些数学方面的基础知识我就不在博客里面提及了。但请一定要仔细阅读，我尽我所能将关键的地方阐述的清楚点。话不多说，下面就让我们进入正题吧。

FFT

首先要说明一下什么是FFT以及FFT主要用于什么。

快速傅里叶变换 (fast Fourier transform)，即利用计算机计算离散傅里叶变换（DFT)的高效、快速计算方法的统称，简称FFT。它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。它对傅氏变换的理论并没有新的发现，但是对于在计算机系统或者说数字系统中应用离散傅立叶变换，可以说是进了一大步。傅里叶变换最常见的用途是信号处理，这同样是快速傅里叶变换的常见用途。日常应用主要见于压缩技术、编码数字视频和音频信息。

不用管这上面说的是啥，你只要知道，多项式相加的最直接方法所需的时间为$O(n)$，但是相乘的最直接方法所需的时间达到了$O(n^2)$。而FFT的可以使多项式相乘的时间复杂度降为$O(n\lg n)$。

多项式的性质

在进一步了解FFT的具体实现过程之前，我们需要知道一些扩展的基础知识。

多项式的表达方法

系数表示：
一个以x为变量的n次多项式可以用如下形式表示：
$$A(x)=\sum _{j=0}^{n-1}{a}_j{x}^j=a_0+a_1{x}^1+a_2{x}^2+a_3{x}^3+...+a_{n-1}{x}^{n-1}$$我们称$a_0,a_1,...,a_{n-1}$为如上多项式的系数。如果A(x)的最高次项的系数是k，则称A(x)的次数是k，即为degree(A) = k。任何大于k的整数都是该多项式的次数界，比如k + 1、k + 2等都能称为$A(x)$的次数界。反过来，对于次数界为k的多项式，其次数可以是0~n - 1之间的任何整数，包括0和n - 1。好了，关于系数表示法知道这些就好了，小概念了解一下就行，重点是知晓其表示方法。
点值表示：
我们看着系数表示中$A(x)$的表达式，如果我们将n个不同的点$x_0,x_1,...,x_{n-1}$分别代入$A(x)$，那么我们就能得到n个不同的值$y_0,y_1,...,y_{n-1}$。我们就称由这n个点值对所组成的集合为点值表示：
$$\{(x_0,y_0),(x_1,y_1),...,(x_{n-1},y_{n-1})\}$$或者：$$\{(x_0,A(x_0)),(x_1,A(x_1)),...,(x_{n-1},A(x_{n-1})\}$$不能理解的话，看看其矩阵形式：$$\left[\begin{array}{c}A(x_0)\\ A(x_1)\\ A(x_2)\\ ...\\ A(x_{n-1})\end{array}\right]=\left[\begin{array}{ccccc}1& x_0& x_0^2& ...& x_0^{n-1}\\ 1& x_1& x_1^2& ...& x_1^{n-1}\\ 1& x_2& x_2^2& ...& x_2^{n-1}\\ ...& ...& ...& ...& ...\\ 1& x_{n-1}& x_{n-1}^2& ...& x_{n-1}^{n-1}\end{array}\right]\left[\begin{array}{c}{a}_0\\ a_1\\ a_2\\ ...\\ a_{n-1}\end{array}\right]$$相信此时此刻的你一定还在一头雾水，说这些有什么用呢？别急，这都是帮助你了解FFT和DFT的必要过程，牢记于心。

多项式的乘法形式

我们知道，对于两个多项式$A(x)$和$B(x)$来说，其直接乘法的时间是$O(n^2)$，而且：
$$C(x)=A(x)\times B(x)$$我们来看看点值表示的多项式的乘法。因为：
$$A(x)=\{(x_0,A(x_0)),(x_1,A(x_1)),...,(x_{n-1},A(x_{n-1}))\}$$$$B(x)=\{(x_0,B(x_0)),(x_1,B(x_1)),...,(x_{n-1},B(x_{n-1}))\}$$于是$C(x)$同样能用点值表示：
$$C(x)=\{(x_0,C(x_0)),(x_1,C(x_1),...,(x_{n-1},C(x_{n-1}))\}$$其中$C(x_k)=A(x_k)\times B(x_k),k=0,1,2,...,n-1。$
易知，点值表示的两个多项式相乘，只需要$O(n)$的时间，所以我们很自然地想到，能否够利用基于点值表达的多项式的线性时间乘法算法，来加速基于系数表达的多项式乘法运算呢？

多项式乘法的实现

要想用点值表示计算多项式乘法，关键点在于如何把系数表示转为点值表示以及逆运算把系数表示转点值表示。通常而言，我们把系数表示转点值表示称为“求值”，把点值表示转系数表示称为“插值”。
给定一个FFT，我们有下面时间复杂度为$O(n\lg n)$的方法，该方法把两个次数界为n的多项式$A(x)$和$B(x)$进行乘法运算，其中输入与输出均采用系数表示。这里有一个点要注意，两个次数界为n的多项式乘积是一个次数界为2n的多项式。

1. 加倍次数界：通过加入n个系数为0的高阶系数，把多项式$A(x)$和$B(x)$变为次数皆为2n的多项式，并构造其系数表示。
2. 求值：通过应用2n阶的FFT计算出$A(x)$和$B(x)$的长度为2n的点值表示。这些点值表示包含了两个多项式在2n次单位根处的取值。
3. 逐点相乘：把$A(x)$和$B(x)$的值逐个相乘，可以计算出多项式$C(x)=A(x)\times B(x)$的点值表示，这个表示中包含了$C(x)$在每个2n次单位根处的值。
4. 插值：通过对2n个点值对应用FFT，计算其逆DFT，就可以构造出多项式$C(x)$的系数表示。

上面这四个步骤看不懂不要紧，你只要知道大概的过程就是：系数表示转点值表示–>计算乘积–>点值表示转系数表示。

DFT与FFT

首先我们理清这两者的关系：

DFT(离散傅里叶变换)就是系数表示转点值表示的结果，IDFT(反离散傅里叶变换)就是系数表示转点值表示的结果。而我们把所有能够加快求解DFT过程的算法称为FFT，相对于的加快IDFT的称为IFFT。
暂时不用太过于纠结DFT的具体含义，只需要知道向量$y=(y_0,y_1,...,y_{n-1})$，就是系数向量$a=(a_0,a_1,...,a_{n-1})$的离散傅里叶变换。

暴力求解系数转点值和点值转系数仍然是一个时间为$O(n^2)$的方法，因此我们希望寻求能够降低$O(n^2)$的优化策略。
点值的表示中的x是可以任意的，这意味着实数和复数都能代入进行运算。我们希望找到一些特殊的值，使得$x^j=x^k,j,k=0,1,2,...,n-1$。比如1、-1、$i^2$这类比较特殊的值。在这里我们引入单位复数根的概念。

复数知识扩展

在引入单位复数根这个概念之前，先补充点关于复数的知识，过于基础的部分我就不赘述了：

复数的运算
加法：$(a+bi)+(c+di)=(a+c)+(b+d)i$
减法：$(a+bi)-(c+di)=(a-c)+(b-d)i$
乘法：$(a+bi)\ast (c+di)=(ac-bd)+(ad+bc)i$
类似于实数的性质，复数可以像向量一样在复平面中绘制，同样复数也可以像实数一样用极坐标来表示。
极坐标下复数相乘的规则：模长相乘，幅角相加：
$$(r_1,{\theta }_1)\ast (r_2,{\theta }_2)=(r_1\ast r_2,{\theta }_1+{\theta }_2)$$C++引入complex头文件后，只需用cpmplex x;即可定义一个复数。

这是一个非常有用的性质：如果两个复数的模为1，那么他们的乘积也为1，只不过是幅角增大了而已。我们要寻求n个模为1的数，自然就能想到单位圆。

单位复数根

n次单位复数根是满足${\omega }^n=1$的复数$\omega$。显然该方程有n个解，说明n次单位复数根恰好有n个，这些根的表达式是
$${\omega }_n=cos(\frac{2\pi }{n})+isin(\frac{2\pi }{n})$$则n次单位复数根就是${\omega }_0,{\omega }_1,...,{\omega }_{n-1}$通项公式为：
$${\omega }_n^k=cos(\frac{2\pi k}{n})+isin(\frac{2\pi k}{n})$$其中$k=0,1,...,n-1$。下图说明n个单位复数根均匀地分布在以复平面原点为圆心的单位圆上，值$${\omega }_n=e^{2\pi i/n}$$称为主n次单位根，如${\omega }_8=e^{2\pi i/8}$是主8次单位根。所有其他n次单位复数根都是${\omega }_n$的幂次，${\omega }_n^k$就是${\omega }_n^1$的$k$次方，如${\omega }_8^4=({\omega }_8^0{)}^4=1$。就当正常的数来看待就行，不要认为是很复杂的概念。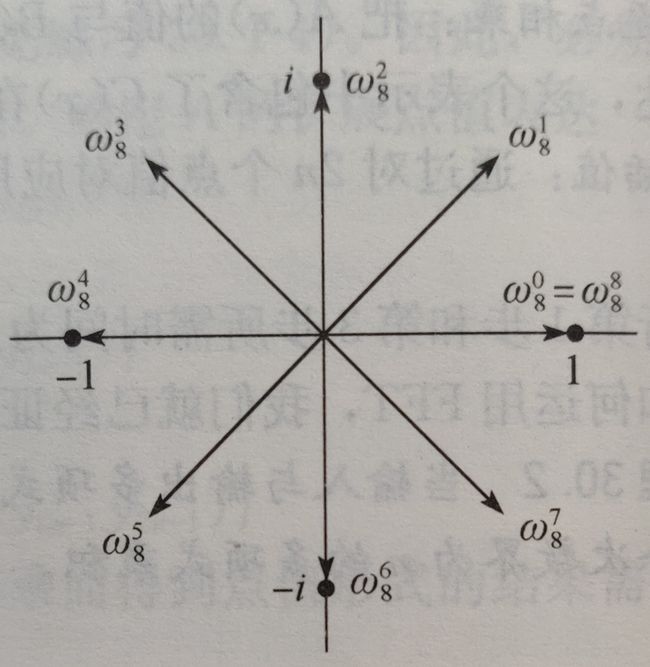

下面给出一些非常重要的结论(想理解深刻一点的的请自行推导)：
消去引理：对任何整数$n\ge 0,k\ge 0,$以及$d>0$有：$${\omega }_{dn}^{dk}={\omega }_n^k$$证明：$${\omega }_{dn}^{dk}=(e^{2\pi i/dn}{)}^{dk}=(e^{2\pi i/n}{)}^k={\omega }_n^k$$
推论：对任意偶数n>0，有$${\omega }_n^{n/2}={\omega }_2=-1$$证明：
$${\omega }_n^{n/2}=(e^{2\pi i/n}{)}^{n/2}=e^{\pi i}=(e^{2\pi i/8}{)}^4={\omega }_8^4=-1$$
折半引理：如果n>0为偶数，那么n个n次单位复数根的平方的集合就是n/2个n/2次单位复数根的集合。
证明：根据消去引理，对任意非负整数k，我们有$({\omega }_n^k{)}^2={\omega }_{n/2}^k$。注意，如果对所有n次单位复数根进行平方，那么获得每个n/2次单位根正好2次，因为：
$$({\omega }_n^{k+n/2}{)}^2={\omega }_n^{2k+n}={\omega }_n^{2k}{\omega }_n^n={\omega }_n^{2k}=({\omega }_n^k{)}^2$$因此，${\omega }_n^k$与${\omega }_n^{k+n/2}$平方相同，而且${\omega }_n^{k+n/2}=-{\omega }_n^k$。
最后一句话可以这么理解，(单位复数根的平方)等于(它乘以自身的n/2次方后得到的单位复数根的平方)，在复平面上这两点关于原点对称，等大反向(实部互为相反数)。因此用了折半引理之后，不相等的单位复数根数量就减半为n/2个。又因为平方过后的n/2个单位复数根满足${\omega }^{n/2}=1$，因此平方后的单位复数根就成了n/2次单位复数根而不再是n次单位复数根了。

DFT和FFT

通过使用一种称为快速傅里叶变换FFT的方法，利用单位复数根的特殊性质，我们就可以在$O(n\lg n)$时间内计算出$DF{T}_n(a)$。我们假设n恰好是2的整数倍(为什么这么假设请往后看)。
FFT利用了分治的策略，对于多项式$A(x)$：
$$A(x)=\sum _{j=0}^{n-1}{a}_j{x}^j=a_0+a_1{x}^1+a_2{x}^2+a_3{x}^3+...+a_{n-1}{x}^{n-1}$$分别提取$A(x)$中偶数下标的系数与奇数下标的系数：
$$\begin{gathered} A(x)=(a_0+a_2{x}^2+...+a_{n-2}{x}^{n-2})+(a_{1}x+a_3{x}^3+...+a_{n-1}{x}^{n-1}) \\ =(a_0+a_2{x}^2+...+a_{n-2}{x}^{n-2})+x(a_1+a_3{x}^2+...+a_{n-1}{x}^{n-2}) \end{gathered}$$分别定义两个新的次数界为n/2的多项式$A^{[0]}(x)$和$A^{[1]}(x)$：
$$A^{[0]}(x)=a_0+a_{2}x+a_4{x}^2+...+a_{n-2}{x}^{n/2-1}$$$$A^{[1]}(x)=a_1+a_{3}x+a_5{x}^2+...+a_{n-1}{x}^{n/2-1}$$于是有：
$$A(x)=A^{[0]}(x^2)+x{A}^{[1]}(x^2)$$设$k<\frac{n}{2}$，
把${\omega }_n^k$作为x代入A(x)有：
$$A({\omega }_n^k)=A^{[0]}({\omega }_n^{2k})+{\omega }_n^k{A}^{[1]}({\omega }_n^{2k})=A^{[0]}({\omega }_{n/2}^k)+{\omega }_n^k{A}^{[1]}({\omega }_{n/2}^k)\text{\hspace{1em}(1)}$$把${\omega }_n^{k+n/2}$作为x代入A(x)有：
$$\begin{gathered} A({\omega }_n^{k+n/2})=A^{[0]}({\omega }_n^{2k+n})+{\omega }_n^{k+n/2}{A}^{[1]}({\omega }_n^{2k+n})=A^{[0]}({\omega }_n^{2k}{\omega }_n^n)-{\omega }_n^k{A}^{[1]}({\omega }_n^{2k}{\omega }_n^n) \\ =A^{[0]}({\omega }_n^{2k})-{\omega }_n^k{A}^{[1]}({\omega }_n^{2k})=A^{[0]}({\omega }_{n/2}^k)-{\omega }_n^k{A}^{[1]}({\omega }_{n/2}^k)\text{\hspace{1em}(2)} \end{gathered}$$通过对比(1)(2)两式可以知道，$A({\omega }_n^k)$和$A({\omega }_n^{k+n/2})$仅仅相差一个符号。这意味着，如果我们知道了$A^{[0]}({\omega }_{n/2}^k)$和$A^{[1]}({\omega }_{n/2}^k)$的值，就能知道$A({\omega }_n^k)$和$A({\omega }_n^{k+n/2})$的值。
换句话说，如果我们知道了$A^{[0]}(x)$和$A^{[1]}(x)$分别在${\omega }_{n/2}^0,{\omega }_{n/2}^1,...,{\omega }_{n/2}^{n-1}$处的点值，就能求出$A(x)$在${\omega }_{n/2}^0,{\omega }_{n/2}^1,...,{\omega }_{n/2}^{n-1}$处的点值。
而对于$A^{[0]}(x)$和$A^{[1]}(x)$，我们同样可以应用这种分治的思想，将它们进行分治从而得到他们的值。分治的边界是n = 1，此时代入的是${\omega }_1^0$，得到的值即为$a_0$，最终时间复杂度：
$$T(n)=2T(\frac{n}{2})+O(n)=O(n\lg n)$$

IDFT和IFFT

点值表示转系数表示就是我们常说的求逆离散傅里叶变换的过程。即系数向量$a=(a_0,a_1,...,a_{n-1})$就是值向量$y=(y_0,y_1,...,y_{n-1})$的逆离散傅里叶变换。

记住一个结论：把多项式$A(x)$的离散傅里叶变换结果作为另一个多项式$B(x)$的系数，取单位根的倒数即${\omega }_n^0,{\omega }_n^{-1},{\omega }_n^{-2},...,{\omega }_n^{-(n-1)}$作为x代入$B(x)$，再将计算出的每个值除以n，得到的就是A(x)的各项系数。
不能理解的话看下面的矩阵：
$$\left[\begin{array}{c}y(x_0)\\ y(x_1)\\ y(x_2)\\ ...\\ y(x_{n-1})\end{array}\right]=\left[\begin{array}{ccccc}({\omega }_n^0{)}^0& ({\omega }_n^0{)}^1& ({\omega }_n^0{)}^2& ...& ({\omega }_n^0{)}^{n-1}\\ ({\omega }_n^1{)}^0& ({\omega }_n^1{)}^1& ({\omega }_n^1{)}^2& ...& ({\omega }_n^1{)}^{n-1}\\ ({\omega }_n^2{)}^0& ({\omega }_n^2{)}^1& ({\omega }_n^2{)}^2& ...& ({\omega }_n^2{)}^{2(n-1)}\\ ...& ...& ...& ...& ...\\ ({\omega }_n^{n-1}{)}^0& ({\omega }_n^{n-1}{)}^1& ({\omega }_n^{n-1}{)}^2& ...& ({\omega }_n^{n-1}{)}^{n-1}\end{array}\right]\left[\begin{array}{c}{a}_0\\ a_1\\ a_2\\ ...\\ a_{n-1}\end{array}\right]\text{\hspace{1em}(3)}$$我们记中间的大矩阵为V_n，构造矩阵$D_{i,j}=({\omega }_n^{-i}{)}^j$(即V中每一项取倒数)，则有：
$$D_n=\left[\begin{array}{ccccc}({\omega }_n^0{)}^0& ({\omega }_n^0{)}^1& ({\omega }_n^0{)}^2& ...& ({\omega }_n^0{)}^{n-1}\\ ({\omega }_n^{-1}{)}^0& ({\omega }_n^{-1}{)}^1& ({\omega }_n^{-1}{)}^2& ...& ({\omega }_n^{-1}{)}^{n-1}\\ ({\omega }_n^{-2}{)}^0& ({\omega }_n^{-2}{)}^1& ({\omega }_n^{-2}{)}^2& ...& ({\omega }_n^{-2}{)}^{(n-1)}\\ ...& ...& ...& ...& ...\\ ({\omega }_n^{-(n-1)}{)}^0& ({\omega }_n^{-(n-1)}{)}^1& ({\omega }_n^{-(n-1)}{)}^2& ...& ({\omega }_n^{-(n-1)}{)}^{n-1}\end{array}\right]$$
由矩阵乘法我们知道，因为$E_n=D_n\cdot V_n$，所以$V_n^{-1}=\frac{1}{n}{D}_n$。熟悉矩形的同学可能一下子就反应过来了，我们之所以取倒数再除以n，为的就是求中间矩阵的逆矩阵。我们将$\frac{1}{n}{D}_n$在等式(3)两侧左乘就能得到：
$$\left[\begin{array}{ccccc}({\omega }_n^0{)}^0& ({\omega }_n^0{)}^1& ({\omega }_n^0{)}^2& ...& ({\omega }_n^0{)}^{n-1}\\ ({\omega }_n^{-1}{)}^0& ({\omega }_n^{-1}{)}^1& ({\omega }_n^{-1}{)}^2& ...& ({\omega }_n^{-1}{)}^{n-1}\\ ({\omega }_n^{-2}{)}^0& ({\omega }_n^{-2}{)}^1& ({\omega }_n^{-2}{)}^2& ...& ({\omega }_n^{-2}{)}^{(n-1)}\\ ...& ...& ...& ...& ...\\ ({\omega }_n^{-(n-1)}{)}^0& ({\omega }_n^{-(n-1)}{)}^1& ({\omega }_n^{-(n-1)}{)}^2& ...& ({\omega }_n^{-(n-1)}{)}^{n-1}\end{array}\right]\left[\begin{array}{c}y(x_0)\\ y(x_1)\\ y(x_2)\\ ...\\ y(x_{n-1})\end{array}\right]=\left[\begin{array}{c}{a}_0\\ a_1\\ a_2\\ ...\\ a_{n-1}\end{array}\right]$$现在就很好理解那句结论的含义了。然而事实上，我们根本不用这么麻烦的去做，我们为单位复数根取倒数的过程，实际上就是求它的共轭复数(仅对模为1的复数有效)。

高效的FFT实现

二进制翻转

网上盗的图。

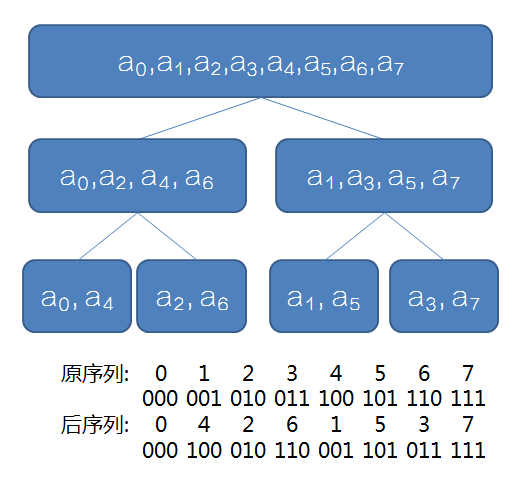
二进制翻转：将系数以n位二进数来表示，将末位提到首位，剩下的n - 1位左右翻转。如图有8个系数，就转为3位二进制，因为$2^3=8$。如果只有6个数呢？此时我们就需要补上$a_6=0,a_7=0$来凑出8个。
再举个例子，如果是14个系数，我们就要加入新的高阶项直到$2^4=16$个。对于第10个数$a_9$来说，其4位二进制是1001，末位提前，变为1-100，剩下的n - 1 = 3位左右翻转成001。即可得到$a_9$翻转后的数应为1001即$a_9$。怎么样，是否理解了呢？
我们只需要预处理每一个数的二进制位翻转后的结果，并在 FFT 开始前交换所有数与他翻转之后的数。

蝴蝶操作

看看前面推导出来的等式：
$$A({\omega }_n^k)=A^{[0]}({\omega }_{n/2}^k)+{\omega }_n^k{A}^{[1]}({\omega }_{n/2}^k)\text{\hspace{1em}(1)}$$$$A({\omega }_n^{k+n/2})=A^{[0]}({\omega }_{n/2}^k)-{\omega }_n^k{A}^{[1]}({\omega }_{n/2}^k)\text{\hspace{1em}(2)}$$我们可以看到，(1)(2)两式中都做了${\omega }_n^k$乘上$A^{[1]}({\omega }_{n/2}^k)$这一操作，在(1)式中$A^{[0]}({\omega }_{n/2}^k)$加上它，在(2)式中$A^{[0]}({\omega }_{n/2}^k)$减去它。我们把这种正负数形式都出现过的的因子称为旋转因子。实际上我们完全可以定义一个中间变量来保存这个值，这样就不用每次都计算一次乘积。这就是蝴蝶操作，这样解释是不是就简单多了呢？

实例

好了，FFT的介绍就到这里啦。希望本篇博客对于同学们有一定的帮助，喜欢的话请一定要点个赞哦，不喜欢的话也请在评论区指出问题，大家一起改正。我的代码是为了方便同学们理解而写的通用版，而事实上你们应用时，完全只需要记住函数的部分。main函数中的操作你们自己去决定，就比如有的博客用字符串读取多项式也是可取的。只要保证得到系数就好了。

#include 
#include 
#include 
#include 
using namespace std;

const double PI = acos(-1.0); // 定义常数Pi
const int maxLen = 2097153; // 定义数组最大长度常数

char strA[maxLen], strB[maxLen]; // 存放系数字符串
complex<double> A[maxLen], B[maxLen]; // 多项式数组要全局声明，因为栈的空间是不够的
complex<double> omega[maxLen], recip[maxLen]; // 预处理单位复数根和其倒数并存放在数组中

int binR[maxLen]; // binR数组存放翻转后的数
int coef[maxLen];
int bits = 0, len = 1; // bits是二进制位数，len是次数界，len = 2^bits

void BinaryRotate() // 二进制翻转函数
{
	for (int i = 0; i < len; i++)
    {
        binR[i] = (binR[i >> 1] >> 1) | ((1 & 1) << (bits - 1));
        cout << binR[i] << endl;
    }
}

void ComputeRoot() // 计算单位复数根函数
{
	for (int i = 0; i < len; i++)
	{
		omega[i] = complex<double>(cos(2 * PI * i / len), sin(2 * PI * i / len));
		recip[i] = conj(omega[i]); // conj是一个头文件自带的求共轭复数的函数，精度较高。当复数模为1时，共轭复数等于倒数
	}
}

void FFT(complex<double> *p, complex<double> *q)
{
	for (int i = 0; i < len; i++)
		if (binR[i] > i)
			swap(p[binR[i]], p[i]);

	complex<double> temp;
	for (int j = 2; j < len; j *= 2) // 自底向上，每次都是
	{
		int tempLen = j / 2; // tempLen就是分治的过程，即文章中的k/2
		for (complex<double>* r = p; r != p + len; p += tempLen)
		{
			for (int i = 0; i < tempLen; i++)
			{
				temp = q[len / j * i] * r[i + tempLen];// 蝴蝶操作
				r[i + tempLen] = r[i] - temp;
				r[i] = r[i] + temp;
			}
		}
	}
}

int main(void)
{
	int lenA, lenB; // lenA，lenB分别表示多项式A，B的最大次数
	cout << "请分别输入多项式A，B的系数个数" << endl;
	cin >> lenA >> lenB;

	// 寻找大于lenA+lenB的最小的2的n次方，bits用来记录二进制位数
	for (; len <= lenA + lenB; len *= 2, bits++);
	BinaryRotate(); // 预置好分治后的数

	cout << "请输入多项式A系数" << endl;
	for (int i = 0; i < lenA; i++) // 分别输入多项式A，B的系数
		scanf("%lf", &A[i].real());
    cout << "请输入多项式B系数" << endl;
	for (int i = 0; i < lenB; i++)
		scanf("%lf", &B[i].real());

	FFT(A, omega);// 系数表示转点值表示
	FFT(B, omega);
	for (int i = 0; i < len; i++) // 点值相乘
		A[i] *= B[i];
	FFT(A, recip); // 点值表示转系数表示

	for (int i = 0; i < len; i++)
		printf("A[%d]:%lf", i, A[i].real());

}