手推SVM（一）-数学推导

1. SVM的想法
2. SVM中在数学上目标
   2.1 判定条件
   2.2 最大间隔假设
3. SVM的推导
   3.1 第一种境界
   3.2 第二种境界
   3.3 第三种境界-kkt条件

SVM的推导过程和他的地位一样重要，虽然很久以前就已经接触过SVM了，但总感觉理解不是很深，接着听课的热度，顺便写篇文章让自己理解更深刻一点，本文假设你只会简单的向量乘法，推导出SVM。

1.SVM的想法

监督学习，作为一个二分类任务，在平面上表示就是希望有这么一条分类边界，能把正负样本分开，每种分类器画的分类边界都不一样，到底哪个最好，只能看问题，看数据，看实际的应用场景。

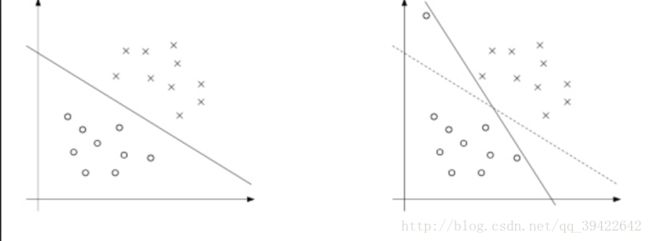
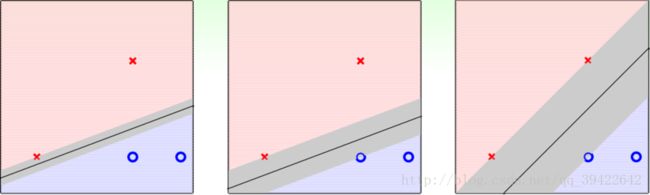
上图中，有三条决策边界，而SVM的关键假设是 ：找到一条直线到样本点两边的距离最大,也就是margin最大。这样的好处就是模型具有更好的鲁棒性。

什么是鲁棒性呢？
通俗理解来说就是更能容忍误差，比如下图中的红色xx,从左到右是点到直线的距离越来越远的，如果是最左边的一条线，假设有一个点和红色叉叉比较接近，但刚好在红色叉叉的下方，这时候，模型会判定这条线蓝色小圈圈的，而最右边的那条线则会判定为红色叉叉，所以相比来说，最右边的线比最左边的线具有更好的鲁棒性。

上图是点到线的距离，那换成线到点的距离是不是一样的呢？

很容易想到我们希望这条街的街宽最大，但是，该怎么定义呢？

用数学表达式表达出来可以有这样的式子，街宽用术语来说就是margin:

OK，这是我们的想法，那我们怎么实现这个想法呢？

2.SVM中在数学上目标

2.1 判定条件

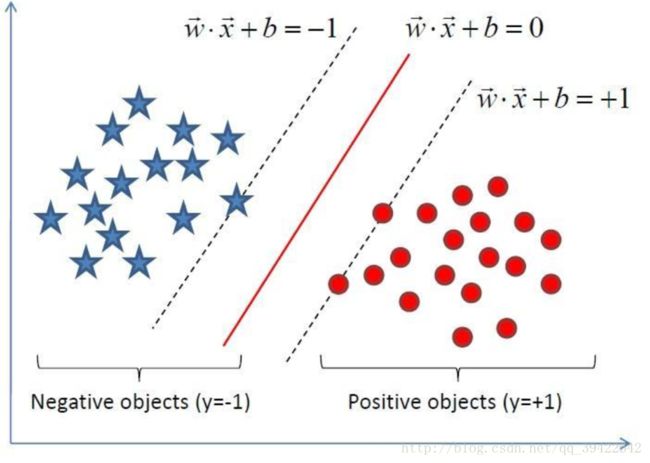
假设中间那条实线是最好的决策边界，做 w⃗  为垂直于中间那条线的向量，新来一个点，与0组成向量表示为 u⃗  ,如果 u⃗  在 w⃗  上的投影大于某一数值C，则判定该点为正样本，用向量表示为:

w⃗ ||w||→∗u⃗ >=C

把C移过来可以写成：

1||w||→(w⃗ ∗u⃗ +b)>=0

2.2 最大间隔假设

为了让决策边界更好的划分样本，也为了模型具有更好的泛化能力，我们希望模型在训练集中，这条街的宽度尽可能大，同时，因为 1||w||→ 是可变的，对整体的公式没有影响，相当于系数，用数学公式表达这个想法就是:

w⃗ ∗X+→+b>=1

w⃗ ∗X−→+b<=−1

当然这个1不是规定的，也可以是更大的数，但如果是10，我总能够对方向量 w⃗  进行适当的伸缩，让它又变回1，所以为了计算方便，我们把它设成1.这就是SVM的最大间隔假设。

再来回顾一下，我们的总目标就是找到这样参数 w⃗ ,b 能判断样本是正样本还是负样本，同时在训练集中，要求它的间隔尽可能得大。

1. SVM的推导

3.1 第一种境界

提个要求很容易，但具体的参数应该怎么求呢？
为了求解方便，我们用一个小技巧，把最大间隔假设合成一个式子：

yi(w⃗ ∗X+→+b)>=1，yi=1,−1

其实这里的 yi 相当于一个符号，其中对于边界上的点（街边）要求：

yi(w⃗ ∗X⃗ +b)=1

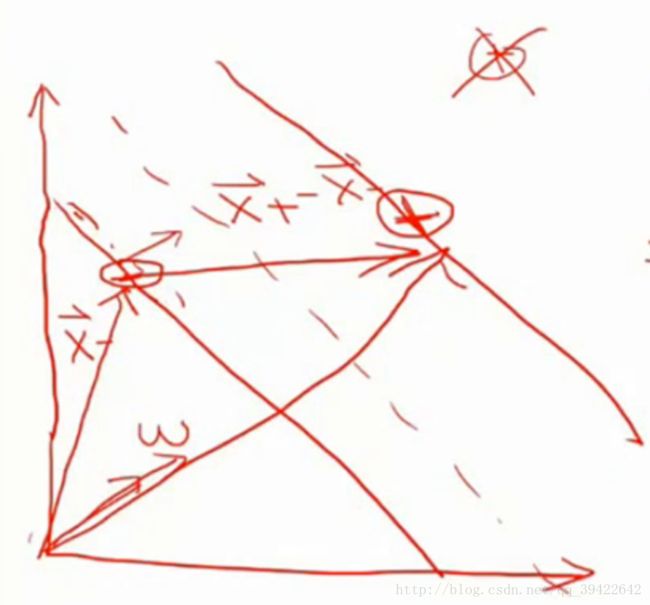
那这个街宽应该怎么求出来呢？假设我们只会向量的乘法，我们来看一下怎么通过向量的乘法求出街的宽度。

下方为负样本，上方为正样本，在法向量 w⃗  上选取位于街边的正样本，可以得到正，负样本的距离为

向量 x+→−x_→的模：|x+→−x_→|

,那街的宽度不就是向量 x+→−x_→ 在法向量上的投影吗？

width=(x+→−x_→)∗w⃗ ||w⃗ ||=x+→∗w⃗ ||w⃗ ||−x−→∗w⃗ ||w⃗ ||

=1−b||w⃗ ||−−(1−b)||w⃗ ||=2||w⃗ ||

这样就得到我们优化的目标了，他越大就越好，所以我们机器学习的任务就变成了如何最大化这个目标函数了。

L=max2||w⃗ ||→max1||w⃗ ||→min ||w⃗ ||→min12||w⃗ ||2

其实这个二分之一就是为了求导方便。

由此就可以得到这么一个约束条件：

L=min12||w⃗ ||2

yi(w⃗ ∗X+→+b)=1

那一般情况拿着这样一个优化问题给做优化的人来做就OK了。

3.2 第二种境界

如果我们没有把问题留给数学系的朋友来求解，我们继续再来推一下看能不能推出什么东西来。
用拉格朗日乘子法求上式的最小值

L=12||w⃗ ||2−∑αi[yi(w⃗ ∗Xi→+b)−1](1)

有：

SVM=minb,w(maxall αi>=0L(b,w,α))

这样子直接求L的最大值不好求，所以我们把它转成对偶问题 ,因为对于任何的 α′>=0 ,永远存在一个 α 使得 maxα>=0L(b,w,α)≥L(b,w,α′) ,所以有：

minb,w(maxall αi>=0L(b,w,α))≥minb,wL(b,w,α′)

然后在右式再加一个max依然成立：

minb,w(maxall αi>=0L(b,w,α))≥maxall α′≥0(minb,wL(b,w,α′))

因为 αi 只是一个符号，我们把它再换回来，可以得到：

minb,w(maxall αi>=0L(b,w,α))≥maxall α≥0(minb,wL(b,w,α))

就得到了左式的对偶问题是右式，主要是做 min,max 交换。
原来解左边的问题，比较麻烦，但是转换为对偶问题后，对偶问题的里面是个最小化问题，这样就比较好解了。

接着化简一下：

求偏导：∂L∂w⃗ =w⃗ −∑αiyiX⃗ i=0

w⃗ =∑αiyiX⃗ i(2)

再对b求偏导：∂L∂b=∑αiyi=0(3)

然后将（2），（3）两式再代入（1）式，得：

L=12∑αiyiX⃗ i∗∑αjyjX⃗ j−∑αiyiX⃗ i∗(∑αjyjX⃗ j)−∑αiyib+∑αi

又因为b为常数，所以 b∗∑αiyi=0(由（3）可得)， 这里的 i,j 均为 0−n 之间的数，n表示样本数，所以求和时 i,j 所代表的都是一样的意思。对这个式子化简可得：

L=∑αi−12∑αiyiX⃗ i∗∑αjyjX⃗ j=∑αi−∑∑αiαjyiyjX⃗ iX⃗ j

这个是我们今天最大的发现，原来这个L居然仅仅取决于训练集中两两样本的点乘。

再把 w⃗ ,b 代入决策边界：

w⃗ ∗u⃗ +b>=0

∑αiyiX⃗ i∗u⃗ +b>=0

其实预测的时候，预测的样本就放在 u⃗  那里，其中 αi 大于0时，就是所谓的支持向量（证明看下面），同时与它对应的 X⃗ i 都在街边，接下来用优化的方法来做优化就OK了。

3.3 第三种境界-kkt条件

经过我们的推导，发现最后的化简式子里，已经把 b,w⃗  都消除了，但是，他们是模型的系数，是我们要优化的参数，而 α 只是求解化简过程中的中间变量，也是上式能优化的参数，那 b,w⃗  该怎么办呢？

既然上面能求出最优的 α ，那能否通过 α 求出最优的 b,w⃗  呢？那是当然的，不然SVM也无法占领机器学习界那么久。

在求解优化问题中，又一个条件称为kkt条件，用在这里，根据前面的推导，对于 b,w⃗ ,α 的优化问题：$$

• primal feasible:
  yi(w⃗ ∗X⃗ +b)≥1(1)
• dual feasible:
  αi≥0(2)
• dual-inner optimal:
  αiyi=0;w⃗ =∑αiyiX⃗ i(3)
• primal-inner optimal:
  αi[yi(w⃗ ∗Xi→+b)−1]=0(4)

当已知 α 求 w⃗  很容易，代入到(3)式就OK了。
主要看一下b怎么得到，看一下和b有关的只有两条式子，分别是(1),(4),如果用(1)的话，只能得到一个区间，所以用（4），那（4）该怎么使用呢？

由条件(2)可以看到 αi≥0 , αi=0 ，等式恒成立，如果 αi>0 ,则要等式成立，必须有 yi(w⃗ ∗Xi→+b)−1=0 ,又 yi 为{+1,-1}，两边乘以 yi 有

b=yi−(w⃗ X⃗ i)

如此，就顺利求出b了。

• 问个小问题：如果有5566个样本，1126个支持向量，有多少个样本在最优边界上呢？看完总结就知道了。

总结一下，这篇文章主要讲解了理解SVM的三个层次，每一层都是逐渐加深理解的。通过最大化软间隔，得到一开始的优化问题，接着运用拉格朗日乘子法和对偶问题求最优化问题的解，得到最优的 α ,通过最优的 α 求解出最优的 b,w ,如果 αi>0 ,则对应的点 (X⃗ i,yi) 在边界上，我们称这样的点为支撑向量，因为支撑向量总是在最优边界上的，所以对于上面那个问题，应该是：

1126<位于最优边界上的样本<5566

第二版
2017.12.7
增加对支持向量的理解和kkt条件