让你看懂聚类分析

目录

1.聚类分析概述
2.各种距离的定义
2.1 样本相似性度量
2.2 类与类间的相似性度量
2.3 变量间的相似度度量
3.划分聚类
4.层次聚类

1.聚类分析概述

聚类分析是一种定量方法，从数据分析的角度看，它是对多个样本进行定量分析的多元统计分析方法，可以分为两种：

• 对样本进行分类称为Q型聚类分析
• 对指标进行分类称为R型聚类分析

从数据挖掘的角度看，又可以大致分为四种：

• 划分聚类
• 层次聚类
• 基于密度的聚类
• 基于网格的聚类

本篇文章将从数据挖掘的角度来揽述，但也会借鉴数学建模的部分思想。

无论是从那个角度看，其基本原则都是：
希望族（类）内的相似度尽可能高，族（类）间的相似度尽可能低（相异度尽可能高）。

先来看一下从数据挖掘的角度看，这四种聚类方法有什么不同。

划分聚类：给定一个n个对象的集合，划分方法构建数据的k 个分区，其中每个分区表示一个族（族）。大部分划分方法是基于距离的，给定要构建的k个分区数，划分方法首先创建一个初始划分，然后使用一种迭代的重定位技术将各个样本重定位，直到满足条件为止。

层次聚类：层次聚类可以分为凝聚和分裂的方法；凝聚也称自底向上法，开始便将每个对象单独为一个族，然后逐次合并相近的对象，直到所有组被合并为一个族或者达到迭代停止条件为止。分裂也称自顶向下，开始将所有样本当成一个族，然后迭代分解成更小的值。

基于密度的聚类：其主要思想是只要“邻域“中的密度（对象或数据点的数目）超过某个阀值，就继续增长给定的族。也就是说，对给定族中的每个数据点，在给定半径的邻域中必须包含最少数目的点。这样的主要好处就是过滤噪声，剔除离群点。

基于网格的聚类：它把对象空间量化为有限个单元，形成一个网格结构，所有的聚类操作都在这个网格结构中进行，这样使得处理的时间独立于数据对象的个数，而仅依赖于量化空间中每一维的单元数。

划分聚类是基于距离的，可以使用均值或者中心点等代表族中心，对中小规模的数据有效；而层次聚类是一种层次分解，不能纠正错误的合并或划分，但可以集成其他的技术；基于密度的聚类可以发现任意形状的族，族密度是每个点的“邻域“内必须具有最少个数的点，可以过滤离群点；基于网格的聚类使用一种多分辨率网格数据结构，能快速处理数据。

但在目前的工业应用中，主要是划分聚类和层次聚类的应用，所以接下来的内容主要在这几个方面。

2.各种距离的定义

2.1 样本相似性度量
要用数量化的方法对事物进行分类，就要用数量化的方法来定义每个样本的相似程度，这个相似程度在数学上可以称之为距离，最常用的闵氏距离：

dp(x,y)=[∑k=1p|xk−yk|q]1q

当 q=1,2,或者q→+∞ 时，可以分别得到：

绝对值距离：d1(x,y)=[∑k=1p|xk−yk|](1)

欧几里得距离：d2(x,y)=[∑k=1p|xk−yk|2]12(2)

切比雪夫距离：d∞(x,y)=max1≤k≤p|xk−yk|(3)

其中最常用的又是欧式距离，因为当坐标轴进行正交旋转的时候，欧式距离是保持不变的，而很多算法，都是需要变换坐标轴的。

• 缺点1：闵氏距离没有考虑样本的各指标的数量级水平。当样本的各指标数量级相差悬殊时，该距离不合适。

• 解决方法：在计算距离之前，先把所有指标都转化为统一的分布内，即标准化。

• 缺点2:使用欧式距离要求各坐标对距离的贡献应该是同等的，且变差大小也是相同的，如果变差不同，则不太适用。
  比如在择偶时衡量一个男性的指标，假如是身高和收入水平，一个人是1.5米，收入6000，另一个人是1.8米，收入5500，这两个人的两个指标的变差差别就很大，不好用欧式距离。

• 解决方法2:将欧式距离进行一定的改写：

  d2(xik,xjk)=[∑k=1p（xik−xjkskk）2]12
  其中 skk 表示变量k的标准差，其实就是为了调整变量的变差。

与闵氏距离相似的还有马氏距离，它是对闵氏距离的进一步调优：

d2ij(M)=(Xi−Xj)Tϵ−1(Xi−Xj)

其中 ϵ−1 表示协方差矩阵的逆，可以证明它对一切线性变换是不变的，故不受量纲的影响，它不仅对自身的变差做了调整，还对指标的相关性也做了考虑，非常适用于两个未知样本集的相似度计算。

2.2 类与类间的相似性度量
如果有两个样本类 G1,G2 ,可以用下面的一系列方法度量他们之间的距离：

最短距离法：D(G1,G2)=minxi∈G1yi∈G2{d(xi,yi)}(2.2.1)

直观理解为两个类中最近两点之间的距离。

最长距离法：D(G1,G2)=maxxi∈G1yi∈G2{d(xi,yi)}(2.2.2)

直观理解为两个类中最远离两点间的距离

重心法：D(G1,G2)=d(x⎯⎯,y⎯⎯)(2.2.3)

x⎯⎯,y⎯⎯ 分别为两个族的重心。

类平均法：D(G1,G2)=1n1n2∑xi∈G1∑xj∈G2d(xi,xj)(2.2.4)

它表示两个样本点距离的平均， n1,n2 分别为 G1,G2 中的样本点个数。

离差平方和法：D(G1,G2)=D12−D1−D2(2.2.5)

其中

D1=∑xi∈G1(xi−x1⎯⎯⎯⎯)T(xi−x1⎯⎯⎯⎯),D2=∑xi∈G2(xi−x2⎯⎯⎯⎯)T(xi−x2⎯⎯⎯⎯)

D12=∑xi∈G1UG2(xi−x⎯⎯)T(xi−x⎯⎯)

式中

x⎯⎯1=1n1∑xi∈G1xi,x⎯⎯2=1n2∑xj∈G2xj,x⎯⎯=1n1+n2∑xk∈G1UG2xk

若 G1,G2 内部点与点距离很小，则它们能很好地各自聚为一类，并且这两类又能充分分离（ D12 很大）,这是D就很大。

2.3 变量间的相似度度量

相关系数，记变量 xj 的取值 （x1j,x2j,⋯,xnj） 就可以用两变量的相关系数作为他们的相似性度量:

rjk=∑i=1n(xij−x⎯⎯j)(xik−x⎯⎯k)[∑i=1n(xij−x⎯⎯j)2(xik−x⎯⎯k)2]12(2.3.1)

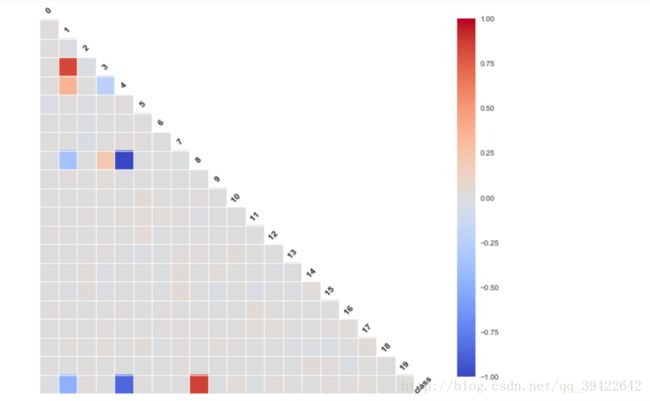
在监督学习中，如果特征数量少，可以使用相关系数筛选有用特征，python代码也很简单:

plt.figure(figsize=(12,12))
from seaborn.linearmodels import corrplot,symmatplot

_ = corrplot(df,annot = False)
plt.show()

余弦相似度：也可以利用两个变量的夹角余弦作为它们的相似性度量：

rjk=∑i=1nxijxik[∑i=1nx2ij∑i=1nx2ik]12

两者都满足

• |rjk|≤1,对一切的j,k
• rjk=rkj,对一切的j,k

其中 |rjk| 越接近1， xj,xk 就越相似，如果越接近0，相似性就越弱。

更多距离度量公式点我

3.划分聚类

对于给定的类目数据k，首先给出初始划分，通过迭代改变样本和族的隶属关系，使得每次划分都比前一次好，直到隶属关系基本稳定。

划分聚类的代表是K-Means算法，它需要在一开始指定类目数，根据距离最近的原则，把待分类的样本点划分到不同的族，然后按照平均法计算各个族的质心，重新分配质心，直到质心的移动距离小于某个值。

3.1 k均值聚类

K-Means算法也称K-均值聚类算法，是一种广泛使用的聚类算法，也是其他聚类算法的基础。

假定输入样本为S = X1,X2,···，Xm,则算法步骤为：
1. 选择初始的k个类别中心μ1μ2…μk

2. 对于每个样本Xi，将其标记为距离类别中心最近的类别（距离计算一般采用欧式距离）
3. 将每个类别中心更新为隶属该类别的所有样本的均值
4. 重复最后两步，直到类别中心的变化小于某阈值。

终止条件一般有迭代次数，族中心变化率，最小平方误差MSE （Minimum Squared Error）等。

它的迭代过程如下：

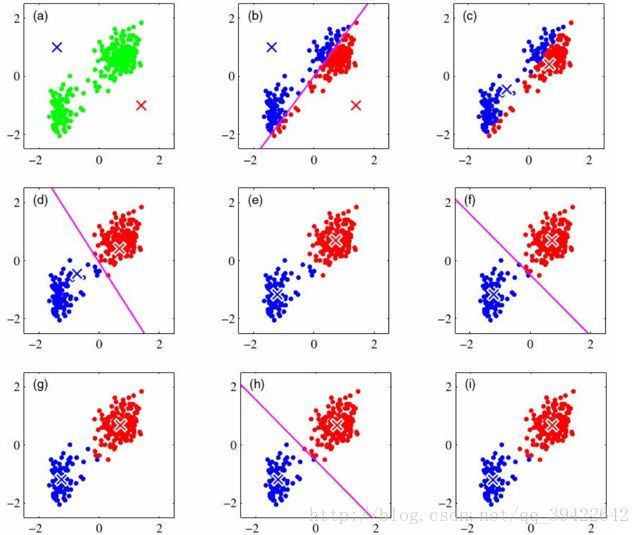
算法缺陷：k个族心初始点需要提前设定好，但现实情况中，不同场景下的k个族质心往往相差很大，在k值不会太大，应用场景不明确是，可以通过迭代求解损失函数最小时对应的k值。不同的随机种子点得到的结果完全不同，

看一下k=3得到的三种不同结果：



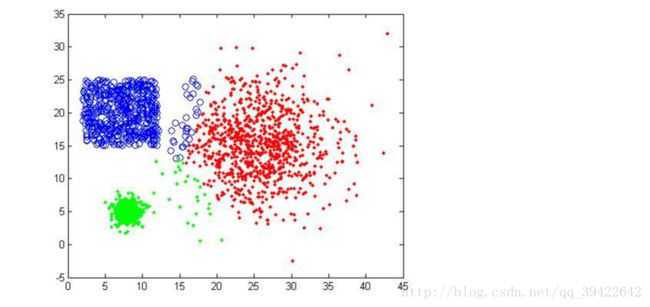
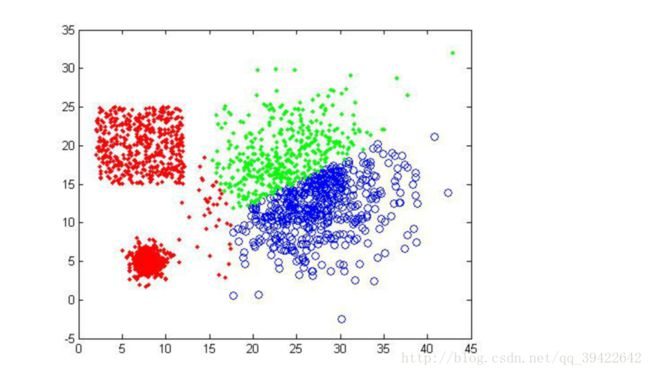
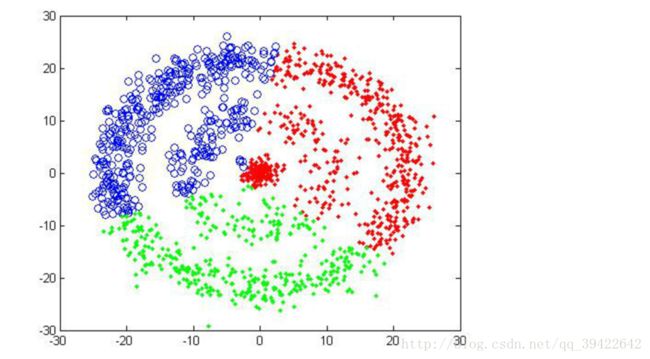
可以发现，即使k=3相同，但开始的情况不同，仍然有可能使得聚类不成功。第二张图就是聚类失败的例子。

4.层次聚类

层次聚类不需要指定类数，它把每个点划分为一族，将最近的两个点划分为一族，重复划分直到只剩下一个族。

用最短距离法看一下具体是怎么算的；

• 设又五个销售员， w1,w2,w3,w4,w5 ,他们的销售业绩由二维变量 v1,v2 描述，见表

记销售员 wi(i=1,2,3,4,5) 的销售业绩为 (vi1,vi2) ,使用绝对值距离来测量点与点之间的距离，使用最短距离法来测量类与类之间的距离，即

d(wi,wj)=∑k=12|vik−vjk|;D(Gp,Gq)=minwi∈Gpwj∈Gq{d(wi,wj)}

由距离公式可以算出距离矩阵：

• 第一步，所有的元素自成一类 H1={w1,w2,w3,w4,w5}. 每个类的平台高度为0，即 f(wi)=0,i=1,2,3,4,5. 显然，这时 D(Gp,Gq)=d(wp,wq)
• 第二步，取新类的平台高度为1，把 w1,w2 合成一个新类 h6 ,此时的分类情况是：
  H2={h6,w3,w4,w5}
• 第三步，取新类的平台高度为2，把 w3,w4 合成一个新类 h7 ，此时的分类情况是：
  H3={h6,h7,w5}
• 第四步，取新类的平台高度为3，把 h6,h7 合成一个新类 h8 ,此时的分类情况是：
  H4={h8,w5}
• 第五步，取新类的平台高度为4，把 h8.w5 合成一个新类 h9 ,此时的分类情况是:
  H5={h9}

如此就把所有的样本点聚为一类，如果想要聚成3类，完全可以在 H3 处停止迭代就OK了。用图可以表示为：

由此判断五个推销员中 w5工作最佳，w3,w4较好，w1,w2较差。 也就是三类。

参考
多元统计分析-何晓群
数学建模原理与应用
数据挖掘概念与技术