(计算机图形学)Delaunay三角形剖分的HTML+js的浏览器实现
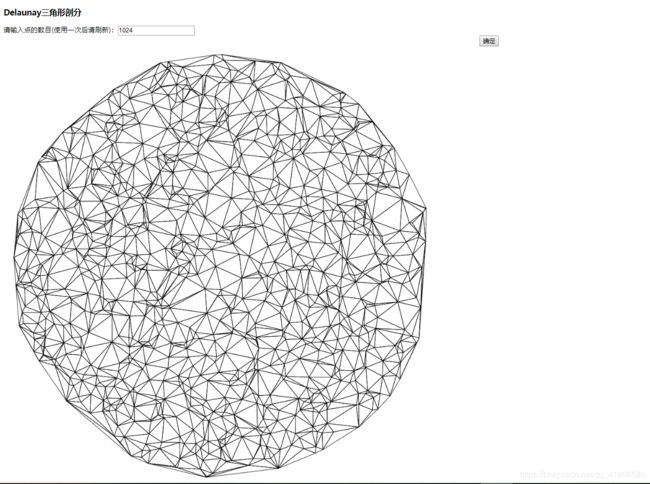
最近在学计算机图形学,第一次比较难的作业就是Delaunay三角形剖分,在这里记录一下代码。
HTML部分
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Delaunay三角形剖分</title>
</head>
<body>
<div class="b">
<h3>Delaunay三角形剖分</h3>
请输入点的数目(使用一次后请刷新):<input maxlength="4" value="2048" id="f" /><br />
<div align="center">
<input type="button" id="btn" value="确定" onclick="cs('f')" />
</div>
</div>
<canvas id="canvas" width="1024" height="1024">
</canvas>
<script type="text/javascript" src="delaunay.js">
</script>
<script type="text/javascript">
function cs(f) {
var f = document.getElementById(f).value;
var canvas = document.getElementById("canvas"),
ctx = canvas.getContext("2d"),
vertices = new Array(2048);
vertices.length=f;
var i, x, y;
for(i = vertices.length; i--; ) {
do {
x = Math.random() - 0.5;
y = Math.random() - 0.5;
} while(x * x + y * y > 0.25);
x = (x * 0.96875 + 0.5) * canvas.width;
y = (y * 0.96875 + 0.5) * canvas.height;
vertices[i] = [x, y];
}
console.time("triangulate");
var triangles = Delaunay.triangulate(vertices);
console.timeEnd("triangulate");
for(i = triangles.length; i; ) {
ctx.beginPath();
--i; ctx.moveTo(vertices[triangles[i]][0], vertices[triangles[i]][1]);
--i; ctx.lineTo(vertices[triangles[i]][0], vertices[triangles[i]][1]);
--i; ctx.lineTo(vertices[triangles[i]][0], vertices[triangles[i]][1]);
ctx.closePath();
ctx.stroke();
}
}
</script>
</body>
</html>
delaunay.js部分
var Delaunay;
(function() {
"use strict";
var EPSILON = 1.0 / 1048576.0;
function supertriangle(vertices) {
var xmin = Number.POSITIVE_INFINITY,
ymin = Number.POSITIVE_INFINITY,
xmax = Number.NEGATIVE_INFINITY,
ymax = Number.NEGATIVE_INFINITY,
i, dx, dy, dmax, xmid, ymid;
for(i = vertices.length; i--; ) {
if(vertices[i][0] < xmin) xmin = vertices[i][0];
if(vertices[i][0] > xmax) xmax = vertices[i][0];
if(vertices[i][1] < ymin) ymin = vertices[i][1];
if(vertices[i][1] > ymax) ymax = vertices[i][1];
}
dx = xmax - xmin;
dy = ymax - ymin;
dmax = Math.max(dx, dy);
xmid = xmin + dx * 0.5;
ymid = ymin + dy * 0.5;
return [
[xmid - 20 * dmax, ymid - dmax],
[xmid , ymid + 20 * dmax],
[xmid + 20 * dmax, ymid - dmax]
];
}
function circumcircle(vertices, i, j, k) {
var x1 = vertices[i][0],
y1 = vertices[i][1],
x2 = vertices[j][0],
y2 = vertices[j][1],
x3 = vertices[k][0],
y3 = vertices[k][1],
fabsy1y2 = Math.abs(y1 - y2),
fabsy2y3 = Math.abs(y2 - y3),
xc, yc, m1, m2, mx1, mx2, my1, my2, dx, dy;
/* Check for coincident points */
if(fabsy1y2 < EPSILON && fabsy2y3 < EPSILON)
throw new Error("Eek! Coincident points!");
if(fabsy1y2 < EPSILON) {
m2 = -((x3 - x2) / (y3 - y2));
mx2 = (x2 + x3) / 2.0;
my2 = (y2 + y3) / 2.0;
xc = (x2 + x1) / 2.0;
yc = m2 * (xc - mx2) + my2;
}
else if(fabsy2y3 < EPSILON) {
m1 = -((x2 - x1) / (y2 - y1));
mx1 = (x1 + x2) / 2.0;
my1 = (y1 + y2) / 2.0;
xc = (x3 + x2) / 2.0;
yc = m1 * (xc - mx1) + my1;
}
else {
m1 = -((x2 - x1) / (y2 - y1));
m2 = -((x3 - x2) / (y3 - y2));
mx1 = (x1 + x2) / 2.0;
mx2 = (x2 + x3) / 2.0;
my1 = (y1 + y2) / 2.0;
my2 = (y2 + y3) / 2.0;
xc = (m1 * mx1 - m2 * mx2 + my2 - my1) / (m1 - m2);
yc = (fabsy1y2 > fabsy2y3) ?
m1 * (xc - mx1) + my1 :
m2 * (xc - mx2) + my2;
}
dx = x2 - xc;
dy = y2 - yc;
return {i: i, j: j, k: k, x: xc, y: yc, r: dx * dx + dy * dy};
}
function dedup(edges) {
var i, j, a, b, m, n;
for(j = edges.length; j; ) {
b = edges[--j];
a = edges[--j];
for(i = j; i; ) {
n = edges[--i];
m = edges[--i];
if((a === m && b === n) || (a === n && b === m)) {
edges.splice(j, 2);
edges.splice(i, 2);
break;
}
}
}
}
Delaunay = {
triangulate: function(vertices, key) {
var n = vertices.length,
i, j, indices, st, open, closed, edges, dx, dy, a, b, c;
/* Bail if there aren't enough vertices to form any triangles. */
if(n < 3)
return [];
/* Slice out the actual vertices from the passed objects. (Duplicate the
* array even if we don't, though, since we need to make a supertriangle
* later on!) */
vertices = vertices.slice(0);
if(key)
for(i = n; i--; )
vertices[i] = vertices[i][key];
/* Make an array of indices into the vertex array, sorted by the
* vertices' x-position. Force stable sorting by comparing indices if
* the x-positions are equal. */
indices = new Array(n);
for(i = n; i--; )
indices[i] = i;
indices.sort(function(i, j) {
var diff = vertices[j][0] - vertices[i][0];
return diff !== 0 ? diff : i - j;
});
/* Next, find the vertices of the supertriangle (which contains all other
* triangles), and append them onto the end of a (copy of) the vertex
* array. */
st = supertriangle(vertices);
vertices.push(st[0], st[1], st[2]);
/* Initialize the open list (containing the supertriangle and nothing
* else) and the closed list (which is empty since we havn't processed
* any triangles yet). */
open = [circumcircle(vertices, n + 0, n + 1, n + 2)];
closed = [];
edges = [];
/* Incrementally add each vertex to the mesh. */
for(i = indices.length; i--; edges.length = 0) {
c = indices[i];
/* For each open triangle, check to see if the current point is
* inside it's circumcircle. If it is, remove the triangle and add
* it's edges to an edge list. */
for(j = open.length; j--; ) {
/* If this point is to the right of this triangle's circumcircle,
* then this triangle should never get checked again. Remove it
* from the open list, add it to the closed list, and skip. */
dx = vertices[c][0] - open[j].x;
if(dx > 0.0 && dx * dx > open[j].r) {
closed.push(open[j]);
open.splice(j, 1);
continue;
}
/* If we're outside the circumcircle, skip this triangle. */
dy = vertices[c][1] - open[j].y;
if(dx * dx + dy * dy - open[j].r > EPSILON)
continue;
/* Remove the triangle and add it's edges to the edge list. */
edges.push(
open[j].i, open[j].j,
open[j].j, open[j].k,
open[j].k, open[j].i
);
open.splice(j, 1);
}
/* Remove any doubled edges. */
dedup(edges);
/* Add a new triangle for each edge. */
for(j = edges.length; j; ) {
b = edges[--j];
a = edges[--j];
open.push(circumcircle(vertices, a, b, c));
}
}
/* Copy any remaining open triangles to the closed list, and then
* remove any triangles that share a vertex with the supertriangle,
* building a list of triplets that represent triangles. */
for(i = open.length; i--; )
closed.push(open[i]);
open.length = 0;
for(i = closed.length; i--; )
if(closed[i].i < n && closed[i].j < n && closed[i].k < n)
open.push(closed[i].i, closed[i].j, closed[i].k);
/* Yay, we're done! */
return open;
},
contains: function(tri, p) {
/* Bounding box test first, for quick rejections. */
if((p[0] < tri[0][0] && p[0] < tri[1][0] && p[0] < tri[2][0]) ||
(p[0] > tri[0][0] && p[0] > tri[1][0] && p[0] > tri[2][0]) ||
(p[1] < tri[0][1] && p[1] < tri[1][1] && p[1] < tri[2][1]) ||
(p[1] > tri[0][1] && p[1] > tri[1][1] && p[1] > tri[2][1]))
return null;
var a = tri[1][0] - tri[0][0],
b = tri[2][0] - tri[0][0],
c = tri[1][1] - tri[0][1],
d = tri[2][1] - tri[0][1],
i = a * d - b * c;
/* Degenerate tri. */
if(i === 0.0)
return null;
var u = (d * (p[0] - tri[0][0]) - b * (p[1] - tri[0][1])) / i,
v = (a * (p[1] - tri[0][1]) - c * (p[0] - tri[0][0])) / i;
/* If we're outside the tri, fail. */
if(u < 0.0 || v < 0.0 || (u + v) > 1.0)
return null;
return [u, v];
}
};
if(typeof module !== "undefined")
module.exports = Delaunay;
})();