深度优先遍历（DFS)刷题记录

这几天 leetcode 坚持打卡 顺便刷刷题
leetcode DFS tag 简单题

判断一棵树是不是对称二叉数。

这道题看看是蛮简单的，想想也挺简单的。从根节点开始递归，判断左右子树是否相等，相等就是对称二叉树，但那仅限于root节点的下一层，你在递归遍历它左子树，很显然2的左节点是3，右节点是4 按照这个评判标准 它并不是对称二叉树。就很烦 想不出什么解题方法。。。

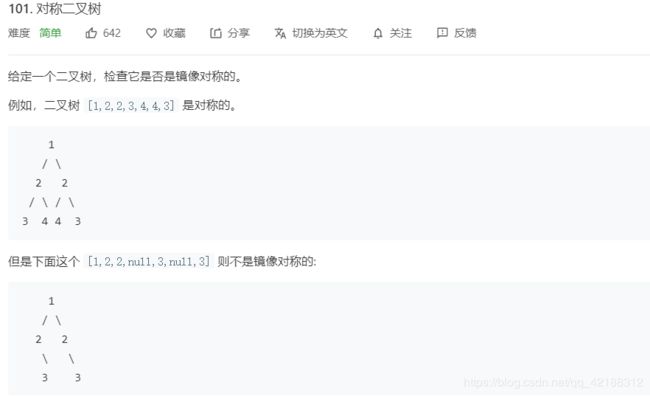
只好去看官方题解了

    bool isMirror(TreeNode* t1, TreeNode* t2) {
    if (t1 == NULL && t2 == NULL) return true;
    if (t1 == NULL || t2 == NULL) return false;
    return (t1->val == t2->val)
        && isMirror(t1->right, t2->left)
        && isMirror(t1->left, t2->right);
#两个树的根节点是否相等 及图中两个绿色的节点值受否相等
#一棵树照了镜子后 它的左子树应该是他的右子树 所以只要判断一棵树左子树是否和另一棵树的右子树相同就行了。这需要递归下去，如图就是分别比较蓝色部分，黄色部分。
    }

    bool isSymmetric(TreeNode* root) {
         return isMirror(root,root);
    }

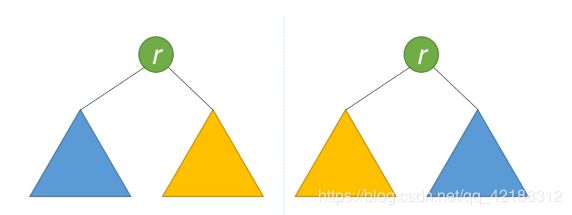
结合图，更容易理解。你不是对称二叉树吗 那你找个镜子，应该还是你自己吧。

解法二
运用队列，将要比较的两棵树的根节点保存起来，这个做法 我自己并没有实践过。
但我觉得 应该比递归要好理解一些，我说一下 我所理解的大致思路。

1. 首先将树的左右子树 放到队列中。
2. 只要队列不为空，就一直判断下去，如果如果一棵树的左孩子，右孩子。有一个孩子不在，那就不是对称的返回false,或者左孩子的值不等于右孩子，也直接返回。如果一路判断下来 都没问题 那就将接下来要比较的左右子树入队。
3. 关键 就关键在这个入队顺序了，将一个节点的左孩子和另一个节点的右孩子进行比较。

bool isSymmetric(TreeNode *root) {
    queue<TreeNode*> q;
    if(root == nullptr){
        return true;
    }
    q.push(root->left);
    q.push(root->right);

    while (!q.empty()){
        TreeNode* node1 = q.front();
        q.pop();
        TreeNode* node2 = q.front();
        q.pop();

        if(node1 == nullptr && node2 == nullptr){
            continue;
        }

        if(node1 == nullptr || node2 == nullptr){
            return false;
        }

        if(node1->val != node2->val){
            return false;
        }

        q.push(node1->left);
        q.push(node2->right);
        q.push(node1->right);
        q.push(node2->left);
    }

    return true;

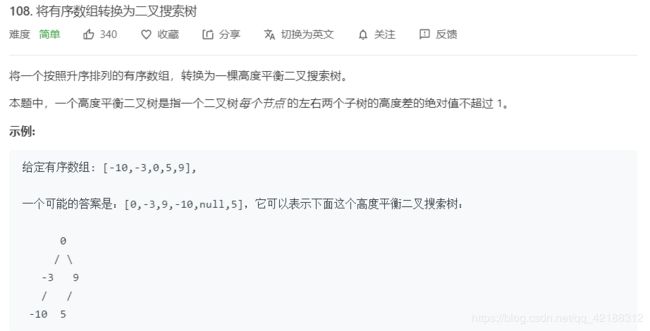
建立二叉搜索树。

选取中间节点作为根节点

    TreeNode* build(int left,int right,vector<int>& nums){
        if(left>right) return NULL;
        
        int mid=(left+right)/2;
        
        TreeNode* root=new TreeNode(nums[mid]);
        root->left=build(left,mid-1,nums);//建立左子树
        root->right=build(mid+1,right,nums);//建立右子树
        
        return root;
        
        
    }
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        if(nums.size()==0) return NULL;

        return build(0,nums.size()-1,nums);
    }

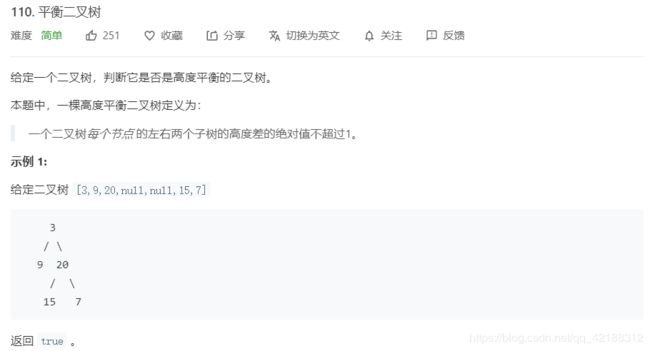
判断是否是平衡二叉树

思路
我怎么表示求出二叉树的深度呢 对没错 只要有孩子就递归下去，可边界是啥
没错 边界就是该节点为空 那我怎么表示一棵树的深度啊 毕竟左右子树高度不一样 没错就是max函数 只求最深的那棵树

    int getH(TreeNode* node){
        
        if(!node) return 0;
        int max_depth=max(getH(node->left),getH(node->right));
        
        return 1+max_depth;
        
        
    }
    bool isBalanced(TreeNode* root) {
        if(!root) return true;

        
        return abs(getH(root->left)-getH(root->right))<=1
            &&isBalanced(root->left)
            &&isBalanced(root->right);

    }

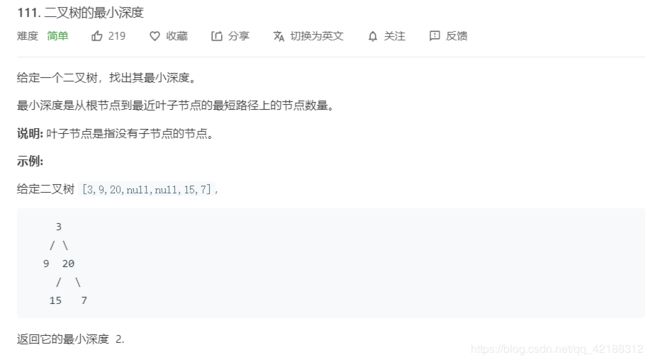
求二叉树的最小深度

这道题坑 确实挺多的 不是一般的多

  int minDepth(TreeNode* root) {
        if(!root) return 0;
        int min_left=minDepth(root->left);
        int min_right=minDepth(root->right);
        if(!root->left&&!root->right) return 1;
        else if(!root->left||!root->right) return max(min_left,min_right)+1;
        else
        return min(min_left,min_right)+1;
        
    }

求二叉树的直径

    int ans;
    int getH(TreeNode* root){
        if(!root) return 0;
        if(!root->left&&!root->right) return 1;
        int l=getH(root->left);//左子树最大节点数
        int r=getH(root->right);//右子树最大节点数
        ans=max(ans,l+r);
        return max(l,r)+1;
    }
  
    int diameterOfBinaryTree(TreeNode* root) {
        getH(root);
        return ans;
    
    }