CSAPP:datalab

试验获取请到官网 CSAPP

1.bitXor

int bitXor(int x, int y) {
  return (~(x&y)) & (~((~x)&(~y)));
}

• 左边表达式筛选出 0,1 1,0 0,0 三种情况得到1，右边表达式排除 0,0 得到1，二者一起得到 0,1 1,0 即异或
  
  

2.tmin

int tmin(void) {
  return 1<<31;
}

• 很简单

3.isTmax

int isTmax(int x) {
  return !(((~(x+1))^x) | (!(~x)));
}

• 或运算 | 左边筛选出 0x7fffffff 和 0xffffffff 得到全0 , 右边对于 0x7fffffff 得到全0， 对于 0xffffffff 得到1 ，经过或运算之后只有目标Tmax 0x7fffffff 会得到0，取非之后返回

4.AllOddBits

int allOddBits(int x) {
  int allodd0 = (0x55<<24) + (0x55<<16) + (0x55<<8) +0x55;
  return !(~(allodd0 | x));
}

• 比较简单，用奇数位全0，偶数位全1去进行或运算即可
  

5.negate

int negate(int x) {
  return (~x) + 1;
}

• x + ~x + 1 = 0
  

6.isAscciiDigit

int isAsciiDigit(int x) {
  int a = (x>>3)^0x6;
  int b = x^0x38;
  int c = x^0x39;
  return !a | !b | !c;
}

• a 筛选出 0x30 至 0x37 ，若符合 a 的值为 0 ，b 筛选 0x38 ， c 筛选 0x39

7.conditional

int conditional(int x, int y, int z) {
  int negative1 = ~1 + 1;	//-1
  int control = !x + negative1;		//x=0 ,c=0 ;x!=0 ,c=0xffffffff 
  return (y&control) + (z&(~control));
}

• 想了好久，思路在代码里，关键点是 0-1=0xffffffff

8.isLessOrEqual

int isLessOrEqual(int x, int y) {
  int negativex = ~x+1;
  int a = !((!(x>>31))|(y>>31));	//x<0 且 y>=0
  int b = (( !((x>>31)^(y>>31)) ) & (!((y+negativex)>>31) | !(x^(1<<31)))); 
  //			x,y异号			且 ( 	y-x>=0			或   x=0xffffffff )
  return a | b;
}

• 这道题就是用来说明 x<=y 不代表 x-y<=0 的，Tmin 和 Tmax 两个边界很要命 ，还有运算可能溢出。
  

9.logicalNeg

int logicalNeg(int x) {
  return ((x|(~x+1))>>31)+1;;
}

• 除了 0 和 Tmin 以外，所有数和其补码都是异号的，而 Tmin 的符号位为1，所以在和自己的补码逻辑或运算以后，只有 0 的符号位为 0 ，以此求解

10.howManyBits

int howManyBits(int x) {
 int shift1,shift2,shift4,shift8,shift16;
 int sum;
 int t=((!x)<<31)>>31;//x为0时，t（二进制）全为1，x不为0时，全为1
 int t2=((!~x)<<31)>>31;//当x为-1时，t2全为1，否则，全为0
 int op=x^((x>>31));//正数不变，负数取反
 shift16=(!!(op>>16))<<4;//如果高十六位全为0，则0左移4位，不全为0，则1左移4（表示op要右移2^4位）位
 op=op>>shift16;
 shift8=(!!(op>>8))<<3;
 op=op>>shift8;
 shift4=(!!(op>>4))<<2;
 op=op>>shift4;
 shift2=(!!(op>>2))<<1;
 op=op>>shift2;
 shift1=(!!(op>>1));
 op=op>>shift1;
 sum=2+shift16+shift8+shift4+shift2+shift1;
 return(t2&1)|((~t2)&((t&1)|((~t)&sum)));
}

• 略有点复杂，最后参考了这篇 ，这个二分法挺巧妙的

11.floatScale2

unsigned floatScale2(unsigned uf) {
  int e = (uf>>23) & 0xff;
  int rte = e+1;
  if(!e)//e=0
	return (uf&0xf0000000) + ((uf&0x7fffff)<<1);
  else if(!(e^0xff))
	return uf;
  else if(rte&(1<<8))
	return ((uf>>31)<<31) + (0xff<<23);
  else
    return (uf&(0x807fffff)) + (rte<<23);
}

• 规格化的浮点数乘2就是把阶码加一，非规格化和特殊值单独处理
  

12.floatFloat2Int

int floatFloat2Int(unsigned uf)
{
  int e = (uf >> 23) & 0xff;	//阶码
  int f = uf & 0x7fffff;		//尾码
  int tag = uf & 0x80000000;	//符号位
  if (e <= 126)		//小于0
    return 0;
  else if (e > 157)	//上溢
    return 0x80000000;
  else		//范围内
  {
    int s = e - 127;
    f = f + 0x800000;
    if (s >= 23)
    {
      int r = f << (s - 23);
      if (tag)
        return -r;
      else
        return r;
    }
    else
    {
      int r = (f >> (23 - s));
      if (tag)
        return -r;
      else
        return r;
    }
  }
}

• 题目不难，就是逻辑有点复杂，还要注意c/c++中的舍入是断尾法

13.floatPower2

unsigned floatPower2(int x) {
    unsigned INF = 0xff << 23; // 阶码全1
    int e = 127 + x;    // 得到阶码
    if (x < 0) // 阶数小于0直接返回0
        return 0;
    if (e >= 255) // 阶码>=255直接返回INF
        return INF;
    return e << 23;
    // 直接将阶码左移23位，尾数全0，规格化时尾数隐藏有1个1作为底数
}

• 不难

最后一题有个小插曲，就是最后一个题目测试时会提示死循环 .
但是逻辑是没有问题的，最后看了下测试文件的代码，在 btest.c 文件的开头限制了超时时间为10s，

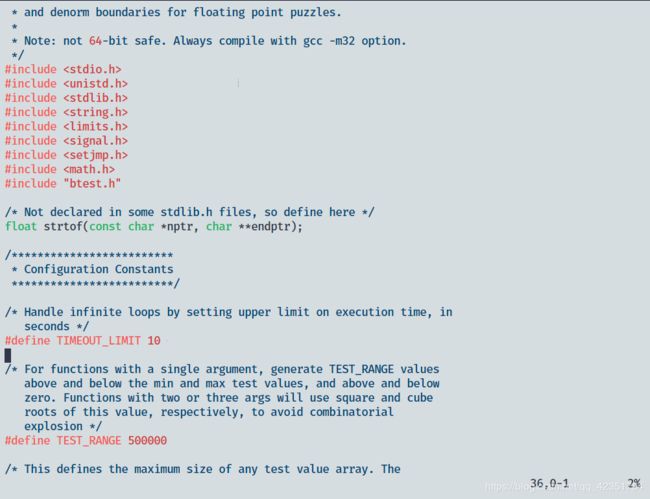
将TIMEOUT_LIMIT修改为100，测试通过

最后是完整文件

完整文件

小结

慕名而来看了CSAPP，不得不说看了这本书写的真的很好，看完第二章我对浮点数的认知确实更清晰了，后续我做了其他lab之后，也会逐一发上来，欢迎大家关注。

打个广告

博客原答地址，欢迎大家访问