软件构造实验六
- 实验目标概述
本次实验训练学生的并行编程的基本能力,特别是 Java 多线程编程的能力。 根据一个具体需求,开发两个版本的模拟器,仔细选择保证线程安全(threadsafe) 的构造策略并在代码中加以实现,通过实际数据模拟,测试程序是否是线程安全 的。另外,训练学生如何在 threadsafe 和性能之间寻求较优的折中,为此计算吞 吐率和公平性等性能指标,并做仿真实验。
⚫ Java 多线程编程
⚫ 面向线程安全的 ADT 设计策略选择、文档化
⚫ 模拟仿真实验与对比分析
- 实验环境配置
无需新配置环境
Window10
Jdk8
Eclipse
在这里给出你的GitHub Lab6仓库的URL地址(Lab6-学号)。
https://github.com/ComputerScienceHIT/Lab6-1170300527.git
- 实验过程
请仔细对照实验手册,针对三个问题中的每一项任务,在下面各节中记录你的实验过程、阐述你的设计思路和问题求解思路,可辅之以示意图或关键源代码加以说明(但千万不要把你的源代码全部粘贴过来!)。
本程序在main包下的Main类中开始执行,直接GUI可视化输出,故里面只有一个Gui的构造方法
多线程无法测试,只能在test中使用sleep函数使其也保持不中止,其他方法为大量的GUI,而且选择具有很大的随机性故测试很少
主要在每个的编写时使用main方法进行的测试,在最终结果中删除
-
- ADT设计方案
设计了哪些ADT、各自的作用、属性、方法;
给出每个ADT的specification;
(可选)以类图形式给出多个类之间的关系。
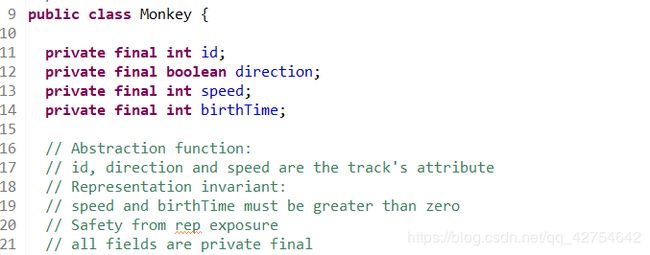
- Monkey:猴子
不可变数据类型,都由private final修饰
包含id,方向,速度,出生时间
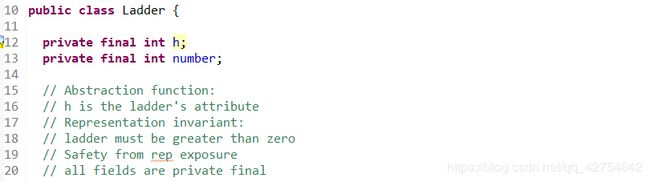
- Ladder:梯子
不可变数据类型,都由private final修饰
包含长度h,编号number
- LadderHaveMonkey梯子上的猴子
Ladder,该梯子,monkeys猴子为key,value为位置,locationMap与monkeys相反,currectDirection,当前梯子的方向
setCurrectDirection :设置当前梯子的方向
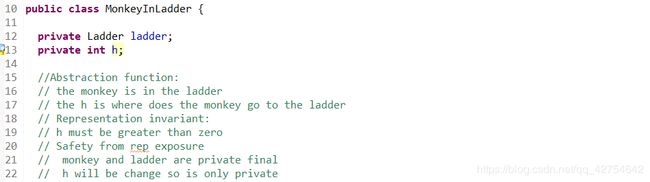
- MonkeyInLadder:猴子在梯子上的位置
可变数据类型,ladder为梯子,h为猴子所在梯子上的位置
使用时使用map和猴子绑定
-
- Monkey线程的run()的执行流程图
-
- 至少两种“梯子选择”策略的设计与实现方案
- 策略1
- 至少两种“梯子选择”策略的设计与实现方案
遍历ladder的set集合,拷贝一份以便于修改,寻找没有猴子的ladder,如果有,直接返回,如没有,寻找方向一致且当前方向第一个位置没有猴子的梯子注意两个方向上第一个位置不同一个为1一个是h。
-
-
- 策略2
-
首先没有猴子直接选,遍历ladder,找到其中猴子最少的梯子的集合,找到集合上最近的猴子,比较他们的速度找出最快的
-
-
- 策略3(可选)
-
选择最近猴子距离最远的梯子
优先找没猴子的,然后找同方向,对每个梯子上猴子位置排序,找到近的猴子的最远的梯子,同样要注意猴子的方向
-
- “猴子生成器”MonkeyGenerator
做成一个线程,包括时间,猴子总数,最大速度,间隔时间,通过循环产生猴子,每次sleep time秒,并把新生成的猴子加入的monkeys的集合中,get方法返回新生成的猴子,同时清空旧猴子集合
-
- 如何确保threadsafe?
首先里面所有关于猴子与梯子位置关系,状态,出生时间的数据都是共享的没有进行防御性拷贝,在不同线程,不同类,不同函数修改可以改变其他线程的状态
对选择梯子的函数加锁使用synchronized修饰,而且在选择梯子时对用到的位置关系的数据加锁,使下一个猴子选择时必须拿到锁才可以,由于上梯子不耗时,将选择梯子与上梯子放到一部操作
在梯子上行进时也加锁,防止选择到一个位置
多线程下map的keyset,valus不能直接转化很麻烦,改了n久哭了
遍历时各种报错加锁也不行,改变数据结构算法位置
-
- 系统吞吐率和公平性的度量方案
- 输出方案设计
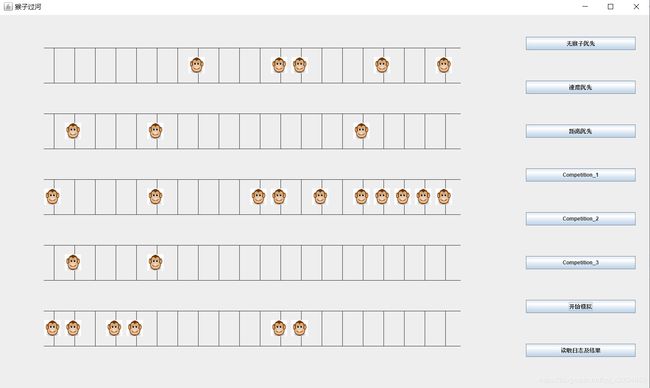
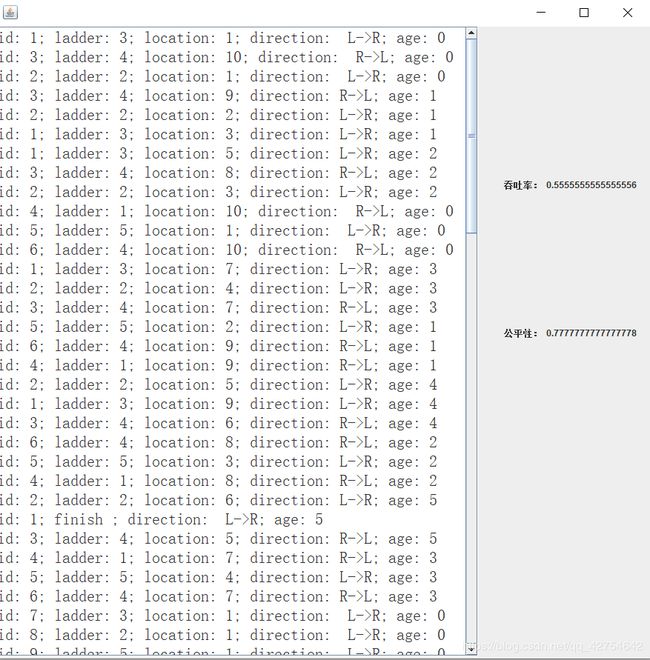
使用swing组件,实现了gui输入,可视化过河过程,
V1
V2
V3
日志效果相同
-
- 猴子过河模拟器v1
- 参数如何初始化
- 猴子过河模拟器v1
Gui页面上输入获取
-
-
- 使用Strategy模式为每只猴子选择决策策略
-
设计crossstrategy接口,三个策略分别继承这个接口
Ladderhavemonkey为梯子上猴子的位置,monkey为选择梯子的猴子
返回值为选择的梯子编号
-
- 猴子过河模拟器v2
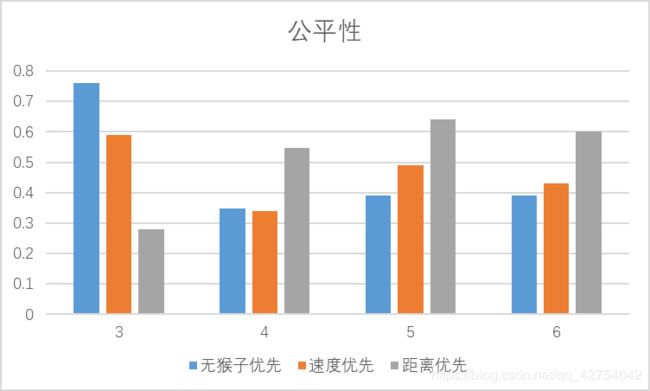
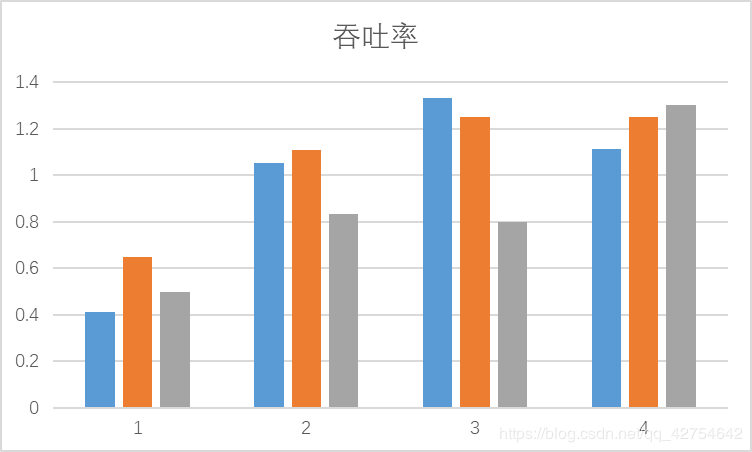
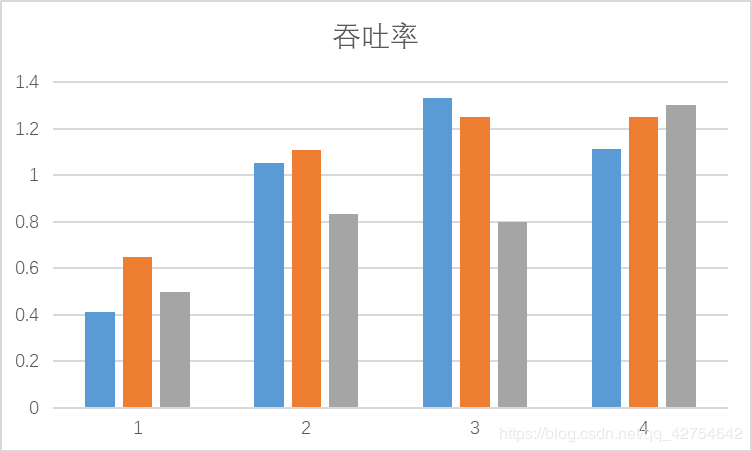
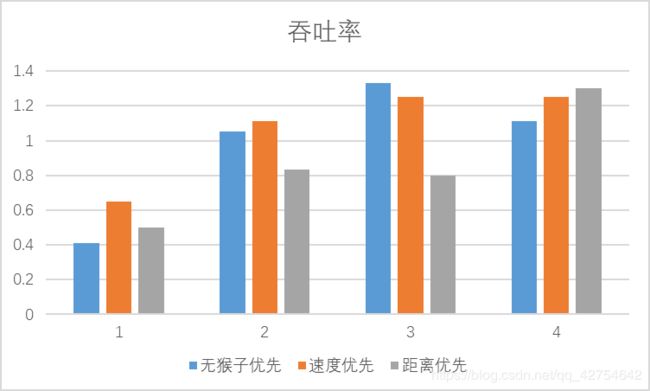
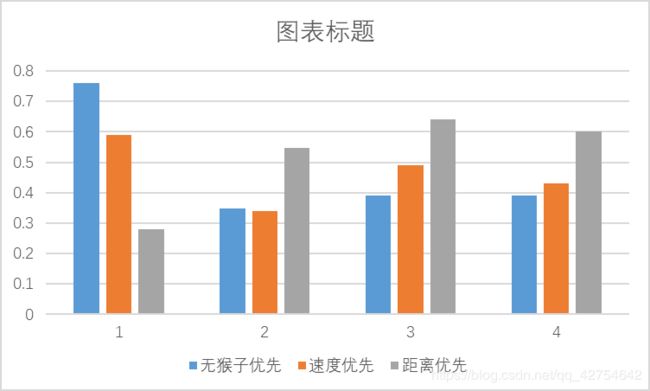
在不同参数设置和不同“梯子选择”模式下的“吞吐率”和“公平性”实验结果及其对比分析。
-
-
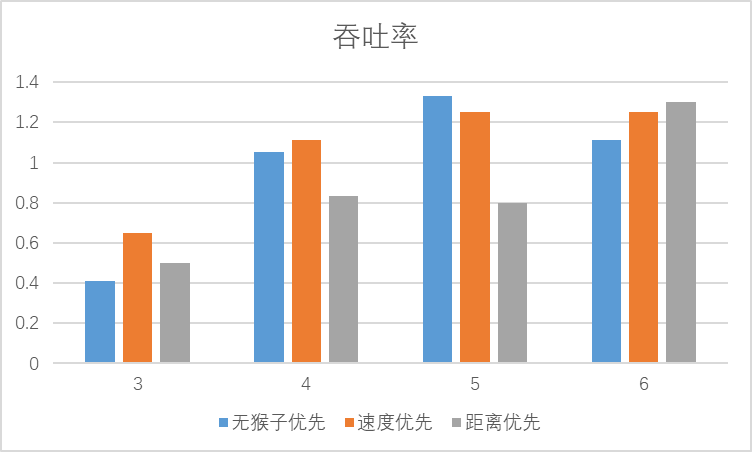
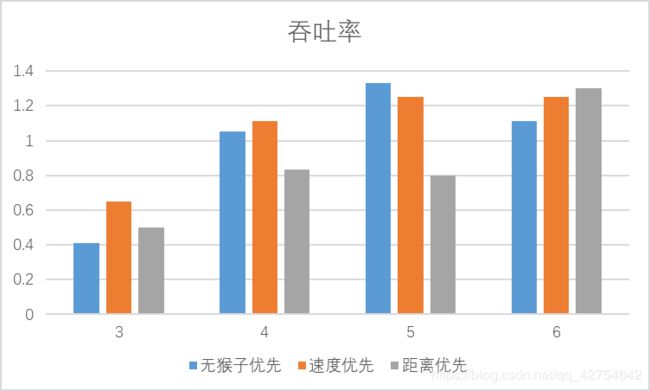
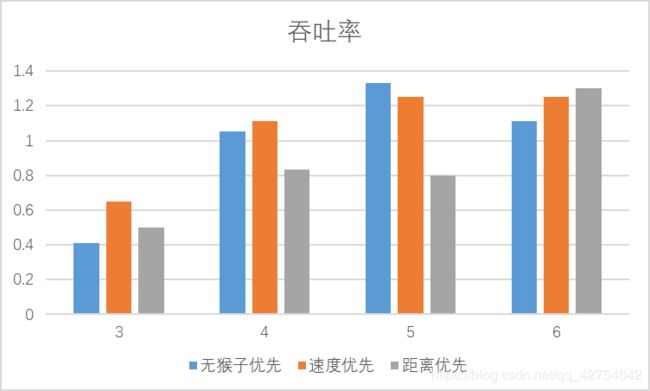
- 对比分析:固定其他参数,选择不同的决策策略
-
| 梯子数量 |
梯子长度 |
时间间隔 |
猴子数量 |
单次数量 |
最大速度 |
| 3,4,5,6 |
10 |
3 |
20 |
5 |
3 |
| 梯子数量 |
梯子长度 |
时间间隔 |
猴子数量 |
单次数量 |
最大速度 |
| 5 |
10 |
3,4,5,6 |
20 |
5 |
3 |
| 梯子数量 |
梯子长度 |
时间间隔 |
猴子数量 |
单次数量 |
最大速度 |
| 5 |
10 |
3 |
20,30,40,50 |
5 |
3 |
| 梯子数量 |
梯子长度 |
时间间隔 |
猴子数量 |
单次数量 |
最大速度 |
| 5 |
10 |
3 |
20 |
3,4,5,6 |
3 |
| 梯子数量 |
梯子长度 |
时间间隔 |
猴子数量 |
单次数量 |
最大速度 |
| 5 |
10 |
3 |
20 |
5 |
3,4,5,6, |
-
-
- 对比分析:变化某个参数,固定其他参数
-
上一问中已经对其进行了完备的测试,不同策略下的相同参数,相同参数下的不同策略在同一表格下进行了对比,结果更加直观,这里就不再赘述了
-
-
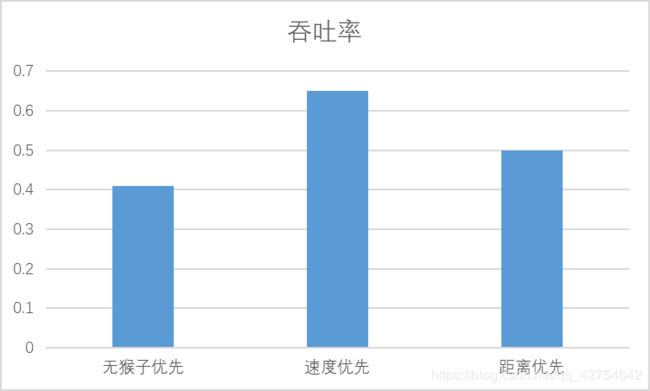
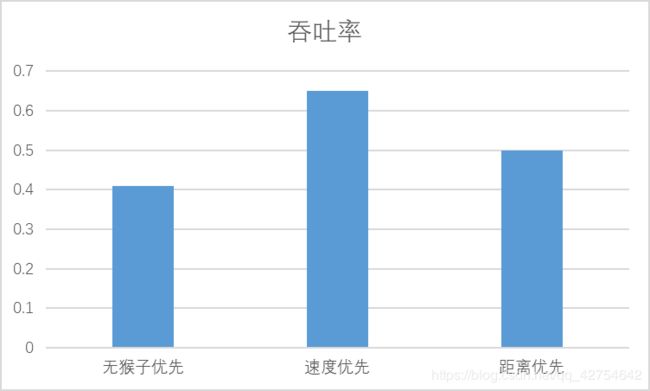
- 分析:吞吐率是否与各参数/决策策略有相关性?
-
有关,梯子增多速度会随之提升,速度增快也会提升速度,当单次生成的猴子过多时,会有大量的猴子在等待,因此也就不会与生成猴子的间隔时间有太大关系
决策不同速度不同,选择梯子不同,前进的速度也会有区别
梯子越长吞吐率越大与公平性关系不大
产生猴子的时间间隔越长,吞吐率下降同时公平性下降
猴子数量越多,吞吐率越高,
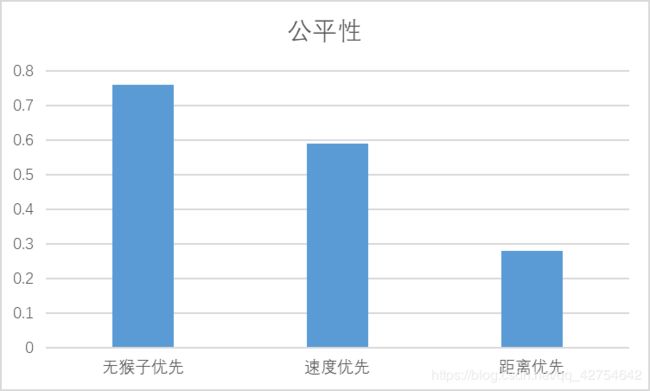
当生成速度和时间梯子数目一样时公平性较高,同一时间的都可以上梯子,而过多时就会有等待和下次的竞争
-
-
- 压力测试结果与分析
-
1.猴子特别多梯子不足
| 梯子数量 |
梯子长度 |
时间间隔 |
猴子数量 |
单次数量 |
最大速度 |
| 5 |
10 |
3 |
200 |
5 |
5 |
| 梯子数量 |
梯子长度 |
时间间隔 |
猴子数量 |
单次数量 |
最大速度 |
| 5 |
40 |
3 |
200 |
5 |
20 |
压力测试中吞吐率较正常测试低很多,虽然速度快了很多,但由于存在速度较小的在前面阻塞速度提升并不是很大
-
- 猴子过河模拟器v3
针对教师提供的三个文本文件,分别进行多次模拟,记录模拟结果。
|
|
吞吐率 |
公平性 |
| Competiton_1.txt |
|
|
| 第1次模拟 |
2.238 |
0.352 |
| 第2次模拟 |
2.307 |
0.334 |
| 第3次模拟 |
2.381 |
0.379 |
| 第4次模拟 |
2.542 |
0.390 |
| 第5次模拟 |
2.220 |
0.452 |
| 第6次模拟 |
2.236 |
0.325 |
| 第7次模拟 |
2.345 |
0.364 |
| 第8次模拟 |
2.109 |
0.362 |
| 第9次模拟 |
2.879 |
0.328 |
| 第10次模拟 |
2.645 |
0.369 |
| 平均值 |
2.3902 |
0.3655 |
| Competiton_2.txt |
|
|
| 第1次模拟 |
4.717 |
0.6245 |
| 第2次模拟 |
4.982 |
0.741 |
| 第3次模拟 |
4.689 |
0.698 |
| 第4次模拟 |
4.353 |
0.562 |
| 第5次模拟 |
4.185 |
0.658 |
| 第6次模拟 |
5.182 |
0.696 |
| 第7次模拟 |
4.652 |
0.687 |
| 第8次模拟 |
4.365 |
0.874 |
| 第9次模拟 |
4.239 |
0.454 |
| 第10次模拟 |
4.754 |
0.634 |
| 平均值 |
4.6118 |
0.66285 |
| Competiton_3.txt |
|
|
| 第1次模拟 |
1.1111 |
0.2166 |
| 第2次模拟 |
1.25 |
0.625 |
| 第3次模拟 |
1.298 |
0.073 |
| 第4次模拟 |
1.024 |
0.203 |
| 第5次模拟 |
1.036 |
0.264 |
| 第6次模拟 |
0.985 |
0.197 |
| 第7次模拟 |
0.964 |
0.165 |
| 第8次模拟 |
1.105 |
0.217 |
| 第9次模拟 |
1.006 |
0.264 |
| 第10次模拟 |
0.904 |
0.193 |
| 平均值 |
1.04581 |
0.24176 |