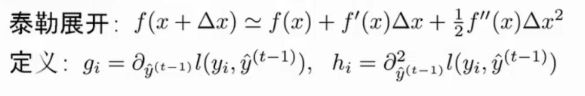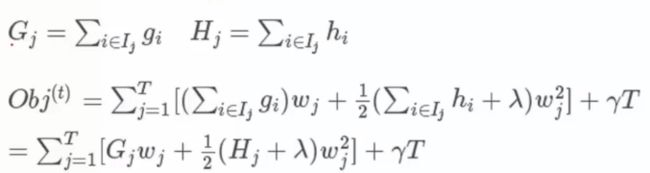集成学习之XGBoost算法推导总结
一、从GBDT到XGBoost
作为GBDT的高效实现,XGBoost是一个上限特别高的算法,因此在算法竞赛中比较受欢迎。简单来说,对比原算法GBDT,XGBoost主要从下面三个方面做了优化:
一是算法本身的优化:在算法的弱学习器模型选择上,对比GBDT只支持决策树,还可以直接很多其他的弱学习器。在算法的损失函数上,除了本身的损失,还加上了正则化部分。在算法的优化方式上,GBDT的损失函数只对误差部分做负梯度(一阶泰勒)展开,而XGBoost损失函数对误差部分做二阶泰勒展开,更加准确。算法本身的优化是我们后面讨论的重点。
二是算法运行效率的优化:对每个弱学习器,比如决策树建立的过程做并行选择,找到合适的子树分裂特征和特征值。在并行选择之前,先对所有的特征的值进行排序分组,方便前面说的并行选择。对分组的特征,选择合适的分组大小,使用CPU缓存进行读取加速。将各个分组保存到多个硬盘以提高IO速度。
三是算法健壮性的优化:对于缺失值的特征,通过枚举所有缺失值在当前节点是进入左子树还是右子树来决定缺失值的处理方式。算法本身加入了L1和L2正则化项,可以防止过拟合,泛化能力更强。
在上面三方面的优化中,第一部分算法本身的优化是重点也是难点。现在我们就来看看算法本身的优化内容。
二、XGBoost树的定义
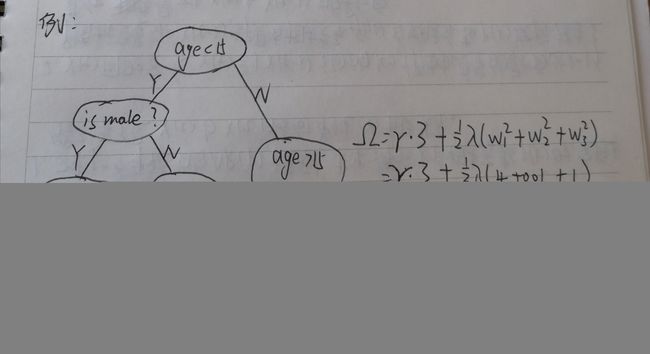
举个例子,我们要预测一家人谁是谁,则可以先通过年龄区分开小孩和大人,然后再通过性别区分开是男是女,如下图所示。
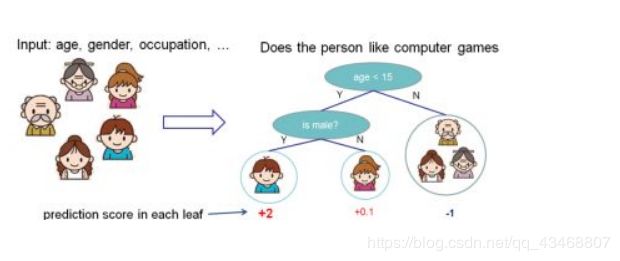
就这样,训练出了2棵树tree1和tree2,类似之前gbdt的原理,两棵树的结论累加起来便是最终的结论,所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加:2 + 0.9 = 2.9。爷爷的预测分数同理:-1 + (-0.9)= -1.9。具体如下图所示
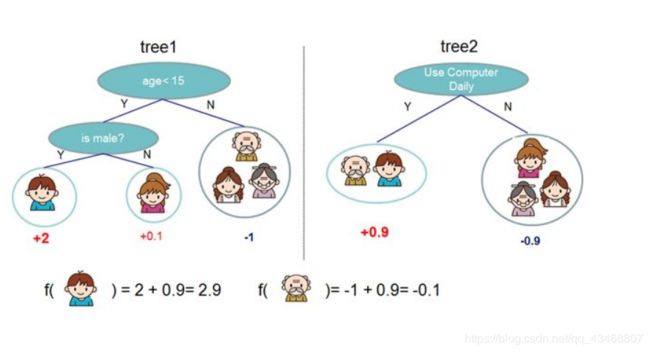
这看起来跟 GBDT 很相似,事实上如果不考虑工程实现、解决问题上的一些差异,xgboost与gbdt比较大的不同就是目标函数的定义。
三、Xgboost公式推导
3.1、先定义以下几个函数:
- 预测函数
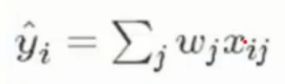
w w w为权重, x x x 为样本,即叶子节点值 - 目标函数
目标函数有很多表示方法,此处使用均方误差
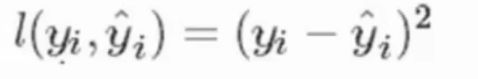
- 如何最优函数解?
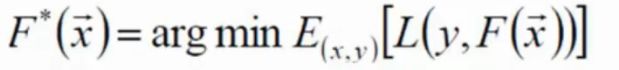
表示计算所有样本的损失,再除以样本个数求平均值,即等价于计算样本的期望,求出最小的期望。 - 集成算法表示
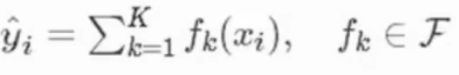
3.2、Xgboost解决问题思路
通过每加一棵树来提升整体的准确性,公式如下
y ^ i ( 0 ) = 0 没 有 树 \hat{y}_i^{(0)}=0~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~没有树 y^i(0)=0 没有树
y i ( 1 ) = f 1 ( x i ) = y ^ i ( 0 ) + f 1 ( x i ) 一 棵 树 y_i^{(1)}=f_1(x_i)=\hat{y}_i^{(0)}+f_1(x_i)~~~~~~~~~~~~~~~~~~~~~一棵树 yi(1)=f1(xi)=y^i(0)+f1(xi) 一棵树
y i ( 2 ) = f 1 ( x i ) + f 2 ( x i ) = y i ( 1 ) + f 2 ( x i ) 两 棵 树 y_i^{(2)}=f_1(x_i)+f_2(x_i)=y_i^{(1)}+f_2(x_i)~~~~~~~两棵树 yi(2)=f1(xi)+f2(xi)=yi(1)+f2(xi) 两棵树
y i ( t ) = ∑ k = 1 t f k ( x i ) = y i ( t − 1 ) + f t ( x i ) 所 有 棵 树 y_i^{(t)}=\sum_{k=1}^{t}f_k(x_i)=y_i^{(t-1)}+f_t(x_i)~~~~~~~~所有棵树 yi(t)=k=1∑tfk(xi)=yi(t−1)+ft(xi) 所有棵树
上式中参数解释:
- y i ( t ) y_i^{(t)} yi(t) 表示第 t t t 轮的模型预测
- y i ( t − 1 ) y_i^{(t-1)} yi(t−1) 表示前 t − 1 t-1 t−1 轮模型预测
- f t ( x i ) f_t(x_i) ft(xi) 表示加入的新决策树
当树的叶子节点数目越大,过拟合的风险也就越高,因此定义XGBoost 惩罚项为:
Ω ( h t ) = γ T + λ 2 ∑ j = 1 T w j 2 Ω(ht)=γT+\frac{λ}{2}\sum_{j=1}^Tw^2_{j} Ω(ht)=γT+2λj=1∑Twj2
- T T T : 叶子结点的个数
- γ γ γ : 惩罚力度
- w j 2 w^2_{j} wj2 : 权重 w w w 进行 l 2 l_2 l2 惩罚,即模平方
此时,为了选择出每轮需要加入的树,可以用一个 f f f 函数来让我们目标函数的损失最大的降低,即
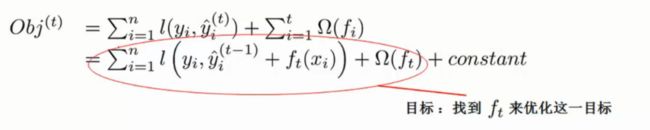
O b j ( t ) = ∑ i = 1 n l ( y i , y ^ i ( t ) ) + ∑ i = 1 t Ω f ( i ) Obj^{(t)}=\sum_{i=1}^{n}l(y_i,\hat y_i^{(t)})+\sum_{i=1}^{t}Ωf(i)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ Obj(t)=i=1∑nl(yi,y^i(t))+i=1∑tΩf(i)
= ∑ i = 1 n l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) + Ω ( f t ) + c o n s t a n t =\sum_{i=1}^{n}l\left(y_i,\hat y_i^{(t-1)}+f_t(x_i)\right)+Ω(f_t)+constant =i=1∑nl(yi,y^i(t−1)+ft(xi))+Ω(ft)+constant
上式中的 c o n s t a n t constant constant 表示常数,我们现在的目标是找到 f t f_t ft 来使得目标函数 O b j ( t ) Obj^{(t)} Obj(t) 的值最小。
- x x x 等价于 y i , y ^ i ( t − 1 ) y_i,\hat y_i^{(t-1)} yi,y^i(t−1),即表示原来的模型
- Δ x \Delta x Δx 等价于 f t ( x i ) f_t(x_i) ft(xi),即表示新加入到模型
- g i g_i gi 即 f ′ ( x ) f^{\prime}(x) f′(x),是目标函数的一阶导数
- h i h_i hi 是目标函数的二阶导数
将目标函数转换得:
![]()
因为每加入一棵树,之前的树就被当做一个整体,即一个固定值,可将其看作常数,与后面的 c o n s t a n t constant constant 结合成新的常数项。因为常数项对结果的影响很小,所以先不考虑它,对上式化简得:
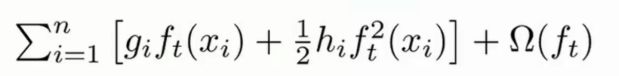
f t ( x i ) f_t(x_i) ft(xi) 表示加入新的树,也就是样本到达每个新的叶子节点。 f t ( x i ) f_t(x_i) ft(xi) 等价于 w ⋅ x i w\cdot x_i w⋅xi,即叶子节点中的 “权重” 乘以 “样本值”,对上式化简得:
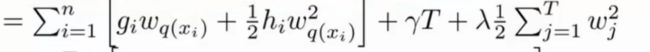
上式一直表示对样本遍历,而这种遍历方式比较复杂,因此我们可以从叶子节点开始遍历,对每个叶子节点分别求一阶导数 g i g_i gi 和二阶导数 h i h_i hi, 这样相比更为简单,上式化简得:
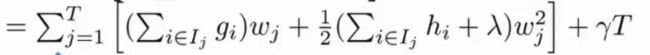
- I j I_j Ij为指示函数,表示包含某些样本的集合
现在我们需要求出什么样的 w j w_j wj 能使得目标函数值最小,因此对目标函数求关于 w j w_j wj 的导数,并让其等于0,公式如下
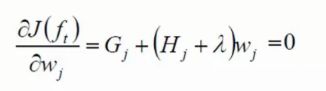
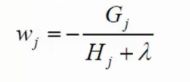
将求得的 w j w_j wj 带入目标函数得
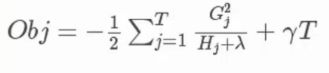
现在我们已经将最终的目标函数推导出来了,在我们使用 X g b o o s t Xgboost Xgboost 时只需计算出它的得分值 G a i n Gain Gain来判别就可以了
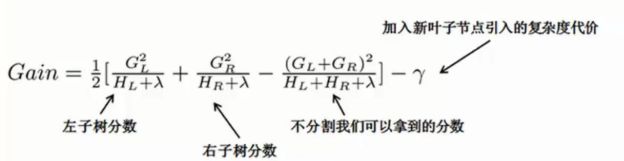
得分值 G a i n Gain Gain 的推导如下
不 分 割 = − 1 2 ( G L + G R ) 2 H L + H R + λ 不分割=-\frac{1}{2}\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 不分割=−21HL+HR+λ(GL+GR)2
分 割 后 : 左 子 树 = − 1 2 G L 2 H L + λ 分割后:左子树=-\frac{1}{2}\frac{G_L^2}{H_L+\lambda}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 分割后:左子树=−21HL+λGL2
右 子 树 = − 1 2 G R 2 H R + λ 右子树=-\frac{1}{2}\frac{G_R^2}{H_R+\lambda}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 右子树=−21HR+λGR2
G a i n = 不 分 割 − 分 割 Gain=不分割 - 分割~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ Gain=不分割−分割
= − 1 2 ( G L + G R ) 2 H L + H R + λ − ( − 1 2 G L 2 H L + λ ) − ( − 1 2 G R 2 H R + λ ) − λ =-\frac{1}{2}\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}-(-\frac{1}{2}\frac{G_L^2}{H_L+\lambda})-(-\frac{1}{2}\frac{G_R^2}{H_R+\lambda})-\lambda =−21HL+HR+λ(GL+GR)2−(−21HL+λGL2)−(−21HR+λGR2)−λ
= − 1 2 ( G L + G R ) 2 H L + H R + λ + 1 2 ( G L 2 H L + λ + G R 2 H R + λ ) − λ =-\frac{1}{2}\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}+\frac{1}{2}(\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda})-\lambda~~~~~~~~~~~~ =−21HL+HR+λ(GL+GR)2+21(HL+λGL2+HR+λGR2)−λ
= 1 2 ( − ( G L + G R ) 2 H L + H R + λ + G L 2 H L + λ + G R 2 H R + λ ) − λ =\frac{1}{2}(-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}+\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda})-\lambda~~~~~~~~~~~~~~~ =21(−HL+HR+λ(GL+GR)2+HL+λGL2+HR+λGR2)−λ
= 1 2 ( G L 2 H L + λ + G R 2 H R + λ − ( G L + G R ) 2 H L + H R + λ ) − λ =\frac{1}{2}(\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda})-\lambda~~~~~~~~~~~~~~~~~ =21(HL+λGL2+HR+λGR2−HL+HR+λ(GL+GR)2)−λ
四、XGBoost算法主流程
这里我们总结下XGBoost的算法主流程,基于决策树弱分类器。
输入是训练集样本 I = ( x , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) I={(x,y_1),(x_2,y_2),...,(x_m,y_m)} I=(x,y1),(x2,y2),...,(xm,ym), 最大迭代次数 T T T, 损失函数L, 正则化系数 λ , γ λ,γ λ,γ,输出是强学习器 f ( x ) f(x) f(x)
对迭代轮数t=1,2,…T有:
- 计算第i个样本 ( i − 1 , 2 , . . m ) (i-1,2,..m) (i−1,2,..m) 在当前轮损失函数L基于 f t − 1 ( x i ) f_t−1(x_i) ft−1(xi) 的一阶导数 g t i g_{ti} gti,二阶导数 h t i h_{ti} hti ,计算所有样本的一阶导数和 G t = ∑ i = 1 m g t i G_t=\sum_{i=1}^{m}g_{ti} Gt=∑i=1mgti,二阶导数和 H t = ∑ i = 1 m h t i H_t=\sum_{i=1}^mh_{ti} Ht=∑i=1mhti 。
- 基于当前节点尝试分裂决策树,默认分数score=0,G和H为当前需要分裂的节点的一阶二阶导数之和。
对特征序号 k=1,2…K:
2.1 G L = 0 , H L = 0 G_L=0,H_L=0 GL=0,HL=0
2.2 将样本按特征k从小到大排列,依次取出第i个样本,依次计算当前样本放入左子树后,左右子树一阶和二阶导数和:
2.3 尝试更新最大的分数:
s c o r e = m a x ( G a i n , 1 2 ( G L 2 H L + λ + G R 2 H R + λ − ( G L + G R ) 2 H L + H R + λ ) − λ ) score=max(Gain,\frac{1}{2}(\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda})-\lambda) score=max(Gain,21(HL+λGL2+HR+λGR2−HL+HR+λ(GL+GR)2)−λ) - 基于最大score对应的划分特征和特征值分裂子树。
- 如果最大 s c o r e score score 为 0,则当前决策树建立完毕,计算所有叶子区域的 w t j w_{tj} wtj, 得到弱学习器 h t ( x ) h_t(x) ht(x),更新强学习器 f t ( x ) f_t(x) ft(x),进入下一轮弱学习器迭代。如果最大 %score$ 不是 0,则转到第 2 步继续尝试分裂决策树。
以上为 X g b o o s t Xgboost Xgboost 的总结。
参考资料
https://blog.csdn.net/hellozhxy/article/details/82143554