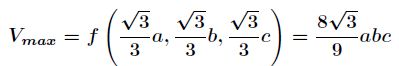拉格朗日乘子法(简单易懂的说明)
拉格朗日乘子法(Lagrange Multiplier)
之前在高中就有一直听到拉格朗日,拉格朗日是一个很牛逼哄哄的大佬。在学习SVM的时候,居然也见到了他的身影。让我们了解一下拉格朗日乘子法的具体内容。
在学习过程中,有时会遇到一些最优化问题。这里提到的最优化问题通常是指对于给定的某一函数,求其在指定作用域上的全局最小值(无论最大最小值都可以转化为最小值),二者均是求解最优化问题的方法不同之处在于应用的情形不同。
一般情况下,最优化问题会碰到下面三种:
- 无约束条件
- 等式约束条件
- 不等式约束条件
什么是拉格朗日乘子法?
基本的拉格朗日乘子法就是求函数 f ( x 1 , x 2 , . . . ) f(x_1,x_2,...) f(x1,x2,...)在约束条件 g ( x 1 , x 2 , . . . ) g(x_1,x_2,...) g(x1,x2,...)=0下的极值的方法。其主要思想是将约束条件函数与原函数联立,从而求出使原函数取得极值的各个变量的解。拉格朗日乘子法是在支持向量机为了更好的求解间距的方法。
在求解最优问题中,拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush Kuhn Tucker)条件是两种最常用的方法,在有等式约束时使用拉格朗日乘子法,在有不等式约束的时候使用KTT条件。
1. 无约束条件
例子:
m i n f ( x ) minf(x) minf(x)
这是最简单的情况,解决方法是函数对变量求导,令求导函数等于0的点可能是极值点。将结果带回原函数进行验证。
2. 等式约束条件
设目标函数为f(x),约束条件为hk(x),形如:s.t. 表示subject to ,“受限于”的意思,l表示有l个约束条件。
m i n f ( x ) minf(x) minf(x)
s . t . h k ( x ) = 0 k = 1 , 2 , . . . , l s.t. h_k(x)=0 k=1,2,...,l s.t.hk(x)=0k=1,2,...,l
则解决方法是消元法或者拉格朗日法。这里主要讲拉格朗日法,后面提到的KKT条件是对拉格朗日乘子法的一种泛化
例如给定椭球:
x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 \frac{x^2}{a^2} + \frac{y^2}{b^2}+\frac{z^2}{c^2} = 1 a2x2+b2y2+c2z2=1
求这个椭球的内接长方体的最大体积。
我们将这个转化为条件极值问题,即在条件
x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 \frac{x^2}{a^2} + \frac{y^2}{b^2}+\frac{z^2}{c^2} = 1 a2x2+b2y2+c2z2=1下,求 f ( x , y , z ) = 8 x y z f(x,y,z)=8xyz f(x,y,z)=8xyz的最大值。
当然这个问题实际可以先根据条件消去 z (消元法),然后带入转化为无条件极值问题来处理。但是有时候这样做很困难,甚至是做不到的,这时候就需要用拉格朗日乘数法了。 首先定义拉格朗日函数F(x):
F ( x , λ ) = f ( x ) + ∑ k − 1 l λ k h k ( x ) F(x, \lambda) = f(x) + \sum_{k-1}^l\lambda_kh_k(x) F(x,λ)=f(x)+k−1∑lλkhk(x)(其中 λ k \lambda k λk是各个约束条件的待定系数。)
然后解变量的偏导方程:
∂ F ∂ x i = 0... ∂ F ∂ λ k \frac{\partial F}{\partial x_i} = 0...\frac{\partial F}{\partial \lambda_k} ∂xi∂F=0...∂λk∂F
如果有l个约束条件,就应该有l+1个方程。求出的方程组的解就可能是最优化值(高等数学中提到的极值),将结果带回原方程验证就可得到解。
回到上面的题目,通过拉格朗日乘数法将问题转化为:
F ( x , y , z , λ ) = f ( x , y , z ) + λ ψ ( x , y , z ) = 8 x y z + λ ( x 2 a 2 + y 2 b 2 + z 2 c 2 − 1 ) F(x, y, z, \lambda) = f(x,y,z) + \lambda \psi(x,y,z)=8xyz + \lambda(\frac{x^2}{a^2} + \frac{y^2}{b^2}+\frac{z^2}{c^2}-1) F(x,y,z,λ)=f(x,y,z)+λψ(x,y,z)=8xyz+λ(a2x2+b2y2+c2z2−1)
对 F ( x , y , z , λ ) F(x,y,z,\lambda) F(x,y,z,λ)求偏导得:
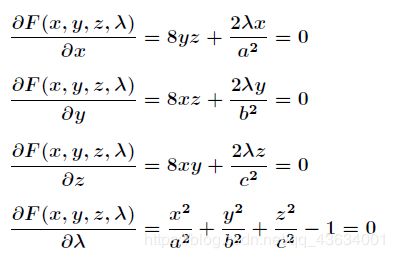
联立前面三个方程得到 b x = a y bx=ay bx=ay 和 a z = c x az=cx az=cx,带入第四个方程解之
3. 不等式约束条件
设目标函数f(x),不等式约束为g(x),有的教程还会添加上等式约束条件h(x)。此时的约束优化问题描述如下:
m i n f ( x ) minf(x) minf(x)
s . t . h j ( X ) = 0 j = 1 , 2 , . . . , p s.t. h_j(X)=0 j=1,2,...,p s.t.hj(X)=0j=1,2,...,p
g k ( X ) ≤ 0 k = 1 , 2 , . . . , q g_k(X) \leq 0 k=1,2,...,q gk(X)≤0k=1,2,...,q
则我们定义不等式约束下的拉格朗日函数L,则L表达式为:
L ( X , λ , μ ) = f ( X ) + ∑ j = 1 p λ j h j ( X ) + ∑ k = 1 p μ k g k ( X ) L(X,\lambda, \mu) = f(X)+\sum^p_{j=1}\lambda_jh_j(X)+\sum^p_{k=1}\mu_kg_k(X) L(X,λ,μ)=f(X)+j=1∑pλjhj(X)+k=1∑pμkgk(X)
其中f(x)是原目标函数,hj(x)是第j个等式约束条件,λj是对应的约束系数,gk是不等式约束,uk是对应的约束系数。
常用的方法是KKT条件,同样地,把所有的不等式约束、等式约束和目标函数全部写为一个式子L(a, b, x)= f(x) + ag(x)+bh(x)
KKT条件是说最优值必须满足以下条件:
- L(a, b, x)对x求导为零;
- h(x) =0;
- a*g(x) = 0;
求取这些等式之后就能得到候选最优值
该方法适用于约束条件下求极值的问题。对于没有约束的极值问题,显然,如果某一点是极值的必要条件是该点的各方向的偏导数皆为零,也就是说,如果偏导数不全为零,那么就不可能是极值。