第六章计算机的运算方法
文章目录
- 6.1无符号数和有符号数
- 一、无符号数
- 二、有符号数
- 1.机器数与真值
- 2.原码表示法
- 3.补码表示法
- 4.反码表示法
- 5.移码表示法
- 6.2 数的定点表示和浮点表示
- 定点表示
- 浮点表示
- 6.3 定点运算
- 一、移位运算
- 二、加减法运算
- 溢出判断
- 三、乘法运算
- 原码一位乘法
- 补码一位乘法
- 四、 除法运算
- 原码除法
- 补码除法
- 6.4 浮点四则运算
- 一、浮点加减运算
- 二、浮点乘除运算
- 6.5 算数逻辑单元
- 一、ALU电路
- 二、快速进位链
6.1无符号数和有符号数
一、无符号数
二、有符号数
1.机器数与真值
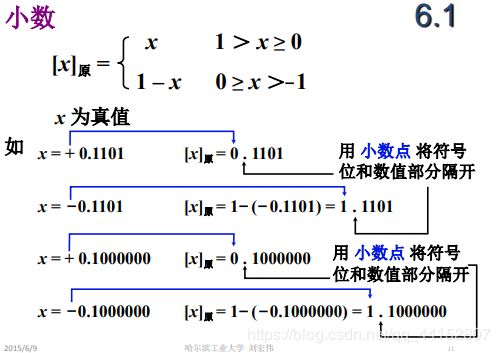
2.原码表示法
3.补码表示法
- 1011用8421法看出为11,模为24即为16。16-11=5即8421法得0101。故:-1011=+0101(mod 24)
- 也可用二进制减法做,24为10000,10000-1011=+0101

为了多个符号位,之前的计算用的24与现在符号位需要的24;2个24相加为25,故用25作为模


- 此时小数是mod 2,若是mod 4则小数的前面是2位.mod 8则小数的前面是3位。mod 16则小数的前面是3位


真值为负时,补码转到原码符号位不变,每位取反,末位加1


70=64+4+2即是1000110
负数的补码更好算的方法:符号位不变,X1的非,X2的非到XK的非,后面的10000等照写,得到的就是这个负数的补码
-1有补码无原码。
4.反码表示法
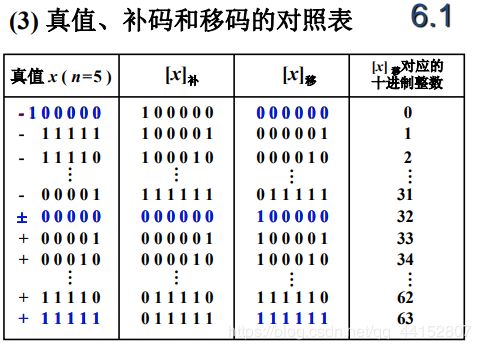
5.移码表示法

31用32-1表示即25-1即100000-1为11111

 补码换到移码符号位取反即可
补码换到移码符号位取反即可

6.2 数的定点表示和浮点表示
定点表示
浮点表示


尾数的绝对值<=1,阶码是整数。
r=2:尾数当中每一位二进制数表示了尾数中的一位2进制数。
r=4:尾数当中的两位二进制数表示一位4进制的尾数
r=8:尾数中的三位二进制数表示一位8进制的尾数
r=16:4位二进制数表示一位16进制数
当r=2 N=11.0101——>=0.110101×210因为右移两位数据,数据本身大小变为原来的1/4,则阶码部分变为10,10是二进制表示即十进制中的2即22即就是4
N=0.00110101×2100小数点往左移了四位,变为原来的1/16,阶码中而二进制中的100就是4.即24=16
二进制:-11,-10,-1,0,1,10,11




r=2——>左规:数据向左移动;右规:数据向右移动,数据值变为原来的1/2


19=16+2+1即10011
19/128即将10011除128,128=27即10011数据相对于小数点右移7位;每移一位相当于除以2。变为0.0010011
浮点机当中用分号将阶码和尾数隔开



6.3 定点运算
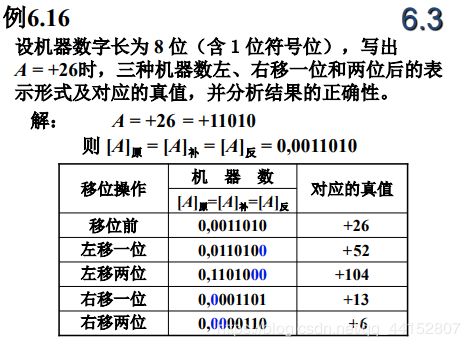
一、移位运算

对于计算机来说,都是数据移动而小数点的位置不变
左移一位,机器数的真值变为原来的2倍;右移变为原来的1/2倍,有时可能因为低位丢掉影响了精度

左移最高位会被丢掉,最低位补;
右移最低位丢掉,符号位的下一位高位补
即空出的地方补
左移一位,真值变为原来的2倍
对于正数,三种机器数移位后符号位均不变,左移时最高位丢1,结果出错;右移时最低位丢1,影响精度。
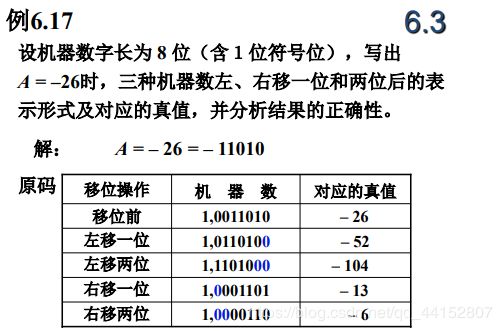
负数原码左移时,高位丢1,结果出错,右移时,低位丢1,影响精度
负数的补码左移时,高位丢0(原码的1),结果出错;右移时,低位丢1,影响精度

第一行第四个:左移——>负数的反码最低位添1,最高位丢掉,符号位不变
第二行第四个:右移——>负数的反码最高位添1,最低位丢掉

算数移位符号位不参与移位运算,逻辑移位全部参与移位运算
可以用带进位的移位将丢掉的最高位记录在进位中
二、加减法运算
- 对整数来说mod 2n+1不管是正数还是负数它(A)的补码形式都可以用X+2n+1表示(不用区分加数或被加数的正负,直接A的补码表示为2n+1+A)
- 对小数来说,A的补码可以直接变为2+A
- 对于补码,连同符号位一起运算,和的符号通过计算过程自动产生,
符号位产生的进位自动丢掉
由[A+B]补求A+B——>直接将[A+B]补取反末位加1
== -B的补码=将B的补码数值位每位取反,末位加1==
练习一:在小数定点机中计算结果为大于1的数发生溢出
练习二:整数定点机中机器字长为8位计算结果-138超出了这种机器所能表示的范围(-128~127),发生上溢
溢出判断

当两位符号位不同,表示溢出。不论是否发生溢出,高位符号位表示真正的符号。
双符号位的模可以变为2n+2

GA,GS标记做加法、减法。
在整数定点机中,机器数采用补码,双符号位,若它的十六进制表示为C0H,则它的真值为(-64)。
三、乘法运算
原码一位乘法

移位次数控制乘法操作的结束
乘数最后一位为1,部分积+X,右移一位
乘数最后一位为0,部分积+0,右移一位
最后符号位异或
补码一位乘法
- 第三列为附加位,开始的时候此位=0.
- 比较第三列和第二列最后一位(0-1=-1),则需要加上[-x]补再右移(因为是补码则算数右移),此时补码是负数右移补1。等等依次类推步骤
- 第二行第一列,蓝色的1是由于此时补码是负数右移补1
- 第三行第一列,蓝色的0是由于此时补码是正数右移补0
- 到第五行,0-1=-1则加上[-x]补。
得到结果,此时不用再移位——>最后一步不移位。
[X.Y]中Y为负数,加上[-x]补;Y是正数则不用
符号位参与运算,得到的也是补码形式
被乘数x取双符号参与运算,部分积初值为0。
乘数y取单符号位,乘数y末位增加一个附加位0.
判断y的最后两位:
- 倒数第一位-倒数第二位=0——>直接右移一位
- 倒数第一位-倒数第二位>0——>加x补后右移
- 倒数第一位-倒数第二位<0——>加-x补后右移
- 最后一位不右移
四、 除法运算
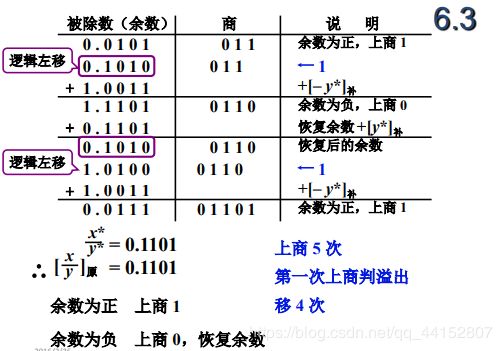
原码除法

若不满足约定,即,小数定点运算中被除数的绝对值>除数的绝对值,(即第一步发现上商为1)——>发生溢出
整数定点除法中被除数的绝对值>除数的绝对值,则发生了溢出

余数>0,上商为1,余数左移一位并加上[y*]补除数
余数<0,上商为0,余数左移一位并加上[-y*]补除数
最后符号位异或
补码除法
余数[Ri]补与[y]补同号——>上商为1,新余数左移一位+[-y]补
余数[Ri]补与[y]补异号——>上商为0,新余数左移一位+[y]补
最后一步,左移一位,末位商恒置1
6.4 浮点四则运算
浮点运算的特点:阶码(指数)运算和尾数(基值)运算分开进行
一、浮点加减运算
- 阶码对齐则可以进行加减运算
- 求阶差用补码形式实现
- 阶码减小一位,尾数就要左移一位保证数据不发生变化
- 而计算机中x向y看齐,尾数左移有可能使1被移掉,引发错误,故
尾数左移并不合适 - 若y向x看齐,最右侧数据位丢失,只会影响精度而不影响大小
- 小阶向大阶看齐

- 这道题中阶码四位,阶符占了两位;尾数六位,尾符占了两位。
- 阶码在前;尾数在后(2位阶符,2位阶码;2位尾符
.4位尾数) - jx补-jy补=jx补+[-jy补]
- [-jy补]=原码取反加1
- 对阶后就可以尾数求和,但此时得到的是不规格化的数

- 规格化是为了尽可能的提高在计算机中浮点数的表示精度
- 若尾数的基值r=4,则 1 4 ≤ ∣ S ∣ < 1 \frac{1}{4} \leq|S|<1 41≤∣S∣<1
- S表示尾数
- 原码无论正负,第一位数总为1
- 补码,符号位和第一数位不同


- 尾数的绝对值大于1,尾数溢出要右规
- 两个正数相加就可能会造成01.XXXXX这种形式的溢出
- 恒置1法,不管末位丢掉什么数据,计算结果的最低有效位均为1
- 如果采用0舍1入法进行舍入处理,则0.01010110011舍去最后一位后,结果为(0.0101011010)。
- 整个浮点数发生的溢出,阶码比+127还大就发生了上溢;
- 阶码比-128还小就是下溢。下溢作为0看,上溢进入出错处理
- 在浮点数中,当数的绝对值太小,以至于小于能表示的数据时,称为浮点数的下溢
二、浮点乘除运算
- 阶码相加减(乘积阶码为[jx]补+[jy]补;商的阶码为[jx]补-[jy]补)
- 尾数相乘或除;被除尾数的绝对值一定小于除数尾数的绝对值
若被除数尾数绝对值大于除数尾数绝对值,则被除数进行调整——>被除数尾数右移,阶码+1,直到|被除数尾数|<|除数尾数| - 结果向左规格化并舍入处理
- 判断溢出:尾数不可能发生溢出,运算结果可能发生溢出
6.5 算数逻辑单元
一、ALU电路
- Ai、Bi表示参加运算的数据,Fi为输出。
- Ki决定是什么类型的运算
- 输入、输出端都要连接寄存器,保存运算结果
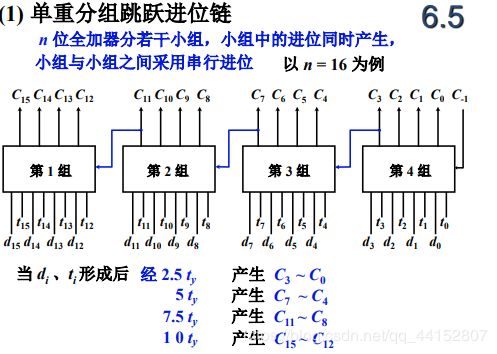
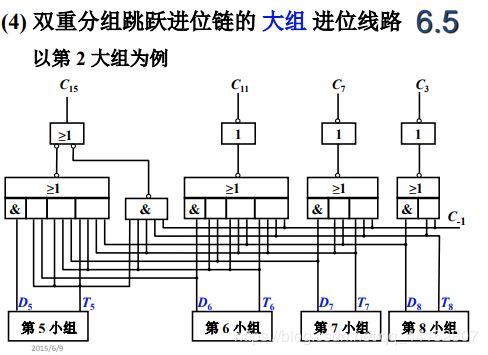
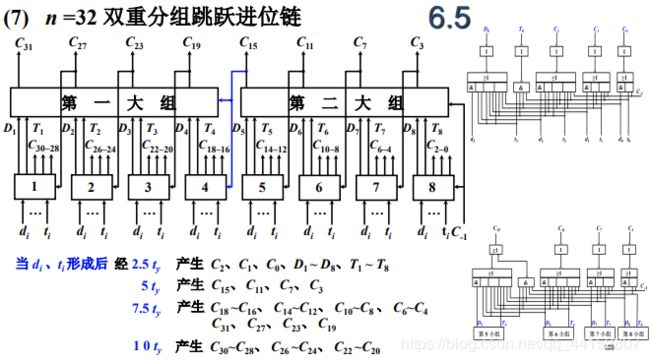
- 影响加法器运算速度的就是进位链