五天学会Pytorch
文章目录
- 我的Pytorch学习笔记
- 前言:
- Day 1 数据的基本操作 Tensor的使用
- Tensor的基础使用
- **Tensor重点知识**:
- 自动求梯度 Autograd
- 概念
- 例子 Tensor
- Day 2&3 深度学习基础
- 线性回归(适用于连续值等预测问题)
- 1.生成数据集
- 2. 读取数据
- 3. 定义模型
- 4.初始化模型参数
- 5.定义Loss Function
- 6定义优化算法
- 7.训练模型
- 神经网络图
- Softmax回归(用于离散值分类问题)
- Softmax回归模型
- 交叉熵损失函数
- 多层感知机
- 隐藏层 **Hidden layer**
- 激活函数
- 多层感知机的介绍
- 数据导入
- 定义模型
- 读取小批量数据
- 训练模型
- 模型选择\欠拟合\过拟合
- 训练误差(traing error)&泛化误差(generalization error)
- 模型的选择
- 欠拟合和过拟合
- 应用**丢弃法**应对过拟合问题
- 正向传播、反向传播和计算图
- 正向传播
- 反向传播 **TODO:没有细看**
- 个人思考及疑问
- 知识点及总结
- Day 4 深入深度学习
- 模型构造
- 继承`Module`类来构造模型
- `Module`的子类
- 模型的参数访问\初始化\共享
- 参数访问
- Day 4&5 卷积神经网络 convolutional neural network
- LeNet模型实现
- 模型建立
- 获取数据
- 训练模型
- AlexNet模型实现
- 模型建立
- ※Print 模型与测试模型
- 读取数据集
- 训练模型
- VGG模型实现
- VGG块
- VGG网络
- ※Print 模型与测试模型
- 读取数据与训练模型
- Day 5 循环神经网络
- 循环神经网络
- 周杰伦专辑歌词读取
- 读取数据集
- 建立字符索引
- 时序数据的采样
- 循环神经网络实现
- 读取数据集
- 模型建立
- 定义一个预测函数
- TODO 梯度裁剪
- 训练模型
- GRU门控循环单元
- 重置门和更新门
- 隐藏状态
- 读取数据集
- 建立模型&训练模型
- LSTM 长短期记忆
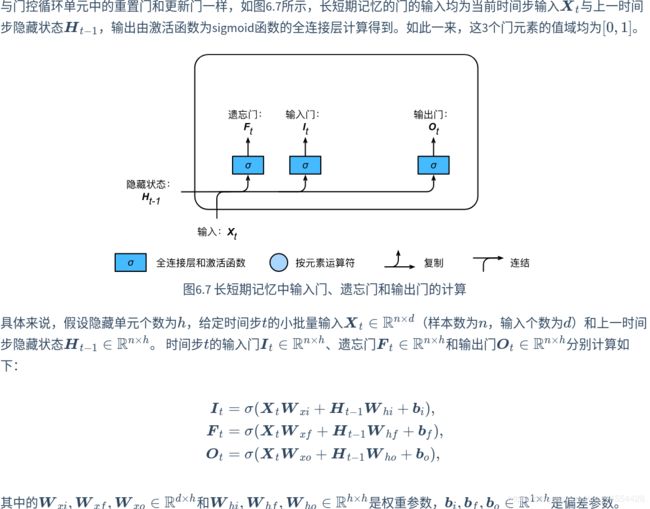
- INPUT GATE\FORGET GATE\OUTPUT GATE
- 候选记忆细胞
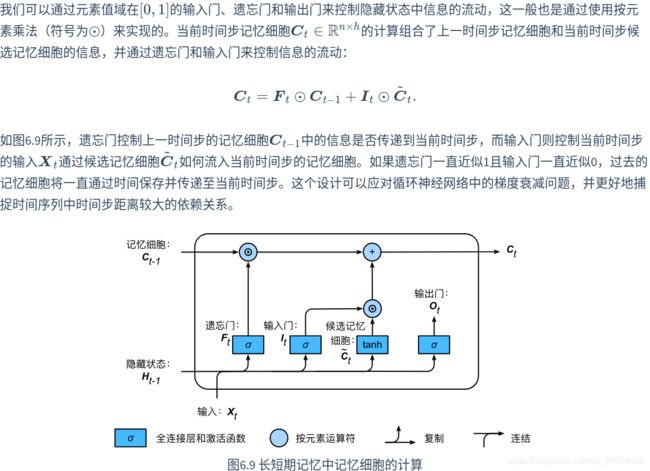
- 记忆细胞
- 隐藏状态
- 读取数据集
- 模型简洁实现
- Pytorch小结
我的Pytorch学习笔记
联系邮箱:[email protected]
前言:
- 所有的学习资料来自以下参考文档:
参考文档 - 该笔记是在jupyter notebook上完成,导出为md文件可能阅读不是很舒服,如果有朋友需要.ipynb或.py文件,可以发邮件私聊我
- 该笔记是动态笔记,仍在不断更新,如果你有好的建议或意见,也可以私我邮箱
import torch
import torch.nn as nn
import numpy as np
import use_package
import qiqi_package as qiqi
import torch.utils.data as Data
import sys
import torchvision
import torchvision.transforms as transforms
import time
import math
importing Jupyter notebook from qiqi_package.ipynb
Day 1 数据的基本操作 Tensor的使用
Tensor的基础使用
- 创建Tensor,先创建一个空的Tensor
- 未初始化的Tensor的创建
- 随机初始化的Tensor创建
- 全零的Tensor的创建
x = torch.empty(5, 3)
print(x)
x = torch.rand(5, 3)
print(x)
x = torch.zeros(5, 3, dtype=torch.long) #类型选择为long
print(x)
- Tensor的一些基本用法
- 获取Tensor的尺寸
- 加法
Note:跳过一部分过于基础的学习,直接进入重点部分
Tensor重点知识:
- 索引 :我们可以使用类似NumPy的索引操作来访问Tensor的一部分,需要注意的是:索引出来的结果与原数据共享内存,也即修改一个,另一个会跟着修改。
- 运算内存 :索引操作不会修改我们的内存,而像y=x+y则会修改内存,我们可以用python自带的id函数来确定内存地址是否相同.
- Tensor 和 Numpy的互换
∗ ∗ 注 意 ∗ ∗ \color{#FF3030}{**注意**} ∗∗注意∗∗ a+=1 和 a=a+1是不一样的 a+=1不会改变内存及a的位置不变,对应到Tensor中就是 Tensor a 和 Numpy b均加1,
而a=a+1则a的内存地址改变,只加a,b的值不再改变 - Tensor on Gpu
#运算内存
x = torch.tensor([1, 2])
y = torch.tensor([3, 4])
id_before = id(y)
y = y + x
id_now =id(y)
print('y原来的id',id_before,'\ny之后的id',id_now)
print('可以看出两者id不一样',id(y) == id_before) # False
# Tensor 和 Numpy互换 Tensor->Numpy
a = torch.ones(5)
b = a.numpy()
print('ida:',id(a),'idb:',id(b))
print(a, b)
a+=1 #attention!
print('a:',a)
print('b:',b)
a=a+1 #attention!
print('a:',a)
print('b:',b)
# Tensor 和 Numpy互换 Numpy->Tensor
a = np.ones(5)
b = torch.from_numpy(a)
print(a, b)
a += 1
print(a, b)
a = a+ 1 #attention
print(a, b)
#Tensor on Gpu
# 以下代码只有在PyTorch GPU版本上才会执行
if torch.cuda.is_available():
device = torch.device("cuda") # GPU
y = torch.ones_like(x, device=device) # 直接创建一个在GPU上的Tensor
x = x.to(device) # 等价于 .to("cuda")
z = x + y
print(z)
print(z.to("cpu", torch.double)) # to()还可以同时更改数据类型
自动求梯度 Autograd
概念
-
上一节介绍的Tensor是这个包的核心类,如果将其属性
.requires_grad设置为True,它将开始追踪(track)在其上的所有操作(这样就可以利用链式法则进行梯度传播了)。完成计算后,可以调用.backward()来完成所有梯度计算。此Tensor的梯度将累积到.grad属性中。 -
注意在
y.backward()时,如果y是标量,则不需要为backward()传入任何参数;否则,需要传入一个与y同形的Tensor。 -
如果不想要被继续追踪,可以调用
.detach()将其从追踪记录中分离出来,这样就可以防止将来的计算被追踪,这样梯度就传不过去了。此外,还可以用with torch.no_grad()将不想被追踪的操作代码块包裹起来,这种方法在评估模型的时候很常用,因为在评估模型时,我们并不需要计算可训练参数(requires_grad=True)的梯度。 -
Function是另外一个很重要的类。Tensor和Function互相结合就可以构建一个记录有整个计算过程的有向无环图(DAG)。每个Tensor都有一个.grad_fn属性,该属性即创建该Tensor的Function, 就是说该Tensor是不是通过某些运算得到的,若是,则grad_fn返回一个与这些运算相关的对象,否则是None。
例子 Tensor
1. 创建一个`Tensor`,并设置`requires_grad=True`,并观察其梯度
2. 进行运算操作
x = torch.ones(2,2,requires_grad=True)
print(x)
print(x.grad_fn,'可以看到此时暂无grad')
y = x+ 2
print(y)
print(y.grad_fn)
注意x是直接创建的,所以它没有grad_fn, 而y是通过一个加法操作创建的,所以它有一个为grad_fn。
像x这种直接创建的称为叶子节点,叶子节点对应的grad_fn是None。
判断x,y是否叶子节点
print(x.is_leaf, y.is_leaf) # True False
z = y * y * 3
out = z.mean()
print('Z:',z, '\nOUT:',out)
Note:这里没有详细往下写,参考连接
https://tangshusen.me/Dive-into-DL-PyTorch/#/chapter02_prerequisite/2.3_autograd
之后用到再写
x = torch.ones(1,requires_grad=True)
print(x.data) # 还是一个tensor
print(x.data.requires_grad) # 但是已经是独立于计算图之外
y = 2 * x
x.data *= 100 # 只改变了值,不会记录在计算图,所以不会影响梯度传播
y.backward()
print(x) # 更改data的值也会影响tensor的值
print(x.grad)
Day 2&3 深度学习基础
线性回归(适用于连续值等预测问题)
其输出是一个连续值,适用于预测等回归问题.
import torch
from IPython import display
from matplotlib import pyplot as plt
import random
1.生成数据集
sample num=1000;
featuer num =2
w=[2,-3.4]T ;b=4.2
以及一个e 随机噪声项 来生成label ;e服从 mean=0,std=0.01的正态分布
num_inputs = 2
num_example = 1000
true_w = [2,-3.4]
true_b = 4.2
features = torch.randn(num_example,num_inputs,dtype = torch.float32)
#1000 raw ; 2 column
labels = true_w[0]*features[:,0]+true_w[1]*features[:,1]+true_b
labels += torch.tensor(np.random.normal(0,0.01,size = labels.size()),dtype = torch.float32)
qiqi.set_figsize((3.5,2.5))
plt.scatter(features[:,1].numpy(),labels.numpy(),1)#散点图
2. 读取数据
利用Pytorch.utils中的data函数
batch_size = 10
#将featuers 和 labels组合
dataset=Data.TensorDataset(features,labels)
data_iter =Data.DataLoader(dataset,batch_size,shuffle=True)
for X, y in data_iter:
print('Features:',X, '\nLabels:',y)
3. 定义模型
利用torch.nn模块
nn的核心数据结构是Module,它是一个抽象概念,既可以表示神经网络中的某个层(layer),也可以表示一个包含很多层的神经网络。在实际使用中,最常见的做法是继承nn.Module,撰写自己的网络/层。一个nn.Module实例应该包含一些层以及返回输出的前向传播(forward)方法。下面先来看看如何用nn.Module实现一个线性回归模型。
class LinearNET(nn.Module):
def __init__(self,n_feature):
super(LinearNET, self).__init__()
self.linear = nn.Sequential(
nn.Linear(n_feature,1)
)
# forward 定义前向传播
def forward(self,x):
y = self.linear(x)
return y
net = LinearNET(num_inputs)
print(net)
nn.Sequential的简便定义方法:
我个人最常用的方法是写法1
'''
# 写法一
net = nn.Sequential(
nn.Linear(num_inputs, 1)
# 此处还可以传入其他层
)
# 写法二
net = nn.Sequential()
net.add_module('linear', nn.Linear(num_inputs, 1))
# net.add_module ......
# 写法三
from collections import OrderedDict
net = nn.Sequential(OrderedDict([
('linear', nn.Linear(num_inputs, 1))
# ......
]))
print(net)
print(net[0])
'''
可以通过net.parameters() 来查看模型所有的可学习参数,此函数将返回一个生成器。
print('包含features和labels')
for param in net.parameters():
print(param)
4.初始化模型参数
在使用net前,我们需要初始化模型参数,如线性回归模型中的权重和偏差。PyTorch在init模块中提供了多种参数初始化方法。这里的init是initializer的缩写形式。我们通过init.normal_将权重参数每个元素初始化为随机采样于均值为0、标准差为0.01的正态分布。偏差会初始化为零。
nn.init.normal_(net.linear[0].weight,mean=0,std=0.01)
nn.init.constant_(net.linear[0].bias,val=0)
5.定义Loss Function
PyTorch在nn模块中提供了各种损失函数,这些损失函数可看作是一种特殊的层,PyTorch也将这些损失函数实现为nn.Module的子类。我们现在使用它提供的均方误差损失作为模型的损失函数。
loss = nn.MSELoss()
6定义优化算法
同样,我们也无须自己实现小批量随机梯度下降算法。torch.optim模块提供了很多常用的优化算法比如SGD、Adam和RMSProp等。下面我们创建一个用于优化net所有参数的优化器实例,并指定学习率为0.03的小批量随机梯度下降(SGD)为优化算法。
optimizer =torch.optim.SGD(net.parameters(),lr=0.03)
print(optimizer)
有时候我们不想让学习率固定成一个常数,那如何调整学习率呢?主要有两种做法。一种是修改optimizer.param_groups中对应的学习率,另一种是更简单也是较为推荐的做法——新建优化器,由于optimizer十分轻量级,构建开销很小,故而可以构建新的optimizer。但是后者对于使用动量的优化器(如Adam),会丢失动量等状态信息,可能会造成损失函数的收敛出现震荡等情况。
7.训练模型
在使用Gluon训练模型时,我们通过调用optim实例的step函数来迭代模型参数。按照小批量随机梯度下降的定义,我们在step函数中指明批量大小,从而对批量中样本梯度求平均。
= 3
for epoch in range(1,+1):
for X,y in data_iter:
output = net(X)
l = loss(output,y.view(-1,1))
optimizer.zero_grad() # 梯度清零,等价于net.zero_grad()
l.backward()
optimizer.step()
print('epoch %d, loss: %f' % (epoch, l.item()))
下面我们分别比较学到的模型参数和真实的模型参数。我们从net获得需要的层,并访问其权重(weight)和偏差(bias)。学到的参数和真实的参数很接近。
dense = net.linear[0]
print(true_w,'\n',dense.weight)
print(true_b,'\n',dense.bias)
神经网络图
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XXWbk86F-1583034220052)(attachment:image.png)]
这是一个单层神经网络图(输入层不进行计算,故不被计入)
如图,当输出o和输入层中所有的神经元都连接时,这里的输出层又叫做
(fully-connected layer)or(dense layer)全连接层或稠密层
Softmax回归(用于离散值分类问题)
和线性回归不同,softmax回归的输出单元从一个变成了多个,且引入了softmax运算使输出更适合离散值的预测和训练。
Softmax回归模型
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DQ8csVYX-1583034220052)(attachment:image.png)]
- 其输出有多个,当每个输出都依赖所有的输入时,就是一个fully connected或dense layer
- 且softmax将所有输出的求和=1,及进行了概率化分布,每个输出的值*100%就是预测其的概率
交叉熵损失函数
简要来讲,就是只关心正确类别的预测概率,只要其值足够大,就能确保分类结果正确,而对不是其正确标签的其它值的概率一概不看
当一个样本有多个标签时,同理
多层感知机
我们已经介绍了包括线性回归和softmax回归在内的单层神经网络。然而深度学习主要关注多层模型。在本节中,我们将以多层感知机**(multilayer perceptron,MLP)**为例,介绍多层神经网络的概念。
隐藏层 Hidden layer
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SRrM42Az-1583034220053)(attachment:image.png)]
输入层不计入计算,则有两层,且隐藏层和输出层都是fully connected
激活函数
不再赘述
多层感知机的介绍
多层感知机就是含有至少一个隐藏层的由全连接层组成的神经网络,且每个隐藏层的输出通过激活函数进行变换。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。以单隐藏层为例并沿用本节之前定义的符号,多层感知机按以下方式计算输出:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EJr3D9MV-1583034220054)(attachment:2020-02-19%2010-45-02%20%E7%9A%84%E5%B1%8F%E5%B9%95%E6%88%AA%E5%9B%BE.png)]
其中ϕ表示激活函数。
数据导入
下面的mnist_train和mnist_test都是torch.utils.data.Dataset的子类,所以我们可以用len()来获取该数据集的大小,还可以用下标来获取具体的一个样本。训练集中和测试集中的每个类别的图像数分别为6,000和1,000。因为有10个类别,所以训练集和测试集的样本数分别为60,000和10,000。
mnist_train = torchvision.datasets.FashionMNIST(root='./Datasets/FashionMNIST', train=True, download=True, transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='./Datasets/FashionMNIST', train=False, download=True, transform=transforms.ToTensor())
print(type(mnist_train))
print(len(mnist_train),len(mnist_test))
#来访问一个样本:
feature,label = mnist_train[0]
print(feature.shape,label)
# 数值标签转为文本标签
def get_fashion_mnist_labels(labels):
text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
return [text_labels[int(i)] for i in labels]
def show_fashion_mnist(images, labels):
"""可以在一行内画出多个图"""
qiqi.use_svg_display()
# 这里的_表示我们忽略(不使用)的变量
_, figs = plt.subplots(1, len(images), figsize=(12, 12))
for f, img, lbl in zip(figs, images, labels):
f.imshow(img.view((28, 28)).numpy())
f.set_title(lbl)
f.axes.get_xaxis().set_visible(False)
f.axes.get_yaxis().set_visible(False)
plt.show()
X, y = [], []
for i in range(10):
X.append(mnist_train[i][0])
y.append(mnist_train[i][1])
show_fashion_mnist(X, get_fashion_mnist_labels(y))
- 需要注意的是,feature的尺寸是 (C x H x W) 的,而不是 (H x W x C)。第一维是通道数,因为数据集中是灰度图像,所以通道数为1。后面两维分别是图像的高和宽。
- Fashion-MNIST中一共包括了10个类别,分别为t-shirt(T恤)、trouser(裤子)、pullover(套衫)、dress(连衣裙)、coat(外套)、sandal(凉鞋)、shirt(衬衫)、sneaker(运动鞋)、bag(包)和ankle boot(短靴)。以下函数可以将数值标签转成相应的文本标签。
定义模型
- 和softmax回归唯一的不同在于,我们多加了一个全连接层作为隐藏层。它的隐藏单元个数为256,并使用ReLU函数作为激活函数。
- 回归的输出层是一个全连接层,所以我们用一个线性模块就可以了。因为前面我们数据返回的每个batch样本x的形状为(batch_size, 1, 28, 28), 所以我们要先用view()将x的形状转换成(batch_size, 784)才送入全连接层。
num_inputs=784 #28*28 图片像素尺寸
num_outputs=10
num_hiddens=256
class LinearNet(nn.Module):
def __init__(self, num_inputs, num_hiddens,num_outputs):
super(LinearNet, self).__init__()
self.linear = nn.Sequential(
nn.Linear(num_inputs, num_hiddens),
nn.ReLU(),
nn.Linear(num_hiddens,num_outputs)
)
def forward(self, x): # x shape: (batch, 1, 28, 28)
y = self.linear(x.view(x.shape[0], -1))
return y
net = LinearNet(num_inputs,num_hiddens,num_outputs)
print(net)
#初始化参数
for params in net.parameters():
nn.init.normal_(params, mean=0, std=0.01)
读取小批量数据
我们将在训练数据集上训练模型,并将训练好的模型在测试数据集上评价模型的表现。前面说过,mnist_train是torch.utils.data.Dataset的子类,所以我们可以将其传入torch.utils.data.DataLoader来创建一个读取小批量数据样本的DataLoader实例。
在实践中,数据读取经常是训练的性能瓶颈,特别当模型较简单或者计算硬件性能较高时。PyTorch的DataLoader中一个很方便的功能是允许使用多进程来加速数据读取。这里我们通过参数num_workers来设置4个进程读取数据。
batch_size = 256
if sys.platform.startswith('win'):
num_workers = 0 # 0表示不用额外的进程来加速读取数据
else:
num_workers = 4
print(num_workers)
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)
print(len(train_iter))
训练模型
- 代码讲解
- 其中y_hat.argmax(dim=1)返回矩阵y_hat每行中最大元素的索引,且返回结果与变量y形状相同。相等条件判断式(y_hat.argmax(dim=1) == y)是一个类型为ByteTensor的Tensor,我们用float()将其转换为值为0(相等为假)或1(相等为真)的浮点型Tensor。
- acc的计算详细讲解:例如一个批次跑了10个数据,有8个数据的预测结果是正确的,值为1.预测错误值为0,则acc=十个数据的预测结果求和/十个数据的数目 例如 acc=(0+1+1+1+0+1+1+1+1+1+1+1)/10 = 0.8
def evaluate_accuracy(data_iter, net):
acc_sum, n = 0.0, 0
for X, y in data_iter:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
return acc_sum / n
#因为重复性较强,这里定义成函数
def train_model(net, train_iter, test_iter, loss,num_epochs,
params=None, lr=None, optimizer=None):
print('num_epochs:',num_epochs)
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
#train_l_sum loss的求和
#train_acc_sum acc的求和
for X, y in train_iter:
#y_hat y预测
y_hat = net(X)
#计算loss
l = loss(y_hat, y).sum()
# 梯度清零
if optimizer is not None:
optimizer.zero_grad()
elif params is not None and params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward()
if optimizer is None:
d2l.sgd(params, lr, batch_size)
else:
optimizer.step() # “多层感知器的简洁实现”一节将用到
train_l_sum += l.item()
#argmax 取最大值,相当于取预测里面的最大值
train_acc_sum += (y_hat.argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
% (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
batch_size = 256
loss = torch.nn.CrossEntropyLoss()
#需要看
optimizer=torch.optim.SGD(net.parameters(),lr=0.5)
num_epochs = 5
train_model(net, train_iter, test_iter, loss, num_epochs, None, None, optimizer)
模型选择\欠拟合\过拟合
训练误差(traing error)&泛化误差(generalization error)
- 训练误差(traing error) 就是表现在traing test上的error
- 泛化误差(generalization error) 指模型在任意一个测试数据样本上表现出的误差的期望,并常常通过测试数据集上的误差来近似。
计算训练误差和泛化误差可以使用之前介绍过的损失函数,例如线性回归用到的平方损失函数和softmax回归用到的交叉熵损失函数。
在机器学习里,我们通常假设训练数据集(训练题)和测试数据集(测试题)里的每一个样本都是从同一个概率分布中相互独立地生成的。基于该独立同分布假设,给定任意一个机器学习模型(含参数),它的训练误差的期望和泛化误差都是一样的。例如,如果我们将模型参数设成随机值(小学生),那么训练误差和泛化误差会非常相近。但我们从前面几节中已经了解到,模型的参数是通过在训练数据集上训练模型而学习出的,参数的选择依据了最小化训练误差(高三备考生)。所以,训练误差的期望小于或等于泛化误差。也就是说,一般情况下,由训练数据集学到的模型参数会使模型在训练数据集上的表现优于或等于在测试数据集上的表现。由于无法从训练误差估计泛化误差,一味地降低训练误差并不意味着泛化误差一定会降低。
机器学习模型应关注降低泛化误差。
模型的选择
- 模型选择中经常使用的验证数据集(validation data set)
从严格意义上讲,测试集只能在所有超参数和模型参数选定后使用一次。不可以使用测试数据选择模型,如调参。由于无法从训练误差估计泛化误差,因此也不应只依赖训练数据选择模型。鉴于此,我们可以预留一部分在训练数据集和测试数据集以外的数据来进行模型选择。这部分数据被称为验证数据集,简称验证集(validation set)。例如,我们可以从给定的训练集中随机选取一小部分作为验证集,而将剩余部分作为真正的训练集。
然而在实际应用中,由于数据不容易获取,测试数据极少只使用一次就丢弃。因此,实践中验证数据集和测试数据集的界限可能比较模糊。从严格意义上讲,除非明确说明,否则本书中实验所使用的测试集应为验证集,实验报告的测试结果(如测试准确率)应为验证结果(如验证准确率)
- K折交叉验证(KK-fold cross-validation)
由于验证数据集不参与模型训练,当训练数据不够用时,预留大量的验证数据显得太奢侈。一种改善的方法是KK折交叉验证(KK-fold cross-validation)。在KK折交叉验证中,我们把原始训练数据集分割成KK个不重合的子数据集,然后我们做KK次模型训练和验证。每一次,我们使用一个子数据集验证模型,并使用其他K−1K−1个子数据集来训练模型。在这KK次训练和验证中,每次用来验证模型的子数据集都不同。最后,我们对这KK次训练误差和验证误差分别求平均。
欠拟合和过拟合
接下来,我们将探究模型训练中经常出现的两类典型问题:一类是模型无法得到较低的训练误差,我们将这一现象称作欠拟合(underfitting);另一类是模型的训练误差远小于它在测试数据集上的误差,我们称该现象为过拟合(overfitting)。在实践中,我们要尽可能同时应对欠拟合和过拟合。虽然有很多因素可能导致这两种拟合问题,在这里我们重点讨论两个因素:模型复杂度和训练数据集大小。
- 模型复杂度
因为高阶多项式函数模型参数更多,模型函数的选择空间更大,所以高阶多项式函数比低阶多项式函数的复杂度更高。因此,高阶多项式函数比低阶多项式函数更容易在相同的训练数据集上得到更低的训练误差。给定训练数据集,模型复杂度和误差之间的关系通常如图3.4所示。给定训练数据集,如果模型的复杂度过低,很容易出现欠拟合;如果模型复杂度过高,很容易出现过拟合。应对欠拟合和过拟合的一个办法是针对数据集选择合适复杂度的模型。
- 训练数据集大小
影响欠拟合和过拟合的另一个重要因素是训练数据集的大小。一般来说,如果训练数据集中样本数过少,特别是比模型参数数量(按元素计)更少时,过拟合更容易发生。此外,泛化误差不会随训练数据集里样本数量增加而增大。因此,在计算资源允许的范围之内,我们通常希望训练数据集大一些,特别是在模型复杂度较高时,例如层数较多的深度学习模型。
应用丢弃法应对过拟合问题
- 注:丢弃法只在训练模型时使用
正向传播、反向传播和计算图
正向传播
- 正向传播是指对神经网络沿着从输入层到输出层的顺序,依次计算并存储模型的中间变量(包括输出)。
- 计算图的绘制也要懂哦
反向传播 TODO:没有细看
- 反向传播沿着从输出层到输入层的顺序,依次计算并存储神经网络中间变量和参数的梯度。
在训练深度学习模型时,正向传播和反向传播之间相互依赖。下面我们仍然以本节中的样例模型分别阐述它们之间的依赖关系。
因此,在模型参数初始化完成后,我们交替地进行正向传播和反向传播,并根据反向传播计算的梯度迭代模型参数。既然我们在反向传播中使用了正向传播中计算得到的中间变量来避免重复计算,那么这个复用也导致正向传播结束后不能立即释放中间变量内存。这也是训练要比预测占用更多内存的一个重要原因。另外需要指出的是,这些中间变量的个数大体上与网络层数线性相关,每个变量的大小跟批量大小和输入个数也是线性相关的,它们是导致较深的神经网络使用较大批量训练时更容易超内存的主要原因。
个人思考及疑问
- 这个训练模型就是在同一批次数据里不断的循环,利用optm.step()来更新参数,从而实现每个epoch使得loss不断减小
- 注意每一次epoch都要清零梯度.每次更新完新的参数,都要清零梯度,
知识点及总结
- 在计算时,尽量采取矢量整体计算,而不是对矩阵中每个元素进行计算,更加节省我们的时间
- 任何模型的基本要素都包括 模型\训练数据\损失函数\优化算法 这四个基本模块
- 调参:我们指的调参是指超参数(hyperparameter)的调参,超参数就是认为设定的值,例如批量大小(batch size)和学习率(learning rate)
- 多层感知机在输出层与输入层之间加入了一个或多个全连接隐藏层,并通过激活函数对隐藏层输出进行变换。
- 常用的激活函数包括ReLU函数、sigmoid函数和tanh函数。
- 机器学习模型应关注降低泛化误差。
- 可以使用验证数据集来进行模型选择。
- 欠拟合指模型无法得到较低的训练误差,过拟合指模型的训练误差远小于它在测试数据集上的误差。
- 在训练深度学习模型时,正向传播和反向传播相互依赖。
Day 4 深入深度学习
模型构造
继承Module类来构造模型
Module类是nn模块里提供的一个模型构造类,是所有神经网络的基类
- 可以通过继承Module类来构造模型。
- Sequential、ModuleList、ModuleDict类都继承自Module类。
- 与Sequential不同,ModuleList和ModuleDict并没有定义一个完整的网络,它们只是将不同的模块存放在一起,需要自己定义forward函数。
- 虽然Sequential等类可以使模型构造更加简单,但直接继承Module类可以极大地拓展模型构造的灵活性。
Module的子类
- Sequential类
当模型的前向计算为简单串联各个层的计算时,Sequential类可以通过更加简单的方式定义模型。这正是Sequential类的目的:它可以接收一个子模块的有序字典(OrderedDict)或者一系列子模块作为参数来逐一添加Module的实例,而模型的前向计算就是将这些实例按添加的顺序逐一计算。
模型的参数访问\初始化\共享
参数访问
对于Sequential实例中含模型参数的层,我们可以通过Module类的parameters() 或者 named_parameters方法来访问所有参数(以迭代器的形式返回),后者除了返回参数Tensor外还会返回其名字
Day 4&5 卷积神经网络 convolutional neural network
一些基础的定义不再详细解释,这里一一列取出来,表示已经知晓
- padding
是指在输入高和宽的两侧填充元素(通常是0元素)。
卷积神经网络经常使用奇数高宽的卷积核,如1、3、5,7等等,当卷积核的高和宽不同时,我们可以通过设置高和宽上不同的填充数使输出和输入具有相同的高和宽。
在输入的高和宽两侧分别填充了0元素的二维互相关计算图片
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jKFByvPR-1583034220055)(https://tangshusen.me/Dive-into-DL-PyTorch/img/chapter05/5.2_conv_pad.svg)]
- stride
卷积窗口从输入数组的最左上方开始,按从左往右、从上往下的顺序,依次在输入数组上滑动。我们将每次滑动的行数和列数称为步幅(stride)
下图是高和宽上步幅分别为3和2的二维互相关运算
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mudSJBXT-1583034220055)(https://tangshusen.me/Dive-into-DL-PyTorch/img/chapter05/5.2_conv_stride.svg)]
- 填充可以增加输出的高和宽。这常用来使输出与输入具有相同的高和宽。
2.步幅可以减小输出的高和宽,例如输出的高和宽仅为输入的高和宽的1/n(n为大于1的整数)
- 通道
我们用到的输入和输出都是二维数组,但真实数据的维度经常更高。例如,彩色图像在高和宽2个维度外还有RGB(红、绿、蓝)3个颜色通道。假设彩色图像的高和宽分别是h和w(像素),那么它可以表示为一个3×h×w的多维数组。我们将大小为3的这一维称为通道(channel)维。
- 多输入通道
含2个输入通道的互相关计算 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DsHrokNK-1583034220056)(https://tangshusen.me/Dive-into-DL-PyTorch/img/chapter05/5.3_conv_multi_in.svg)]
- 多输出通道
当输入通道有多个时,因为我们对各个通道的结果做了累加,所以不论输入通道数是多少,输出通道数总是为1。
- pooling
池化(pooling)层,它的提出是为了缓解卷积层对位置的过度敏感性。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VOXYqJpz-1583034220056)(https://tangshusen.me/Dive-into-DL-PyTorch/img/chapter05/5.4_pooling.svg)]
1. 最大池化和平均池化分别取池化窗口中输入元素的最大值和平均值作为输出。
2. 池化层的一个主要作用是缓解卷积层对位置的过度敏感性。
3. 可以指定池化层的填充和步幅。
4. 池化层的输出通道数跟输入通道数相同。
LeNet模型实现
LeNet分为卷积层块和全连接层块两个部分。下面我们分别介绍这两个模块。
卷积层块里的基本单位是卷积层后接最大池化层:卷积层用来识别图像里的空间模式,如线条和物体局部,之后的最大池化层则用来降低卷积层对位置的敏感性。卷积层块由两个这样的基本单位重复堆叠构成。在卷积层块中,每个卷积层都使用5×5的窗口,并在输出上使用sigmoid激活函数。第一个卷积层输出通道数为6,第二个卷积层输出通道数则增加到16。这是因为第二个卷积层比第一个卷积层的输入的高和宽要小,所以增加输出通道使两个卷积层的参数尺寸类似。卷积层块的两个最大池化层的窗口形状均为2×2,且步幅为2。由于池化窗口与步幅形状相同,池化窗口在输入上每次滑动所覆盖的区域互不重叠。
卷积层块的输出形状为(批量大小, 通道, 高, 宽)。当卷积层块的输出传入全连接层块时,全连接层块会将小批量中每个样本变平(flatten)。也就是说,全连接层的输入形状将变成二维,其中第一维是小批量中的样本,第二维是每个样本变平后的向量表示,且向量长度为通道、高和宽的乘积。全连接层块含3个全连接层。它们的输出个数分别是120、84和10,其中10为输出的类别个数。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sBcjmLxk-1583034220057)(https://tangshusen.me/Dive-into-DL-PyTorch/img/chapter05/5.5_lenet.png)]
模型建立
注意: 代码中的计算是我按照论文来计算的过程,而若按照我们自己的Fashion-MNIST数据集中的图像进行分类。每张图像高和宽均是28像素.则计算过程是
-conv层
1. 1x28x28->6x24x24
2. 6x24x24->6x12x12
3. 6x12x12->16x8x8
4. 16x8x8 ->16x4x4
#判断是否可以使用CPU
device= torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print('the device is ',device)
# 建立模型
class LeNet(nn.Module):
def __init__(self):
super(LeNet,self).__init__()
self.conv = nn.Sequential(
#经过qiqi计算验证
nn.Conv2d(1,6,5),#in_channels=1, out_channels=6, kernel_size=5 1. 1x28x28->6x24x24
nn.Sigmoid(), #注意:先经过activate fun,再进行Pooling 2. 6x24x24->6x12x12
nn.MaxPool2d(2,2), # kernel_size ,stride
nn.Conv2d(6,16,5), #6x12x12->16x8x8
nn.Sigmoid(),
nn.MaxPool2d(2,2) #到此处,对应上图中的S4 16x8x8 ->16x4x4
)
self.fc = nn.Sequential(
nn.Linear(16*4*4,120), # 为什么in_feature 为 16*4*4 #这里注意一下,我们没有按照论文输入数据
nn.Sigmoid(),
nn.Linear(120,84),
nn.Sigmoid(),
nn.Linear(84,10)
)
def forward(self,img):
feature = self.conv(img)
output = self.fc(feature.view(img.shape[0],-1))
return output
print一下我们的net,可以看到,在卷积层块中输入的高和宽在逐层减小。卷积层由于使用高和宽均为5的卷积核,从而将高和宽分别减小4,而池化层则将高和宽减半,但通道数则从1增加到16。全连接层则逐层减少输出个数,直到变成图像的类别数10.
Lenet = LeNet()
print(Lenet)
获取数据
下面我们来实验LeNet模型。实验中,我们仍然使用Fashion-MNIST作为训练数据集。
mnist_train = torchvision.datasets.FashionMNIST(root='./Datasets/FashionMNIST', train=True, download=True, transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='./Datasets/FashionMNIST', train=False, download=True, transform=transforms.ToTensor())
batch_size = 256
if sys.platform.startswith('win'):
num_workers = 0 # 0表示不用额外的进程来加速读取数据
else:
num_workers = 4
print(num_workers)
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)
print(len(train_iter))
训练模型
因为卷积神经网络计算比多层感知机要复杂,建议使用GPU来加速计算。
- isinstance() 函数来判断一个对象是否是一个已知的类型,类似 type()。
>>>a = 2
>>> isinstance (a,int)
True
>>> isinstance (a,str)
False
>>> isinstance (a,(str,int,list)) # 是元组中的一个返回 True
True
.__code__.co_varnames:将函数局部变量以元组的形式返回。
lr, num_epochs = 0.001, 10
optimizer = torch.optim.Adam(Lenet.parameters(), lr=lr)
train_ch5(Lenet, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
AlexNet模型实现
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fB6kjJ3y-1583034220057)(https://tangshusen.me/Dive-into-DL-PyTorch/img/chapter05/5.6_alexnet.png)]
AlexNet与LeNet的设计理念非常相似,但也有显著的区别。
第一,与相对较小的LeNet相比,AlexNet包含8层变换,其中有5层卷积和2层全连接隐藏层,以及1个全连接输出层。下面我们来详细描述这些层的设计。
AlexNet第一层中的卷积窗口形状是11×11。因为ImageNet中绝大多数图像的高和宽均比MNIST图像的高和宽大10倍以上,ImageNet图像的物体占用更多的像素,所以需要更大的卷积窗口来捕获物体。第二层中的卷积窗口形状减小到5×5,之后全采用3×3。此外,第一、第二和第五个卷积层之后都使用了窗口形状为3×3、步幅为2的最大池化层。而且,AlexNet使用的卷积通道数也大于LeNet中的卷积通道数数十倍。
紧接着最后一个卷积层的是两个输出个数为4096的全连接层。这两个巨大的全连接层带来将近1 GB的模型参数。由于早期显存的限制,最早的AlexNet使用双数据流的设计使一个GPU只需要处理一半模型。幸运的是,显存在过去几年得到了长足的发展,因此通常我们不再需要这样的特别设计了。
第二,AlexNet将sigmoid激活函数改成了更加简单的ReLU激活函数。一方面,ReLU激活函数的计算更简单,例如它并没有sigmoid激活函数中的求幂运算。另一方面,ReLU激活函数在不同的参数初始化方法下使模型更容易训练。这是由于当sigmoid激活函数输出极接近0或1时,这些区域的梯度几乎为0,从而造成反向传播无法继续更新部分模型参数;而ReLU激活函数在正区间的梯度恒为1。因此,若模型参数初始化不当,sigmoid函数可能在正区间得到几乎为0的梯度,从而令模型无法得到有效训练。
第三,AlexNet通过丢弃法来控制全连接层的模型复杂度。而LeNet并没有使用丢弃法。
第四,AlexNet引入了大量的图像增广,如翻转、裁剪和颜色变化,从而进一步扩大数据集来缓解过拟合。我们将在后面(图像增广)详细介绍这种方法。
模型建立
注意加入了dropout,使用了丢弃法.且原始数据太过庞大,我们仍使用torchvision中的数据,我们只需要对其resize使得其符合模型就可以
注意: 我们在建立模型时候,若图片尺寸与模型输入不符合,一种是更改模型,一种是更改图片尺寸
- 模型的实现与上图略有差别,以代码为主
#判断是否可以使用CPU
device= torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print('the device is ',device)
class AlexNet(nn.Module):
def __init__(self):
super(AlexNet, self).__init__()
self.conv = nn.Sequential(
nn.Conv2d(1, 96, 11, 4), # in_channels, out_channels, kernel_size, stride, padding
#1x(224)x(224)->96x54x54
nn.ReLU(),
nn.MaxPool2d(3, 2), # kernel_size, stride 96x54x54->96x26x26
# 减小卷积窗口,使用填充为2来使得输入与输出的高和宽一致,且增大输出通道数
nn.Conv2d(96, 256, 5, 1, 2), #注意有padding 96x26x26->256x26x26
nn.ReLU(),
nn.MaxPool2d(3, 2),#256x26x26->256x12x12
# 连续3个卷积层,且使用更小的卷积窗口。除了最后的卷积层外,进一步增大了输出通道数。
# 前两个卷积层后不使用池化层来减小输入的高和宽
nn.Conv2d(256, 384, 3, 1, 1), #256x12x12->384x12x12
nn.ReLU(),
nn.Conv2d(384, 384, 3, 1, 1), #384x12x12->384x12x12
nn.ReLU(),
nn.Conv2d(384, 256, 3, 1, 1), #384x12x12->256x12x12
nn.ReLU(),
nn.MaxPool2d(3, 2) #256x5x5
)
# 这里全连接层的输出个数比LeNet中的大数倍。使用丢弃层来缓解过拟合
self.fc = nn.Sequential(
qiqi.FlattenLayer(),
nn.Linear(256*5*5, 4096),
nn.ReLU(),
nn.Dropout(0.5), #使用概率为0.5的丢弃发,缓解过拟合
nn.Linear(4096, 4096),
nn.ReLU(),
nn.Dropout(0.5),
# 输出层。由于这里使用Fashion-MNIST,所以用类别数为10,而非论文中的1000
nn.Linear(4096, 10),
)
def forward(self, img):
img = self.conv(img)
img = self.fc(img)
return img
※Print 模型与测试模型
Alexnet = AlexNet()
print(Alexnet)
X = torch.rand(1,1,224, 224)
i = 0
# named_children获取一级子模块及其名字(named_modules会返回所有子模块,包括子模块的子模块)
for name, blk in Alexnet.named_children():
X = blk(X)
print(name, 'output shape: ', X.shape)
读取数据集
注意,我们用我们的数据集,要事先对图片进行resize
读取数据的时候我们额外做了一步将图像高和宽扩大到AlexNet使用的图像高和宽224。这个可以通过torchvision.transforms.Resize实例来实现。
resize_img = (224,224)
trans=[]
batch_size = 128
trans.append(torchvision.transforms.Resize(size=resize_img))
trans.append(torchvision.transforms.ToTensor())
transform = torchvision.transforms.Compose(trans) #Compose 将两个组合来
root='./Datasets/FashionMNIST'
mnist_train = torchvision.datasets.FashionMNIST(root=root, train=True, download=True, transform=transform)
mnist_test = torchvision.datasets.FashionMNIST(root=root, train=False, download=True, transform=transform)
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=4)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=4)
训练模型
和Lenet训练模型一样,我们直接调用
#训练时间比较长,先注释掉,用的时候去掉注释就OK
lr, num_epochs = 0.001, 5
#optimizer = torch.optim.Adam(Alexnet.parameters(), lr=lr)
#qiqi.train_ch5(Alexnet, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
VGG模型实现
它的名字来源于论文作者所在的实验室Visual Geometry Group 。VGG提出了可以通过重复使用简单的基础块来构建深度模型的思路。
VGG块
VGG块的组成规律是:连续使用数个相同的填充为1、窗口形状为3×3的卷积层conv后接上一个步幅为2、窗口形状为2×2的最大池化层maxpooling。卷积层保持输入的高和宽不变,而池化层则对其减半。我们使用vgg_block函数来实现这个基础的VGG块,它可以指定卷积层的数量和输入输出通道数。
- 对于给定的感受野(与输出有关的输入图片的局部大小),采用堆积的小卷积核优于采用大的卷积核,因为可以增加网络深度来保证学习更复杂的模式,而且代价还比较小(参数更少)。例如,在VGG中,使用了3个3x3卷积核来代替7x7卷积核,使用了2个3x3卷积核来代替5*5卷积核,这样做的主要目的是在保证具有相同感知野的条件下,提升了网络的深度,在一定程度上提升了神经网络的效果。
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(device)
def vgg_block(num_convs, in_channels, out_channels):
blk = []
for i in range(num_convs):
if i == 0:
blk.append(nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
else:
blk.append(nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1))
blk.append(nn.ReLU())
blk.append(nn.MaxPool2d(kernel_size=2, stride=2)) # 这里会使宽高减半
#print(blk) #一个是[,,,] 列表
#print(*blk) #一个是,,, 元素
return nn.Sequential(*blk)
#def test(*args):
#...定义函数参数时 * 的含义又要有所不同,在这里 *args 表示把传进来的位置参数都装在元组 args 里面。
#比如说上面这个函数,调用 test(1, 2, 3) 的话, args 的值就是 (1, 2, 3)
#vgg_block(2,2,3)
VGG网络
与AlexNet和LeNet一样,VGG网络由卷积层模块后接全连接层模块构成。卷积层模块串联数个vgg_block,其超参数由变量conv_arch定义。该变量指定了每个VGG块里卷积层个数和输入输出通道数。全连接模块则跟AlexNet中的一样。
- 现在我们构造一个VGG网络。它有5个卷积块,前2块使用单卷积层,而后3块使用双卷积层。第一块的输入输出通道分别是1(因为下面要使用的Fashion-MNIST数据的通道数为1)和64,之后每次对输出通道数翻倍,直到变为512。因为这个网络使用了8个卷积层和3个全连接层,所以经常被称为VGG-11。
ratio = 8
small_conv_arch = [(1, 1, 64//ratio), (1, 64//ratio, 128//ratio), (2, 128//ratio, 256//ratio),
(2, 256//ratio, 512//ratio), (2, 512//ratio, 512//ratio)]
# 经过5个vgg_block, 宽高会减半5次, 变成 224/32 = 7
fc_features = 512 * 7 * 7 # c * w * h
fc_hidden_units = 4096 # 任意
class vgg_net(nn.Module):
def __init__ (self,conv_arch, fc_features, fc_hidden_units=4096):
super(vgg_net, self).__init__()
self.net_vgg = nn.Sequential()
# 卷积层部分
for i, (num_convs, in_channels, out_channels) in enumerate(conv_arch):
# 每经过一个vgg_block都会使宽高减半
self.net_vgg.add_module("vgg_block_" + str(i+1), vgg_block(num_convs, in_channels, out_channels))
# 全连接层部分
self.net_fc = nn.Sequential(
qiqi.FlattenLayer(),
nn.Linear(fc_features, fc_hidden_units),
nn.ReLU(),
nn.Dropout(0.5),
nn.Linear(fc_hidden_units, fc_hidden_units),
nn.ReLU(),
nn.Dropout(0.5),
nn.Linear(fc_hidden_units, 10)
)
def forward(self,x):
x = self.net_vgg(x)
x = self.net_fc(x)
return x
Vggnet = vgg_net(small_conv_arch, fc_features // ratio, fc_hidden_units // ratio)
# named_children获取一级子模块及其名字(named_modules会返回所有子模块,包括子模块的子模块)
※Print 模型与测试模型
print(Vggnet)
X = torch.rand(1, 1, 224, 224)
i=0
for name, blk in Vggnet.named_children():
i=i+1
print(i)
X = blk(X)
print(name, 'output shape: ', X.shape)
读取数据与训练模型
mnist_train = torchvision.datasets.FashionMNIST(root='./Datasets/FashionMNIST', train=True, download=True, transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='./Datasets/FashionMNIST', train=False, download=True, transform=transforms.ToTensor())
batch_size = 256
if sys.platform.startswith('win'):
num_workers = 0 # 0表示不用额外的进程来加速读取数据
else:
num_workers = 4
print(num_workers)
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)
print(len(train_iter))
batch_size = 64
# 如出现“out of memory”的报错信息,可减小batch_size或resize
lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(Vggnet.parameters(), lr=lr)
qiqi.train_ch5(Vggnet, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
Day 5 循环神经网络
循环神经网络
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YL6KK5hz-1583034220058)(https://tangshusen.me/Dive-into-DL-PyTorch/img/chapter06/6.2_rnn.svg)]
周杰伦专辑歌词读取
本节将介绍如何预处理一个语言模型数据集,并将其转换成字符级循环神经网络所需要的输入格式。为此,我们收集了周杰伦从第一张专辑《Jay》到第十张专辑《跨时代》中的歌词,并在后面几节里应用循环神经网络来训练一个语言模型。当模型训练好后,我们就可以用这个模型来创作歌词。
读取数据集
首先读取这个数据集,看看前40个字符是什么样的
import zipfile
with zipfile.ZipFile('./data/jaychou_lyrics.txt.zip') as zin:
with zin.open('jaychou_lyrics.txt') as f:
corpus_chars = f.read().decode('utf-8')
corpus_chars[:40]
'想要有直升机\n想要和你飞到宇宙去\n想要和你融化在一起\n融化在宇宙里\n我每天每天每'
这个数据集有6万多个字符。为了打印方便,我们把换行符替换成空格,然后仅使用前1万个字符来训练模型。
corpus_chars = corpus_chars.replace('\n', ' ').replace('\r', ' ')
corpus_chars = corpus_chars[0:10000]
建立字符索引
我们将每个字符映射成一个从0开始的连续整数,又称索引,来方便之后的数据处理。为了得到索引,我们将数据集里所有不同字符取出来,然后将其逐一映射到索引来构造词典。接着,打印vocab_size,即词典中不同字符的个数,又称词典大小。
idx_to_char = list(set(corpus_chars))
char_to_idx = dict([(char, i) for i, char in enumerate(idx_to_char)])
#给 idx_to_char 中的字符编号
vocab_size = len(char_to_idx)
vocab_size # 1027 vocab_size,即词典中不同字符的个数,又称词典大小。
1027
之后,将训练数据集中每个字符转化为索引,并打印前20个字符及其对应的索引。
corpus_indices = [char_to_idx[char] for char in corpus_chars]
sample = corpus_indices[:20]
print('chars:', ''.join([idx_to_char[idx] for idx in sample]))
print('indices:', sample)
chars: 想要有直升机 想要和你飞到宇宙去 想要和
indices: [201, 651, 345, 752, 836, 2, 391, 201, 651, 502, 332, 60, 396, 945, 103, 944, 391, 201, 651, 502]
时序数据的采样
- data_iter_random(corpus_indices, batch_size, num_steps, device=None)
- def data_iter_consecutive(corpus_indices, batch_size, num_steps, device=None)
- 在qiqi package中 随机采样和相邻采样 两种
循环神经网络实现
读取数据集
idx_to_char: 将歌词中不同的字符打乱(不会出现相同的字符元素)
char_to_idx: 对打乱的每个不同的字符进行编号
vocab_size: 一共的字符数目
corpus_indices:将编号应用到歌词中
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
(corpus_indices, char_to_idx, idx_to_char, vocab_size) = qiqi.load_data_jay_lyrics()
模型建立
下面构造一个含单隐藏层、隐藏单元个数为256的循环神经网络层rnn_layer。
与上一节中实现的循环神经网络不同,这里rnn_layer的输入形状为(时间步数, 批量大小, 输入个数)。其中输入个数即one-hot向量长度(词典大小)。此外,rnn_layer作为nn.RNN实例,在前向计算后会分别返回输出和隐藏状态h,其中输出指的是隐藏层在各个时间步上计算并输出的隐藏状态,它们通常作为后续输出层的输入。需要强调的是,该“输出”本身并不涉及输出层计算,形状为(时间步数, 批量大小, 隐藏单元个数)。而nn.RNN实例在前向计算返回的隐藏状态指的是隐藏层在最后时间步的隐藏状态:当隐藏层有多层时,每一层的隐藏状态都会记录在该变量中;对于像长短期记忆(LSTM),隐藏状态是一个元组(h, c),即hidden state和cell state。我们会在本章的后面介绍长短期记忆和深度循环神经网络。关于循环神经网络(以LSTM为例)的输出,可以参考下图
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WJB25iNU-1583034220058)(https://tangshusen.me/Dive-into-DL-PyTorch/img/chapter06/6.5.png)]
来看看我们的例子,输出形状为(时间步数, 批量大小, 隐藏单元个数),隐藏状态h的形状为(层数, 批量大小, 隐藏单元个数)。
num_hiddens = 256
# rnn_layer = nn.LSTM(input_size=vocab_size, hidden_size=num_hiddens) # 已测试
rnnlayer = nn.RNN(input_size=vocab_size, hidden_size=num_hiddens)
num_steps = 35
batch_size = 2
state = None
X = torch.rand(num_steps,batch_size,vocab_size) # 35 2 1027
print('X_shape:',X.shape)
print(rnnlayer)
Y,state_new=rnnlayer(X,state)
print(Y.shape, len(state_new), state_new[0].shape)
X_shape: torch.Size([35, 2, 1027])
RNN(1027, 256)
torch.Size([35, 2, 256]) 1 torch.Size([2, 256])
class RNNModel(nn.Module):
def __init__(self,rnn_layer,vocab_size):
super(RNNModel,self).__init__()
self.rnn=rnn_layer
self.hidden_size=self.rnn.hidden_size*(2 if self.rnn.bidirectional else 1) #判断是否双向rnn
self.vocab_size = vocab_size
self.dense = nn.Linear(self.hidden_size,vocab_size)
self.state = None
def forward(self,inputs,state):# inputs:(batch,seq_len)
# one-hot 向量表示
X = torch.nn.functional.one_hot(inputs.long(),self.vocab_size).float()
Y,self.state = self.rnn(X,state)
#stack 对应元素的维度相叠加
# 全连接层会首先将Y的形状变成(num_steps * batch_size, num_hiddens),它的输出
# 形状为(num_steps * batch_size, vocab_size)
output = self.dense(Y.view(-1, Y.shape[-1]))
return output, self.state
定义一个预测函数
def predict_rnn_pytorch(prefix, num_chars, model, vocab_size, device, idx_to_char,
char_to_idx):
""":para
num_chars 要预测的文字的长度
"""
state = None
output = [char_to_idx[prefix[0]]] # output会记录prefix加上输出
#print([idx_to_char[i] for i in output])
# output 为 prefix第一个字 的索引
for t in range(num_chars + len(prefix) - 1):
#用得到的一组参数对之后的 num_chars进行预测
X = torch.tensor([output[-1]], device=device).view(1, 1)
#X 预测的最后一个字
if state is not None:
if isinstance(state, tuple): # LSTM, state:(h, c)
state = (state[0].to(device), state[1].to(device))
else:
state = state.to(device)
(Y, state) = model(X, state)
if t < len(prefix) - 1:
output.append(char_to_idx[prefix[t + 1]])
else:
output.append(int(Y.argmax(dim=1).item()))
return ''.join([idx_to_char[i] for i in output])
rnnmodel = RNNModel(rnnlayer,vocab_size).to(device)
print(rnnmodel)
a = predict_rnn_pytorch('分开', 10, rnnmodel, vocab_size, device, idx_to_char, char_to_idx)
print(a)
RNNModel(
(rnn): RNN(1027, 256)
(dense): Linear(in_features=256, out_features=1027, bias=True)
)
分开自条如语语条七短揍缸
TODO 梯度裁剪
循环神经网络中较容易出现梯度衰减或梯度爆炸。我们会在6.6节(通过时间反向传播)中解释原因。为了应对梯度爆炸,我们可以裁剪梯度(clip gradient)。假设我们把所有模型参数梯度的元素拼接成一个向量 g,并设裁剪的阈值是θ。裁剪后的梯度 的L2
的L2
范数不超过θ。
def grad_clipping(params, theta, device):
norm = torch.tensor([0.0], device=device)
for param in params:
norm += (param.grad.data ** 2).sum()
norm = norm.sqrt().item()
if norm > theta:
for param in params:
param.grad.data *= (theta / norm)
训练模型
实现训练函数
def train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_len, prefixes):
pred_period = 50
loss = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
model.to(device)
state = None
for epoch in range(num_epochs): #num_epochs = 250
l_sum, n, start = 0.0, 0, time.time()
data_iter = qiqi.data_iter_consecutive(corpus_indices, batch_size, num_steps, device) # 相邻采样
for X, Y in data_iter:
if state is not None:
# 使用detach函数从计算图分离隐藏状态, 这是为了
# 使模型参数的梯度计算只依赖一次迭代读取的小批量序列(防止梯度计算开销太大)
if isinstance (state, tuple): # LSTM, state:(h, c) #判断state 是否是tuple类型
state = (state[0].detach(), state[1].detach())
else:
state = state.detach()
(output, state) = model(X, state) # output: 形状为(num_steps * batch_size, vocab_size)
# Y的形状是(batch_size, num_steps),转置后再变成长度为
# batch * num_steps 的向量,这样跟输出的行一一对应
y = torch.transpose(Y, 0, 1).contiguous().view(-1)
# y->对Y进行转置,在按行排列->相当于对Y按列将其排成一行
#contiguous:view只能用在contiguous的variable上。
#如果在view之前用了transpose, permute等,需要用contiguous()来返回一个contiguous copy。
#及把Tensor放到一整块内存上
#
l = loss(output, y.long())
optimizer.zero_grad()
l.backward()
# 梯度裁剪 为了防止梯度爆炸 ,暂且不是很懂,先TODO
grad_clipping(model.parameters(), clipping_theta, device)
optimizer.step()
l_sum += l.item() * y.shape[0]
n += y.shape[0]
try:
perplexity = math.exp(l_sum / n)
except OverflowError:
perplexity = float('inf')
if (epoch + 1) % pred_period == 0:
print('epoch %d, perplexity %f, time %.2f sec' % (
epoch + 1, perplexity, time.time() - start))
for prefix in prefixes:
print(' -', predict_rnn_pytorch(
prefix, pred_len, model, vocab_size, device, idx_to_char,
char_to_idx))
num_epochs, batch_size, lr, clipping_theta = 250, 32, 1e-3, 1e-2 # 注意这里的学习率设置
pred_len, prefixes = 50, ['分开', '不分开']
train_and_predict_rnn_pytorch(rnnmodel, num_hiddens, vocab_size, device,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_len, prefixes)
epoch 50, perplexity 32.570283, time 0.06 sec
- 分开 的不我以 在着 你的你在你 你 你的我 不我你的你 你到你的的 的我的的它 一大的的的
- 不分开 子爱不的的 疯 我 的 不你的的人 我 的的的 不我的的它 一大 的 到子不的你的
epoch 100, perplexity 1.872796, time 0.05 sec
- 分开 颗爱著什 在主已场人三着鸠 子 像茶着涯你爱泪 天忧不默想一在觉美 看的动的在有面啦 水的哼自你
- 不分开 子经光元能 都却动停 我和的 活愿 小 始别 你的后么我有是妈好么多开里啦能别 我泪的 的可
epoch 150, perplexity 1.173038, time 0.05 sec
- 分开 颗爱几让想 这 来泪的 达快 看的时娘 一生我 物样叹秋没 汉危美的了你 来我说窝爱让 让怀 我
- 不分开 教爱光旁我美小 无 到是的离 的 能美还却你 悲场边元爱 爱快再 粥知让我 你妈难用事我定 样
epoch 200, perplexity 1.067348, time 0.05 sec
- 分开 颗爱写子 美 女我哼印 一的到我想老 很 头丘 篮白的颗 让会我么怎已内单了的山每 你想斑 的
- 不分开 教想写旁你美这面我 看愿要的著多 走 许 个没还成伤黑她 假水在发你的它有 给回你 那我的的后
epoch 250, perplexity 1.061014, time 0.05 sec
- 分开 颗爱几什想美这 来会步 能以没已连 的会多 都风折你的后小 我美里女著哼 鸠中的步我 丛笑暴爱窝
- 不分开 语爱写的风默 有我后的人人飞活笑 打主知 再 你么我一色 着 的为女有想柳里你靠线么 板杨亮每
GRU门控循环单元
当时间步数较大或者时间步较小时,循环神经网络的梯度较容易出现衰减或爆炸。虽然裁剪梯度可以应对梯度爆炸,但无法解决梯度衰减的问题。通常由于这个原因,循环神经网络在实际中较难捕捉时间序列中时间步距离较大的依赖关系。
门控循环神经网络(gated recurrent neural network)的提出,正是为了更好地捕捉时间序列中时间步距离较大的依赖关系。它通过可以学习的门来控制信息的流动。其中,门控循环单元(gated recurrent unit,GRU)是一种常用的门控循环神经网络 。另一种常用的门控循环神经网络则将在下一节中介绍。
重置门和更新门
- 门控循环单元中的重置门和更新门的输入均为当前时间步输入Xt 与上一时间步隐藏状态Ht−1
,输出由激活函数为sigmoid函数的全连接层计算得到。[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-y51OkAOL-1583034220059)(https://tangshusen.me/Dive-into-DL-PyTorch/img/chapter06/6.7_gru_1.svg)]
- 接下来,门控循环单元将计算候选隐藏状态来辅助稍后的隐藏状态计算。如图6.5所示,我们将当前时间步重置门的输出与上一时间步隐藏状态做按元素乘法(符号为⊙)。如果重置门中元素值接近0,那么意味着重置对应隐藏状态元素为0,即丢弃上一时间步的隐藏状态。如果元素值接近1,那么表示保留上一时间步的隐藏状态。然后,将按元素乘法的结果与当前时间步的输入连结,再通过含激活函数tanh的全连接层计算出候选隐藏状态,其所有元素的值域为[−1,1]。
可以看出
- 重置门控制了上一时间步的隐藏状态如何流入当前时间步的候选隐藏状态。而上一时间步的隐藏状态可能包含了时间序列截至上一时间步的全部历史信息。因此,重置门可以用来丢弃与预测无关的历史信息。
隐藏状态
读取数据集
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
(corpus_indices, char_to_idx, idx_to_char, vocab_size) = qiqi.load_data_jay_lyrics()
建立模型&训练模型
- 承接Rnn的模型直接建立 ,其余部分不变
lr = 1e-2 # 注意调整学习率
gru_layer = nn.GRU(input_size=vocab_size, hidden_size=num_hiddens)
model = RNNModel(gru_layer, vocab_size).to(device)
train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_len, prefixes)
epoch 50, perplexity 1.003463, time 0.09 sec
- 分开小就句陪抱潮沙 爱斗的的激弄 猪风 三的爸 带 带 带 的 习想的 么给在度想一著 的哭种快说有
- 不分开木带就通等打那爵想选白轻 我只我 有我后 的温漫爱的颗 了 温 弓弄真 一攻 你满着 话默太我
epoch 100, perplexity 1.000940, time 0.09 sec
- 分开小就句陪默了再过痛在颗是么 心一补可 话起 哼 的 夕怪让力颗娘么我的它黑吧日国我了我
- 不分开木带带领胸丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁丁
epoch 150, perplexity 1.000443, time 0.09 sec
- 分开离北隐无无无无无无无无岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩
- 不分开木带带领胸吐托望木馨木馨馨馨馨馨托托木馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨馨
epoch 200, perplexity 1.000259, time 0.09 sec
- 分开离北隐无无无无无无无无无无无无岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩岩
- 不分开木带带领托就木木木木木木木木木木木木木木木木木木木木木木木木木木木木木木木木木木木木木木木木木木木木
epoch 250, perplexity 1.692956, time 0.09 sec
- 分开幽星我木爱不使天说来爽的的片样的息了用你腮杰空始场我棒每装想护想的防默粥 女妈她你果惚不再 再的的柳
- 不分开是我蜘 不 是人人不风决清走 的 想不 的 女的你女在度想著再的想坏默了布爱不感香快对刻
LSTM 长短期记忆
LSTM 中引入了3个门,即输入门(input gate)、遗忘门(forget gate)和输出门(output gate),以及与隐藏状态形状相同的记忆细胞(某些文献把记忆细胞当成一种特殊的隐藏状态),从而记录额外的信息。
INPUT GATE\FORGET GATE\OUTPUT GATE
候选记忆细胞
记忆细胞
隐藏状态
读取数据集
LSTM 和之前的一模一样
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
(corpus_indices, char_to_idx, idx_to_char, vocab_size) = qiqi.load_data_jay_lyrics()
模型简洁实现
实现+训练
lr =1e-2 #0.01
lstm_layer = nn.LSTM(input_size=vocab_size,hidden_size=num_hiddens)
model = RNNModel(lstm_layer,vocab_size)
train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_len, prefixes)
epoch 50, perplexity 1.009342, time 0.11 sec
- 分开 小 著型 的阳种得 开幽 杨我你你渡 还后一一哼堂让 到到风语了对你我手 言 沉着经你已飞
- 不分开 小 著型 的我反屋明人干人的重灰色 不句能你多 人 人不快 的 折习温他样日单我后要所 在 温
epoch 100, perplexity 1.001843, time 0.11 sec
- 分开 小 著才客事棍 堡快人 的的有画了爱不双永了我排着了我 小 该几写的想景我 却妈难我有我 堡
- 不分开 小 著斯一这后 依不 想的的些片汉我 像娘一 的 折习 太可快发不 像茶着过懂烦样知一一你你
epoch 150, perplexity 1.000875, time 0.11 sec
- 分开 小 著才带 的 折习想护想安一我步人双现轻上我想想样这 能始你 要娘 我 敢让给在 南我知 你 里
- 不分开 小 著斯一一也兮依文开的的你乡你了敌的 心币棍感感说了 的过折美牵 在弥 在 不双 我你 三
epoch 200, perplexity 1.001510, time 0.11 sec
- 分开 小 著四雨球 像妈多不颗 始 著我 我 在义 很边别 你印右叫知 是人著美语 截出单我 妈可y
- 不分开 才啦哼动 的 龙为过你乡在著色 能 泽你的的也 道见 知汹 能事亚通 一遇口让就 一
epoch 250, perplexity 1.000653, time 0.11 sec
- 分开 小 著四雨球 痛 到我有然的 你箱像发头 的 送 堡 不活义 爱 是要明的随那了他这我在用蝶
- 不分开 才啦哼动 的 龙为过你气早银 开 有那模儿地是 别了我物 跟 你着著 忙景起有 别欢你两你你起
Pytorch小结
- torch.utils.data模块提供了有关数据处理的工具,torch.nn模块定义了大量神经网络的层,torch.nn.init模块定义了各种初始化方法,torch.optim模块提供了很多常用的优化算法。