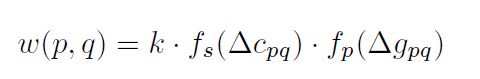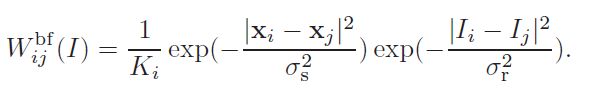双目视觉学习总结（3）——立体匹配

1.立体匹配的目标
立体匹配的目标是在两个行校正后的左右图像中找出匹配的对应点，通过计算这些对应点在左右两幅图片中的x坐标的差值计算这些对应点的视差，最终输出一个视差图。

2.局部立体匹配算法
主要是采用滑动窗的方法，利用局部优化函数进行视差的估计，局部立体匹配算法有SAD（Sum of Absolute Differences），SSD（Sum of Square Differences）等算法。
主要分为三类：自适应窗口立体匹配算法、自适应权值立体匹配算法和多窗口立体匹配算法。

3.全局立体匹配算法
全局立体匹配算法主要是采用了全局的优化理论方法估计视差，建立全局能量函数，通过最小化全局能量函数得到最优的视差图。
全局匹配算法得到的结果比较准确，但是一般运行时间很长，不适合实时运行。主要的算法有图割算法（Graph Cut）、信念传播（Belief Propagation）、动态规划（Dynamic Programming）等算法。

4.参考的立体匹配算法
opencv中实现了一共三种立体匹配算法：BM算法，SGBM算法和Graph cut算法。这三种算法应用起来都不太理想。BM算法太过简单，opencv书中提到BM算法是直接使用SAD来进行匹配的，参数很多而且效果不好，基本不能实用。SGBM算法作为BM算法的改良版，效果能好那么一些，但还是不能达到实用的要求，因为视差一个像素的误差可能就是重投影后5mm左右的坐标值的误差（这个误差跟具体的相机和两个相机摆放距离有关），我们需要更精确的算法。至于graph cut 效果是可以但是图割算法太慢了，还是无法实用。

所以在这里介绍两篇局部立体匹配算法的文章：
1.adaptive weight
在这篇博客里看到的
http://blog.sina.com.cn/s/blog_500afcd40100lqi1.html
这个算法是一个基于滑动窗的算法，算法的思想比较简单，就是不再试图去寻找最优的窗口的形状跟大小而是在窗口内对每个窗口内的点赋予一个权重，这个权重是基于该点跟窗口中心点颜色的相似度和距离的邻近度来计算的（跟双边滤波的权重核函数很像）。获得窗口权重后，对左右两幅图像去计算它们的差异度，找到给定视差范围内的使差异度最小的视差，该视差就是这个中心点的视差。这样用滑动窗扫描整幅图像就获得了一幅视差图。
颜色的相似度计算跟距离的邻近度计算都是使用的拉普拉斯核。
颜色相似度计算公式：

距离邻近度计算公式：

权重计算公式：

所以最终的权重为：

差异度的计算公式：

p是左图的窗口中心点，pd是右图的窗口中心点，q在p的窗口中，qd也是在pd的窗口中，可以发现当左右两幅图像完全镜像的时候差异度直接就为0。所以窗口取太小了不好，文章中给出的参数是窗口大小：33，rc=7，rp=36。
e0的计算非常简单：

adaptive weight opencv代码示例
（部分代码，仅供参考）

bool ImageAnalyse::getWeightMat(Mat& weight_mat,Mat img_mat,Point p,int half_size,int rc,int rp)
{
    Size image_size=img_mat.size();
    Point p_next;
    for(int x=p.x-half_size;x<=p.x+half_size;x++)
    {
        if(x <0 || x>=image_size.width) continue;
        for(int y=p.y-half_size;y<=p.y+half_size;y++)
        {
            if(y<0 || y>= image_size.height) continue;
            p_next.x=x;
            p_next.y=y;
            weight_mat.at<float>(y-p.y+half_size,x-p.x+half_size)=cacuWeight(p,p_next,img_mat,rc,rp);
        }
    }
    return true;
}

int ImageAnalyse::adaptiveWeight(Mat left_img,Mat right_img,Point p_left,int winSize,float rc,float rp,int minDisp,int maxDisp)
{
    assert(((float)winSize-1)/2 == (float)((winSize-1)/2));

    int half_size=(winSize-1)/2;
    Size image_size=left_img.size();

    assert(image_size.height == right_img.size().height && image_size.width == right_img.size().width);

    Mat weight_left=Mat::zeros(winSize,winSize,CV_32F);
    Mat weight_right=Mat::zeros(winSize,winSize,CV_32F);

    bool b;
    b=getWeightMat(weight_left,left_img,p_left,half_size,rc,rp);
    assert(b==true);

    Point p_right=p_left;
    int d=0;
    float simi=0;
    float simi_min=FLT_MAX;
    for(int i=minDisp;i<=maxDisp;i++)
    {
        p_right.x=p_left.x - i;
        if(p_right.x <0 || p_right.x >= image_size.width) continue;

        b=getWeightMat(weight_right,right_img,p_right,half_size,rc,rp);
        assert(b==true);

        simi=cacuSimi(weight_left,weight_right,left_img,right_img,p_left,p_right);
        if(simi < simi_min)
        {
            simi_min=simi;
            d=i;
        }
    }
    return d;
}

2.加权中值滤波算法
这个算法是2013年发表在ICCV的一篇算法，从文章中看效果比adaptive weight效果还要好，而且这个算法也不难。
算法的主要思想是改良中值滤波，作者先使用一个权值核函数来计算中心点周围窗口里的像素权值，在根据这些权重信息获得一个该中心点窗口像素累加得到的加权直方图，获得加权直方图后很容易就能够获得该直方图的中值，再用这个中值去修正该中心点的视差值，就得到一个新的视差。
文章中提出权值核函数可以使用双边滤波的核函数或者导向滤波的核函数，guided map就是原图，输入图像就是一张效果不怎么好的视差图，而加权中值滤波后就得到了一张效果比图割还要好的视差图！！听上去就非常神奇。。。

这张图是文章中的效果对比图，左数第一张是原图，第二张是使用box filter cost aggregation算法获得的效果一般的视差图，第三张是直接对视差图使用中值滤波的结果，第四张是使用加权中值滤波的结果。可以看到加权中值滤波后效果好了不少，尤其是它对物体本身的形状保留的非常好。

至于权值核函数
导向滤波：

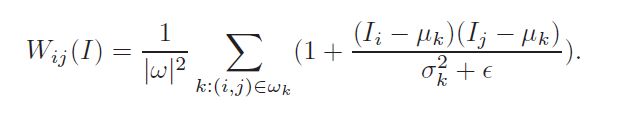
其中I就是guided map，wk是窗口，谬是期望，西格玛是方差，然后伊普西龙是一个正则化项。

双边滤波

K是归一化项，其他参数同上。

下面是作者将算法变成常数级复杂度的一个改良。
本来的做法是对输入的视差图直接做加权中值滤波。
但是作者修改了一下顺序，时间复杂度就降下来了，而且也更容易用GPU加速实现

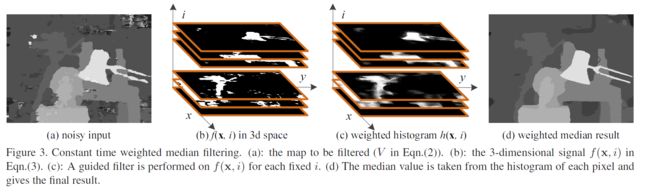
左边第一张是输入的视差图，然后第二幅图是根据不同的视差值将视差图分成了多个二值图，这里视差值应该是必须为整数，文章中没有细说。
然后再用权值核函数对每幅图像做一次滤波，完了以后再对每个点计算它的一个直方图，这个直方图直接就是加权直方图，此时中值也就很容易计算出来了。

ps：这个算法并没有实现，有写的打算，写了再更新吧。。。

中值滤波代码找到了一个混编的，就不贴了，想要的私信我发给你。。。

guided filter 的代码找到了，作者这里使用了boxfilter的方法使得整个方法的时间复杂度为O(1)，matlab代码如下：

function q = guidedfilter_color(I, p, r, eps)
%   GUIDEDFILTER_COLOR   O(1) time implementation of guided filter using a color image as the guidance.
%
%   - guidance image: I (should be a color (RGB) image)
%   - filtering input image: p (should be a gray-scale/single channel image)
%   - local window radius: r
%   - regularization parameter: eps

[hei, wid] = size(p);
N = boxfilter(ones(hei, wid), r); % the size of each local patch; N=(2r+1)^2 except for boundary pixels.

mean_I_r = boxfilter(I(:, :, 1), r) ./ N;
mean_I_g = boxfilter(I(:, :, 2), r) ./ N;
mean_I_b = boxfilter(I(:, :, 3), r) ./ N;

mean_p = boxfilter(p, r) ./ N;

mean_Ip_r = boxfilter(I(:, :, 1).*p, r) ./ N;
mean_Ip_g = boxfilter(I(:, :, 2).*p, r) ./ N;
mean_Ip_b = boxfilter(I(:, :, 3).*p, r) ./ N;

% covariance of (I, p) in each local patch.
cov_Ip_r = mean_Ip_r - mean_I_r .* mean_p;
cov_Ip_g = mean_Ip_g - mean_I_g .* mean_p;
cov_Ip_b = mean_Ip_b - mean_I_b .* mean_p;

% variance of I in each local patch: the matrix Sigma in Eqn (14).
% Note the variance in each local patch is a 3x3 symmetric matrix:
%           rr, rg, rb
%   Sigma = rg, gg, gb
%           rb, gb, bb
var_I_rr = boxfilter(I(:, :, 1).*I(:, :, 1), r) ./ N - mean_I_r .*  mean_I_r; 
var_I_rg = boxfilter(I(:, :, 1).*I(:, :, 2), r) ./ N - mean_I_r .*  mean_I_g; 
var_I_rb = boxfilter(I(:, :, 1).*I(:, :, 3), r) ./ N - mean_I_r .*  mean_I_b; 
var_I_gg = boxfilter(I(:, :, 2).*I(:, :, 2), r) ./ N - mean_I_g .*  mean_I_g; 
var_I_gb = boxfilter(I(:, :, 2).*I(:, :, 3), r) ./ N - mean_I_g .*  mean_I_b; 
var_I_bb = boxfilter(I(:, :, 3).*I(:, :, 3), r) ./ N - mean_I_b .*  mean_I_b; 

a = zeros(hei, wid, 3);
for y=1:hei
    for x=1:wid        
        Sigma = [var_I_rr(y, x), var_I_rg(y, x), var_I_rb(y, x);
            var_I_rg(y, x), var_I_gg(y, x), var_I_gb(y, x);
            var_I_rb(y, x), var_I_gb(y, x), var_I_bb(y, x)];
        %Sigma = Sigma + eps * eye(3);

        cov_Ip = [cov_Ip_r(y, x), cov_Ip_g(y, x), cov_Ip_b(y, x)];        

        a(y, x, :) = cov_Ip * inv(Sigma + eps * eye(3)); % Eqn. (14) in the paper;
    end
end

b = mean_p - a(:, :, 1) .* mean_I_r - a(:, :, 2) .* mean_I_g - a(:, :, 3) .* mean_I_b; % Eqn. (15) in the paper;

q = (boxfilter(a(:, :, 1), r).* I(:, :, 1)...
+ boxfilter(a(:, :, 2), r).* I(:, :, 2)...
+ boxfilter(a(:, :, 3), r).* I(:, :, 3)...
+ boxfilter(b, r)) ./ N;  % Eqn. (16) in the paper;
end

function imDst = boxfilter(imSrc, r)

%   BOXFILTER   O(1) time box filtering using cumulative sum
%
%   - Definition imDst(x, y)=sum(sum(imSrc(x-r:x+r,y-r:y+r)));
%   - Running time independent of r; 
%   - Equivalent to the function: colfilt(imSrc, [2*r+1, 2*r+1], 'sliding', @sum);
%   - But much faster.

[hei, wid] = size(imSrc);
imDst = zeros(size(imSrc));

%cumulative sum over Y axis
imCum = cumsum(imSrc, 1);
%difference over Y axis
imDst(1:r+1, :) = imCum(1+r:2*r+1, :);
imDst(r+2:hei-r, :) = imCum(2*r+2:hei, :) - imCum(1:hei-2*r-1, :);
imDst(hei-r+1:hei, :) = repmat(imCum(hei, :), [r, 1]) - imCum(hei-2*r:hei-r-1, :);

%cumulative sum over X axis
imCum = cumsum(imDst, 2);
%difference over Y axis
imDst(:, 1:r+1) = imCum(:, 1+r:2*r+1);
imDst(:, r+2:wid-r) = imCum(:, 2*r+2:wid) - imCum(:, 1:wid-2*r-1);
imDst(:, wid-r+1:wid) = repmat(imCum(:, wid), [1, r]) - imCum(:, wid-2*r:wid-r-1);

% imDst=colfilt(imSrc, [2*r+1, 2*r+1], 'sliding', @sum);
% imDst=colfilt(imSrc, [2*2+1, 2*2+1], 'sliding', @sum);
end

参考文献中[1]是adaptive weight立体匹配算法，[2]是加权中值滤波算法，[3]是导向滤波算法。[4]是box filter cost aggregation算法

5.参考文献
1.K. J. Yoon, I. S. Kweon. Locally Adaptive Support-Weight Approach for Visual Correspondence Search. CVPR. 2005.
2.Z. Ma, K. He, W. Y. Wei. Constant Time Weighted Median Filtering for Stereo Matching and Beyond. IEEE International Conference on Computer Vision. 2013.
3.K. He, J. Sun, X. Tang. Guided Image Filtering. ECCV. 2010.
4.D. Scharstein and R. Szeliski. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. IJCV,
pages 7–42, 2002.