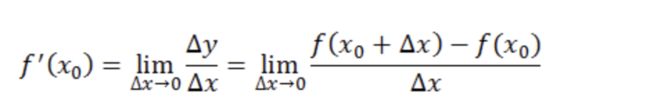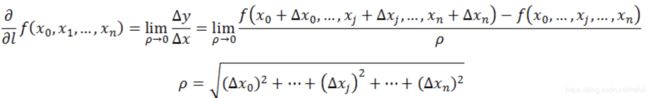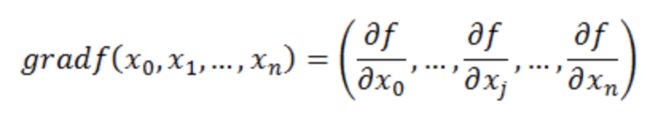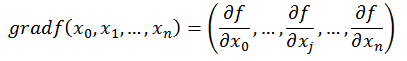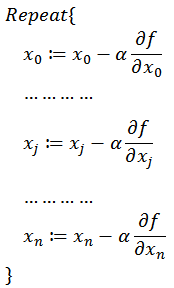通俗理解-梯度下降法(一)- 数学基础
什么是梯度下降
梯度下降法(gradient descent)是一种常见的一阶(first-order)优化方法,是求解无约束优化问题最简单、最经典的方法之一。所谓的一阶方法就是仅使用目标函数的一阶导数,不利用其高阶导数。
那什么是无约束优化问题呢?举个例子,在一元函数法f(x)的图像中,求无约束最优化问题,即不对定义域或值域做任何限制的情况下,求解函数f(x)的最小值。 没有理解,没事儿,本文最后会重新探讨这个问题。
梯度下降方法的重点是理解,导数(derivative)、偏导数(partial derivative)和方向导数(directional derivative)这三个概念。
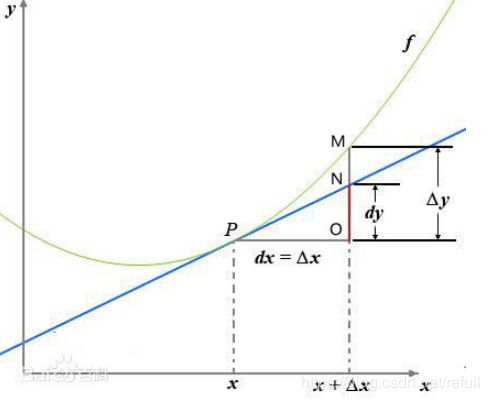
回忆一下高数中微积分的经典图片:
我们定义一下导数:
dx:x的变化量趋于0时,则记作微元dx。
Δy:Δy=f(x0+Δx)-f(x0),是函数的增量;
dy:dy=f’(x0)dx,是切线的增量;
其中,dy/dx中的d是微小增量的意思,即微小的增量y处以微小增量x,在函数中是微分的意思。也就是y=f(x)在x0处的斜率。
当Δx→0时,dy与Δy都是无穷小,dy是Δy的主部,即Δy=dy+o(Δx).
导数反应的是函数y=f(x)在从x轴某一点处沿着x轴正方向上的变化率或变化趋势。举个例子,在x轴某一点处,如果f’(x)>0,说明f(x)的函数值在x点沿x轴正方向是趋于增加的;反之,如果f’(x)<0,说明f(x)的函数值在x点沿x轴正方向是趋于减小的。
再来看偏导数的定义:
导数与偏导数本质是一致的,都是当自变量的变化量趋于0时,函数值的变化量与自变量变化量比值的极限。直观地说,偏导数也就是函数在某一点上沿坐标轴正方向的的变化率。
偏导数 f'x(x0,y0) 表示固定面上一点对 x 轴的切线斜率;偏导数 f'y(x0,y0) 表示固定面上一点对 y 轴的切线斜率。
高阶偏导数:如果二元函数 z=f(x,y) 的偏导数 f'x(x,y) 与 f'y(x,y) 仍然可导,那么这两个偏导函数的偏导数称为 z=f(x,y) 的二阶偏导数。二元函数的二阶偏导数有四个:f"xx,f"xy,f"yx,f"yy。
x方向的偏导
设有二元函数 z=f(x,y) ,点(x0,y0)是其定义域D 内一点。把 y 固定在 y0而让 x 在 x0 有增量 △x ,相应地函数 z=f(x,y) 有增量(称为对 x 的偏增量)△z=f(x0+△x,y0)-f(x0,y0)。
如果 △z 与 △x 之比当 △x→0 时的极限存在,那么此极限值称为函数 z=f(x,y) 在 (x0,y0)处对 x 的偏导数,记作 f'x(x0,y0)或。函数 z=f(x,y) 在(x0,y0)处对 x 的偏导数,实际上就是把 y 固定在 y0看成常数后,一元函数z=f(x,y0)在 x0处的导数。
y方向的偏导同理。
接下来是方向导数的定义:
当我们讨论函数沿任意方向的变化率时,也就引出了方向导数的定义,即:某一点在某一趋近方向上的导数值。
通俗的解释是:
我们不仅要知道函数在坐标轴正方向上的变化率(即偏导数),而且还要设法求得函数在其他特定方向上的变化率。而方向导数就是函数在其他特定方向上的变化率。
导数与梯度
梯度的定义如下:
梯度的提出只为回答一个问题:
函数在变量空间的某一点处,沿着哪一个方向有最大的变化率?
梯度定义如下:
函数在某一点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
这里注意三点:
1)梯度是一个向量,即有方向有大小;
2)梯度的方向是最大方向导数的方向;
3)梯度的值是最大方向导数的值。
导数与向量:
向量的定义是有方向(direction)有大小(magnitude)的量。
从前面的定义可以这样看出,偏导数和方向导数表达的是函数在某一点沿某一方向的变化率,也是具有方向和大小的。因此从这个角度来理解,我们也可以把偏导数和方向导数看作是一个向量,向量的方向就是变化率的方向,向量的模,就是变化率的大小。
从这个角度看,
梯度也就是函数在某一点最大的方向导数,函数沿梯度方向函数有最大的变化率。
最后我们回到梯度下降法:
既然在变量空间的某一点处,函数沿梯度方向具有最大的变化率,那么在优化目标函数的时候,自然是沿着负梯度方向去减小函数值,以此达到我们的优化目标。
如何沿着负梯度方向减小函数值呢?既然梯度是偏导数的集合,如下:
同时梯度和偏导数都是向量,那么参考向量运算法则,我们在每个变量轴上减小对应变量值即可,梯度下降法可以描述如下
以上是梯度下降法的一种理解方式,当然,也可以通过泰勒公式对目标函数进行展开推倒得到。
我们回到最开始的地方,为什么会有梯度下降法? 梯度下降其实是求解无约束最优化问题的一种常用方法,那么什么是无约束最优化问题,以及还有哪些其他方法可以解决这一问题呢? 这些问题另起一篇文章解读。
接下来,会做一些梯度下降的代码测试。