数据挖掘作业三：主成分分析、推荐系统和关联规则

中山大学软件工程数据挖掘第三次作业

---

github地址：https://github.com/linjiafengyang/DataMining

主成分分析（Principal Component Analysis，PCA）

请从课程网站或此链接下载Yale人脸数据集进行降维。通过MATLAB命令load(‘yale_face.mat’)读取数据，包含一个4096×165矩阵。（请注意，这里的矩阵X是课件第21页定义的数据矩阵X的转置。）此矩阵的每一列是由一张64×64灰度人脸图像所转成的向量。例如，可以使用imshow(reshape(X(:,1),[64 64]),[])命令显示第一张人脸图像（第一个训练样本）。

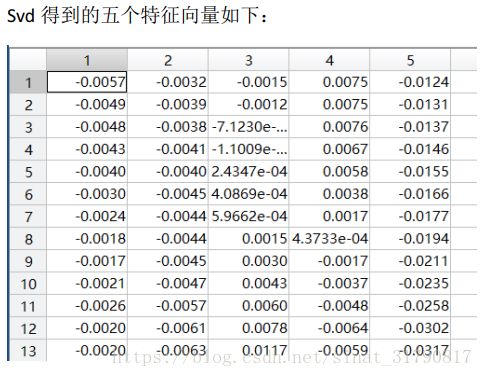
（1）试使用MATLAB中的svd函数实现PCA算法，即输入数据矩阵X和降维后的维数k，对每一个样本进行去中心化，然后对进行去中心化后的数据矩阵Xc用svd函数[U,S,V] = svd(Xc)，输出降维的投影矩阵Ureduce（即U的前k列），降维后的坐标表示Z=Ureduce’*Xc，训练样本均值μ。并令k=5，显示样本均值μ的图像和Ureduce的五个列向量（即协方差矩阵的前五个特征向量）所对应的图像；

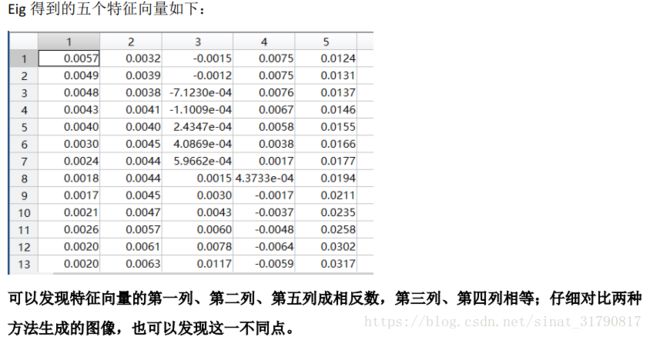
（2）试对协方差矩阵使用MATLAB中的eig函数计算特征值和特征向量，即[U,D]=eig(Xc*Xc’/m)，显示前五个最大的特征向量所对应的图像，并比较对数据矩阵使用svd函数的所得出的特征向量的图像与运算时间；

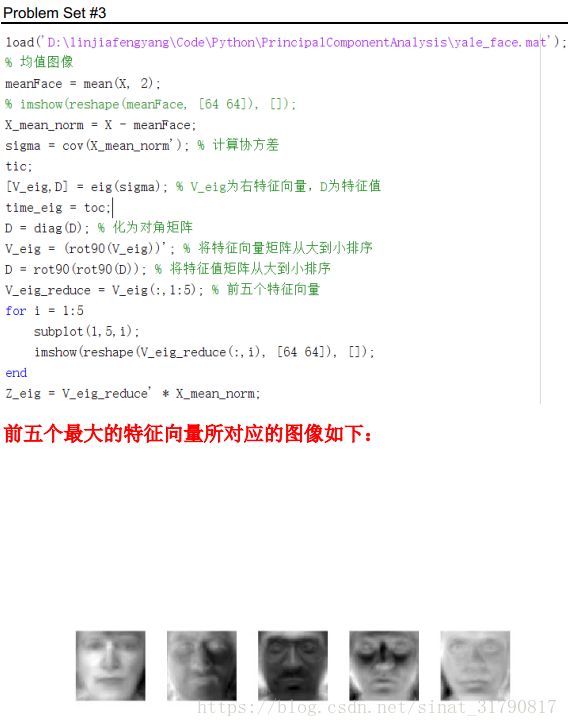
（3）试计算当降维后的维数分别是10和100时，保留的方差的比例，并分别利用10维和100维坐标恢复原高维空间中的人脸图像，对前三张人脸图像，对比原图和两张恢复的图像。

推荐系统（Recommender System）

考虑以下的8个用户（A-H）对7部电影评级（1到5级）的一个效用矩阵：

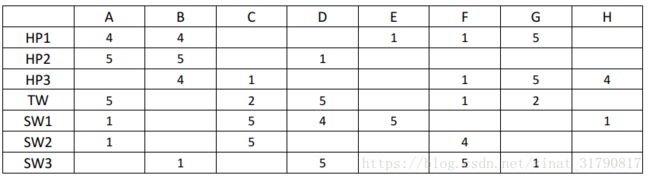
电影的名字HP1、HP2、HP3分别代表《哈利波特》（Harry Potter）I、II、III，TW代表《暮光之城》（Twilight），SW1、SW2和SW3分别代表《星球大战》（Star Wars）I、II、III。

（1）试实现协同过滤算法（Collaborative filtering algorithm，课件第19页，不需要进行去均值操作），令正则化参数λ=0.1，特征向量维数n=4，学习率α=0.01，分别计算描述电影特征的7×4矩阵X和预测用户评级的8×4模型参数矩阵Θ（定义见课件第23页，所得结果保留小数点后4位），并计算预测电影评级的7×8效用矩阵即XΘ^’（保留小数点后1位）；

答：协同过滤算法大致如下：

from scipy.io import loadmat
import numpy as np

def cost(X, Theta, Y, R, lamda, learning_rate, num_iterations):
    for i in range(0, num_iterations):
        # compute the cost
        error = np.multiply(np.dot(X, Theta.T) - Y, R)
        squared_error = np.power(error, 2)
        print("迭代次数 %d | 均方误差: %f" % (i+1, np.sum(squared_error)))
        J = (1 / 2) * np.sum(squared_error) + \
            ((lamda / 2) * np.sum(np.power(Theta, 2))) + \
            ((lamda / 2) * np.sum(np.power(X, 2)))
        # calculate the gradients with regularization
        X = X - learning_rate * ((error * Theta) + (lamda * X))
        Theta = Theta - learning_rate * ((error.T * X) + (lamda * Theta))
    return X, Theta

Y = np.matrix([[4, 4, 0, 0, 1, 1, 5, 0],
     [5, 5, 0, 1, 0, 0, 0, 0],
     [0, 4, 1, 0, 0, 1, 5, 4],
     [5, 0, 2, 5, 0, 1, 2, 0],
     [1, 0, 5, 4, 5, 0, 0, 1],
     [1, 0, 5, 0, 0, 4, 0, 0],
     [0, 1, 0, 5, 0, 5, 1, 0]])
R = np.where(Y == 0, Y, 1)

num_movies = Y.shape[0]
num_users = Y.shape[1]
num_features = 4

X = np.random.random((num_movies, num_features))
Theta = np.random.random((num_users, num_features))
X = np.ones((num_movies, num_features))
Theta = np.ones((num_users, num_features))

lamda = 0.1
learning_rate = 0.01
num_iterations = 23000

X, Theta = cost(X, Theta, Y, R, lamda, learning_rate, num_iterations)
print("X为:\n", np.around(X, decimals=4))
print("Theta为:\n", np.around(Theta, decimals=4))
result = np.dot(X, Theta.T)
result = np.around(result, decimals=1)
print("效用矩阵为:\n", result)

迭代多次基本达到收敛后：
下面结果不是固定的（因此我就省略了），因为参数随机初始化是不相同的，但最后得到的结果应该差不多。
特征矩阵X如下（保留小数点后四位）：略
参数矩阵Theta如下（保留小数点后四位）：略
效用矩阵XΘ^’如下（保留小数点后一位）：略

（2）试计算（1）中预测的电影评级与真实评级的平方误差；讨论哪两部电影和HP1最相似，哪两部电影和和SW1最相似；

答：运行（1）中给出的代码可得均方误差大致如下：略
根据（1）中得到的效用矩阵可知，HP2、HP3和HP1最相似，SW2、SW3和SW1最相似。因为每个用户对相似的电影的评级会很接近，即是说用户如果喜欢一部电影，那么他也会喜欢类似的电影；用户如果不喜欢一部电影，那么他也不会对类似的电影感兴趣。而效用矩阵很好地诠释了这一特点。

（3）试使用一个非零常数对协同过滤算法中的变量x^((1) ),…,x^((n_m ) ),θ^((1) ),…,θ^((n_u ) )进行初始化（即更改课件第19页Collaborative filtering algorithm的第一步为x^((1) )=⋯=x^((n_m ) )=θ^((1) )=⋯=θ^((n_u ) )=c1，其中c为非零实数，1为所有元素都是1的n=4维列向量；使用（1）中相同的参数，分别计算描述电影特征的7×4矩阵X和预测用户评级的8×4模型参数矩阵Θ（所得结果保留小数点后4位），并计算预测电影评级的7×8效用矩阵即XΘ^’（保留小数点后1位）和预测的电影评级与真实评级的平方误差；与（1）和（2）中的结果比较，讨论此初始化方法的问题。

答：假设我们初始化X为所有元素都为1的7×4矩阵，Theta为所有元素都为1的8×4矩阵，同样执行协同过滤算法，结果如下：
特征矩阵X如下（保留小数点后四位）：略
参数矩阵Theta如下（保留小数点后四位）：略
效用矩阵XΘ^’如下（保留小数点后一位）：略

与（1）（2）中的结果比较，可以发现将参数初始化为同一个参数会导致严重的问题，算法的效果非常差。随机初始化可以打破对称性，这和神经网络参数随机初始化的原因相似，随机初始化可以确保特征矩阵X和参数矩阵Theta在算法执行中保持不相同，而如果初始化为同一个参数在算法学习中难以达到梯度下降的优化效果，所以应避免这样的初始化。

关联规则

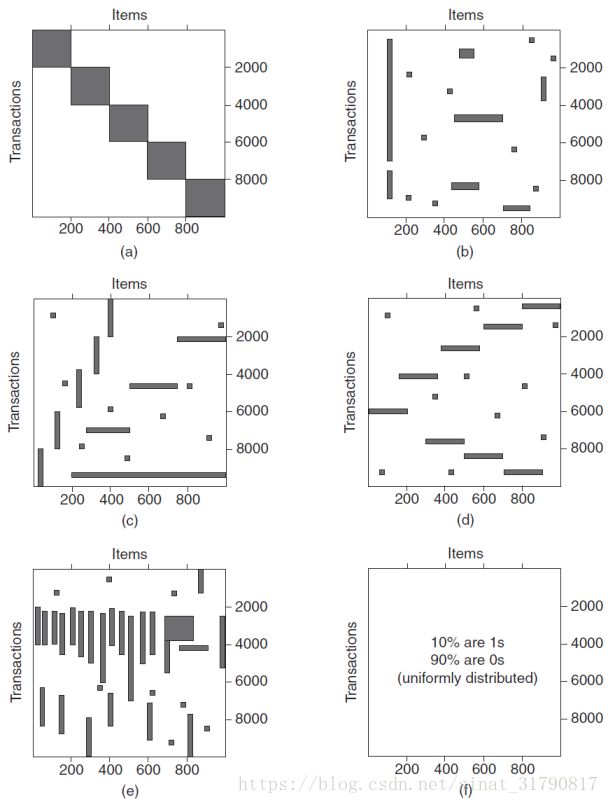
上面六个图（a）到（f）中的每一个图包含1000个商品和10000个交易的记录。灰色位置表示存在商品交易，而白色表示不存在商品交易。我们使用Apriori算法提取频繁项集，并设定频繁项集的最小支持度为10%，即minsup=10%（即频繁项集包含在至少1000个交易中）。根据上图回答以下问题：

（1）哪一个或几个数据集的频繁项集数目最多？哪一个或几个数据集的频繁项集数目最少？

答：a数据集的频繁项集数目最多，d数据集的频繁项集数目最少。

（2）哪一个或几个数据集的频繁项集长度最长（即包含最多商品）？

答：a数据集的频繁项集长度最长，包含最多商品。

（3）哪一个或几个数据集的频繁项集有最高的最大支持度（highest maximum support）？

答：b数据集的频繁项集有最高的最大支持度（highest maximum support）。

（4）哪一个或几个数据集的频繁项集有最大的支持度范围（例如频繁项集的支持度范围可以从小于20%变化到大于70%）？

答：b数据集的频繁项集有最大的支持度范围。