牛客网刷题汇总(一)附解析
纯虚函数是在基类声明的虚函数,它在基类中没有定义,但是要求派生类都要定义自己的实现方法。在基类中实现纯虚函数的方法是在函数原型后面添加“=0”,比如 virtual void f()=0;而C++中包含纯虚函数的类称为抽象类,由于抽象类中包含了没有定义的纯虚函数,所以不能定义抽象类的对象。
总结:
1.抽象类只能用作其他类的基类,不能定义抽象类的对象。
2.抽象类不能用于参数类型、函数返回值或显示转换的类型
3.抽象类可以定义抽象类的指针和引用,此指针可以指向它的派生类,进而实现多态性。
答案选C,通道方式。
(1)程序直接访问方式跟循环检测IO方式,应该是一个意思吧,是最古老的方式。CPU和IO串行,每读一个字节(或字),CPU都需要不断检测状态寄存器的busy标志,当busy=1时,表示IO还没完成;当busy=0时,表示IO完成。此时读取一个字的过程才结束,接着读取下一个字。
(2)中断控制方式:循环检测先进些,IO设备和CPU可以并行工作,只有在开始IO和结束IO时,才需要CPU。但每次只能读取一个字。
(3)DMA方式:Direct Memory Access,直接存储器访问,比中断先进的地方是每次可以读取一个块,而不是一个字。
(4)通道方式:比DMA先进的地方是,每次可以处理多个块,而不只是一个块。
union:当多个数据需要共享内存或者多个数据每次只取其一时,可以利用联合体(union);
它有以下特点:
(1)它是一个结构;
(2)它的所有成员相对于基地址的偏移量都为0;
(3)此结构空间要大到足够容纳最”宽”的成员;
(4)其对齐方式要适合其中所有的成员
综上:
而分配给union的实际大小不仅要满足是对齐大小的整数倍,同时要满足实际大小不能小于最大成员的大小。
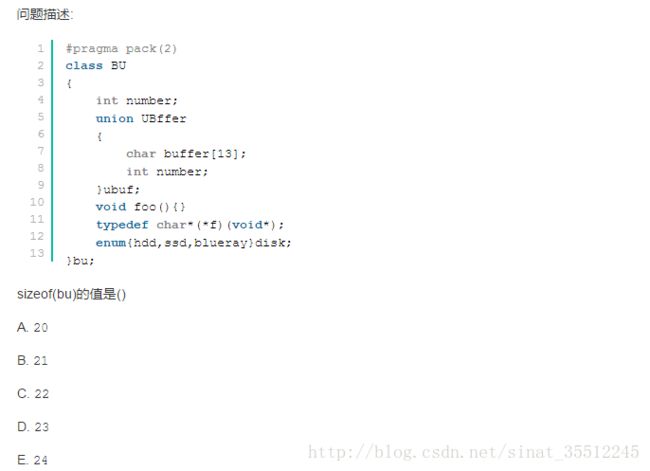
本题目中,注意第一行,#pragma pack(2);首先考虑没有这句话时,我们在类、结构或者union补齐字节的时候,找它们的成员数据中找字节最大的那个数去衡量如何对齐,假设为z; 但是有了这句话以后,对齐方式是取 pack(n)中n和z的最小值去对齐;可见本题中对齐字节数为2;之后往下看 int number; 占4个字节接下来考虑union大小:
union UBffer
{
char buffer[13]; // 13
int number; // 4
}ubuf; buffer 是13个字节,number 是4个字节,取最大的 为13,注意还要字节对齐,对齐字节数为2,所以Union大小为14,既满足buffer的对齐 也满足number的对齐。
void foo(){} 不占
typedef char*(f)(void); typedef char*(f)(void); 这个是定义类型,不占用空间。
enum{hdd,ssd,blueray}disk; 4个字节
综上,总大小为14+4+0+0 +4=22。
无影响的情况就是时间复杂度在最好的情况与最坏的情况下是不同的。如此,只有堆排序和归并排序是无影响的。
根据各种排序算法的流程,对于插入排序,如果几乎有序的话,每个节点的初始位置就最终位置,所以几乎不需要移动节点;
对于冒泡排序,如果节点几乎有序的话,对于一次遍历设置标记为,如果不交换元素的话即结束排序过程;
对于快速排序,如果以初始序列是逆序的话,时间复杂度变为 n2 ;
综上,时间堆排序的最差和最优时间复杂度都为nlgn,所以堆排序是最优的。
答案:A
解释:
B 默认的赋值运算符实现了“浅层复制”功能
C 重载的赋值运算符函数有一个本类对象作为形参
D 复制构造函数 和赋值构造函数 可以同时存在。
不能被重载的运算符: :: ,* . ?:
必须作为成员函数重载的运算符: = [] () ->
extern “C” 包含双重含义,从字面上即可得到:首先,被它修饰的目标是“extern”的;其次,被它修饰的目标是“C”的。
(1) 被extern “C”限定的函数或变量是extern类型的
extern是C/C++语言中表明函数和全局变量作用范围(可见性)的关键字,该关键字告诉编译器,其声明的函数和变量可以在本模块或其它模块中使用。记住,下列语句:
extern int a;
仅仅是一个变量的声明,其并不是在定义变量a,并未为a分配内存空间。变量a在所有模块中作为一种全局变量只能被定义一次,否则会出现连接错误。
通常,在模块的头文件中对本模块提供给其它模块引用的函数和全局变量以关键字extern声明。例如,如果模块B欲引用该模块A中定义的全局变量和函数时只需包含模块A的头文件即可。这样,模块B中调用模块A中的函数时,在编译阶段,模块B虽然找不到该函数,但是并不会报错;它会在连接阶段中从模块A编译生成的目标代码中找到此函数。
与extern对应的关键字是static,被它修饰的全局变量和函数只能在本模块中使用。因此,一个函数或变量只可能被本模块使用时,其不可能被extern “C”修饰。
(2) 被extern “C”修饰的变量和函数是按照C语言方式编译和连接的。
某计算机存储器按字节编址,采用小端方式存放数据。假定编译器规定int型和short型长度分别为32位和16位并且数据按边界对齐存储。某C语言程序段如下:
struct{
int a;
char b;
short c;
}
record;
record.a=273;若record变量的首地址为0XC008,则低地址0XC008中内容及record.c的地址是 ( B )
A. 0X00、0XC00D
B. 0X11、0XC00E
C. 0X11、0XC00D
D. 0X00、0XC00E
由于273的十六进制是0x00000111,所以小端存储,是按照11 10 00 00的顺序,那么第一个字节存的就是0x11。又因为边界对齐,a占4个字节,b占一个字节,c占两个字节,所以应该在b之后补1个空的字节,那么这样从a的第一个地址到的第一个地址需要增加6个字节,c的第一个地址便是0xC00E。
A、B、C、D、E 五个人捕鱼后已凌晨,大家便睡觉。早上A第一个醒来,将鱼均分成五份,把多余的一条鱼扔掉,拿走自己的一份,B第二个醒来,也将鱼均分为五份,把多余的一条鱼扔掉,拿走自己的一份。CDE依次醒来,也按同样的方法拿鱼,问他们合伙至少捕了几条鱼?(C)
A. 9
B. 31
C. 3121
D. 3906
假如我们多给4条鱼的话,那么就正好都够分的了 假如多给4条鱼之后鱼的数量为x;那么 A拿走后剩下 x*4/5 B拿走后剩下 x*4/5*4/5 …… E拿走后剩下 x*4/5*4/5*4/5*4/5*4/5=x*10244/3125 由于最后剩下的 的数量一定为整数所以鱼的数量为 3125-4=3121条。
哈夫曼树中,所有的字符串结点都是和其他字符串结点或者权值结点构成子树,因此不可能存在度为1的结点。
完全二叉树意为前n-1层为满二叉树,最后一层连续缺失右边结点的二叉树,而哈夫曼树无法保证最后一层连续缺失右边结点以及前n-1层为满二叉树。
树中任意节点的权值一定大于自己的左右孩子,但不能保证一定不小于其他下一任结点的权值。
生成哈夫曼树的第一步就是在结点集合中找到两个权值最小的结点,然后生成一棵二叉树。
IP数据报头采用()字节序,在此字节序下从低地址到高地址0x1234的表示形式为 (C) 。
A.big_endian,0x12 0x34 0 0
B.little_endian,0x34 0x12 0 0
C.big_endian,0 0 0x12 0x34
D.little_endian, 0 0 0x34 0x12
其实 big endian 是指低地址存放最高有效字节( MSB ),而 little endian 则是低地址存放最低有效字节( LSB )。 所有网络协议也都是采用 big endian 的方式来传输数据的。所以有时我们也会把 big endian 方式称之为网络字节序。当两台采用不同字节序的主机通信时,在发送数据之前都必须经过字节序的转换成为网络字节序后再进行传输。
比如数字 0x12345678 在两种不同字节序 CPU 中的存储顺序如下所示:
Big Endian
低地址 高地址
—————————————–>
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
| 12 | 34 | 56 | 78 |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
Little Endian
低地址 高地址
—————————————–>
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
| 78 | 56 | 34 | 12 |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
struct T {
char a;
int *d;
int b;
int c:16;
double e;
};
T *p;在64位系统以及64位编译器下,以下描述正确的是(C)
A.sizeof(p) == 24
B.sizeof(*p) == 24
C.sizeof(p->a) == 1
D.sizeof(p->e) == 4
sizeof(p) == 8 P为指针,64位系统地址占8个字节
sizeof(*p) == 24 根据内存对齐
sizeof(p->a) == 1 正确
sizeof(p->e) == 8 double
小数值1.5625的二进制表示是?( D )
A.101.1001
B.0.001
C.101.111
D.1.1001
小数点左侧:1 二进制还是1
右侧为.5625
采用乘2取整法
.5625*2 = 1.125………………..1
.125*2 = 0.25 …………………0
.25*2 = 0.5……………………0
.5*2 = 1.0……………………1
所以 答案为1.1001
设一棵二叉树中有3个叶子节点,有8个度为1的节点,则该二叉树中总的节点数为?
有公式:N2=N0-1,度为2的节点个数是度为0的节点个数减一,所以N0=3,则N2=2,再加上N1=8,总的是13
找不到该页面:404
禁止访问:403
内部服务器访问:500
服务器繁忙:503
http1.1状态吗分为五类
100-199 指定客服端相应的某些动作
200-299 表示请求成功
300-399 用于已经移动的文件并且包含在定位头信息中指定
400-499 客服端错误
500-599 服务端错误
线程共享的内容包括:
1.进程代码段
2.进程的公有数据(利用这些共享的数据,线程很容易的实现相互之间的通讯)
3.进程打开的文件描述符、
4.信号的处理器、
5.进程的当前目录和
6.进程用户ID与进程组ID
线程独有的内容包括:
1.线程ID
2.寄存器组的值
3.线程的堆栈
4.错误返回码
5.线程的信号屏蔽码
设计模式分为三种类型,共23种。
创建型模式:单例模式、抽象工厂模式、建造者模式、工厂模式、原型模式。
结构型模式:适配器模式、桥接模式、装饰模式、组合模式、外观模式、享元模式、代理模式。
行为型模式:模版方法模式、命令模式、迭代器模式、观察者模式、中介者模式、备忘录模式、解释器模式、状态模式、策略模式、职责链模式、访问者模式。
二路归并:如果序列中有n 个记录,可以先把它看成n个子序列,每个子序列中只包含一个记录,因而都是排好序的。二路归并排序先将
每相邻的两个子序列合并,得到n/2(向上取整)个较大的有序子序列,每个子序列包含2个记录。再将这些子序列两两合并。如此反复,
直到最后合并成一个有序序列,排序即告完成。
设有数列{6,202,100,301,38,8,1}
初始状态:6,202,100,301,38,8,1
第一次归并后:{6,202},{100,301},{8,38},{1},比较次数:3;
第二次归并后:{6,100,202,301},{1,8,38},比较次数:4;
第三次归并后:{1,6,8,38,100,202,301},比较次数:4;
总的比较次数为:3+4+4=11;
关键码序列(Q,H,C,Y,Q,A,M,S,R,D,F,X),要按照关键码值递增的次序进行排序,若采用初始步长为4的Shell的排序法,则一趟扫描的结果是 () ;若采用以第一个元素为分界元素的快速排序法,则扫描一趟的结果是 () 。
参考答案 QACSQDFXRHMY
参考答案 FHCDQAMQRSYX
希尔排序,步长默认先从数组长度的一般开始,然后每次减半,直到最后为1。
题目所给为4,因此,上来1,5,9号元素(即QQR)进行比较,在这三个位置上进行排序,即还是QQR;
然后2,6,10号元素(即HAD)进行比较,在这三个位置上进行排序,即变成了ADH
依次排序后面的,即可获得QACSQDFXRHMY。
表达式a+b*c-(d+e)/f的后缀表达式为()
abc*+de+f/-
a+b*c-(d+e)/f –> a+b*c-(de+)/f –> a+(bc*)-(de+f/) –>(abc*+)-(de+f/) –>abc*+de+f/-
自动数据类型转换
自动转换按从低到高的顺序转换。不同类型数据间的优先关系如下:
低 ———————————————> 高
byte,short,char-> int -> long -> float -> double
C++中:
重载前缀++: operator++();表达式++a,运用成员函数调用方式为:a.operator++()
重载后缀++: operator++(int); 表达式a++,运用成员函数调用方式为:a.operator++(1)
40亿个非负整数中找到出现两次的数和所有数的中位数
对于在很多整数中找出现次数的题,一般是使用哈希表对出现的每一个数做词频统计的。但是这个题只需要找出现2次的整数,如果还使用哈希表 key表示出现的数,value表示出现的数的次数,那么这样需要的内存空间更大,而且对于出现次数大于2次的数没必要再去统计,所以哈希表在此处有点不太合适。那么应该怎么计算呢,我们先计算一下,如果每一个数用2位来做词频统计,那么就包括了0次是00,1次是01,2次是10,3次是11,这样就足够了,也省下不少空间,一个数2位,40亿个数就是80亿位,也就是10亿字节,那么就需要大概1GB的空间来处理,刚好满足条件。
具体计算步骤如下:
1、申请开辟一个长度为4294967295*2的bit数组,即bitArray[4294967295*2],占用内存空间约为1GB。
2、用bitArray数组的每2个位置表示一个出现的词频,遍历40亿个数,记为num,如果第一次出现num,则把
bitArray[num*2]和bitArray[num*2+1]置为01,num第二次出现就把bitArray[num*2]和bitArray[num*2+1]设
置为10,第三次出现就设置为11,如果大于3次出现则忽略不管,仍然保持11状态。
3、遍历bitArray数组,如果发现bitArray[i*2]和bitArray[i*2+1]的值是10,那么i就是出现了两次的数。
- char、short、int、long、bool 基本类型都可以用于switch语句。
- float、double都不能用于switch语句。
- enum类型,即枚举类型可以用于switch语句。
- 所有类型的对象都不能用于switch语句。
- 字符串也不能用于switch语句
类初始化对象其运行的先后顺序为:父类中的静态成员变量、父类中的静态块、父类中的静态方法、子类中的静态成员变量、子类中的静态块、子类中的静态方法、父类的构造器、父类中的普通成员变量、父类中的普通方法、子类构造器、子类普通成员变量、子类中的普通方法。父类的构造器实际是通过super()套用在子类的构造器之中。
堆栈是一个在计算机科学中经常使用的抽象数据类型。堆栈中的物体具有一个特性: 最后一个放入堆栈中的物体总是被最先拿出来, 这个特性通常称为后进先出(LIFO)队列。 堆栈中定义了一些操作。 两个最重要的是PUSH和POP。 PUSH操作在堆栈的顶部加入一 个元素。POP操作相反, 在堆栈顶部移去一个元素, 并将堆栈的大小减一。
1.没有回收垃圾资源
2.层次太深的递归调用
设置虚函数须注意:
1:只有类的成员函数才能说明为虚函数;
2:静态成员函数不能是虚函数;
3:内联函数不能为虚函数;
4:构造函数不能是虚函数;
5:析构函数可以是虚函数,而且通常声明为虚函数。
已知rand7()可以产生1~7的7个数(均匀概率),利用rand7() 产 生 rand10() 1~10(均匀概率)。
int rand10() {
int temp1;
int temp2;
do
{
temp1 = rand7();
}while(temp1>5);
do {
temp2 = rand7(); }
while(temp2>2);
return temp1+5*(temp2-1);
}
定理: 给定生成随机1~n的随机函数,利用公式: n* ( f(n) - 1 ) + f ( n) 生成的 1 ~ n * n 的 随机数是均匀的;
5 * ( rand5() -1 ) + rand5() 获得的是 1 - 25 之间的随机数,去掉21之后的数,就是1~21 之间均匀随机的数,再/3就是1~7之间的数。
生成随机7的函数如下:
int rand7()
{
for ( ; ; )
{
int iRand = 5 * ( rand5() - 1 ) + rand5();
if ( iRand > 21 )
{
continue;
}
return iRand / 3;
}
}
数学相关
假设集合A,以及基于A上的关系R有如下性质:
自反: 如果a是A的元素,那么(a,a)是R的元素
反自反: 如果a是A的元素,那么(a,a)不是R的元素
对称:如果(a,b)是R的元素,那么(b,a)是R的元素
反对称:如果(a,b),(b,a)是R的元素,那么a,b相等
传递:如果(a,b),(b,c)是R的元素,那么(a,c)是R的元素
S市A,B共有两个区,人口比例为3:5,据历史统计A的犯罪率为0.01%,B区为0.015%,现有一起新案件发生在S市,那么案件发生
在A区的可能性有多大?()
解析:犯罪率可以理解为AB两区的犯罪人数与总人口数的比。由此不难列出下式:
( 3*0.01% ) / ( 3*0.01% + 5*0.015% ) = 28.6%
答案:C
严格的数学解析过程如下:(C表示犯案属性)
在A区犯案概率:P(C|A)=0.01%
在B区犯案概率:P(C|B)=0.015%
在A区概率:P(A)=3/8
在B区概率:P(B)=5/8
犯案概率:P(C)=(3/8*0.01%+5/8*0.015%)
则犯案且在A区的概率:P(A|C)=P(C|A)P(A)/P(C)=0.01%(3/8)/(3/8*0.01%+5/8*0.015%)≈28.6%