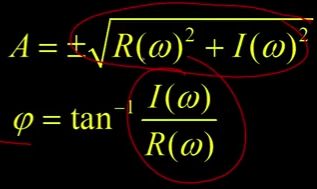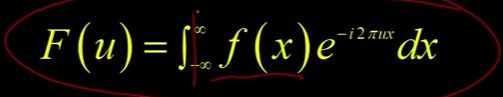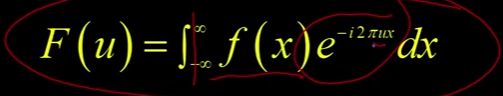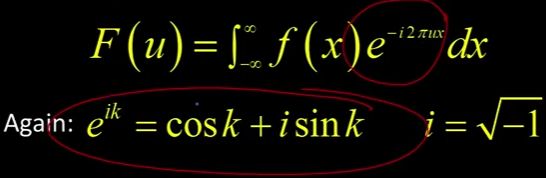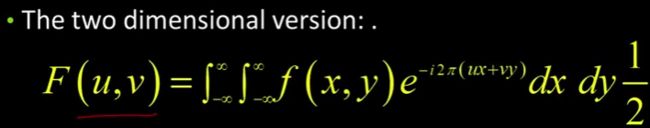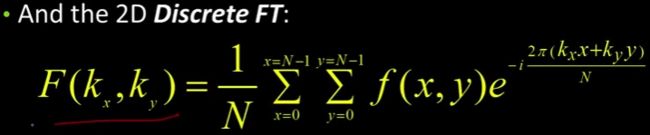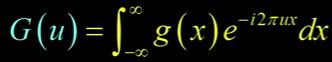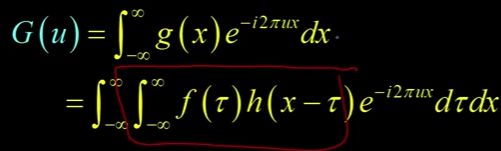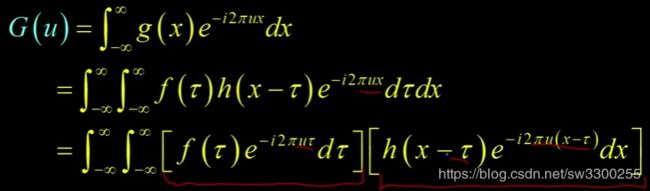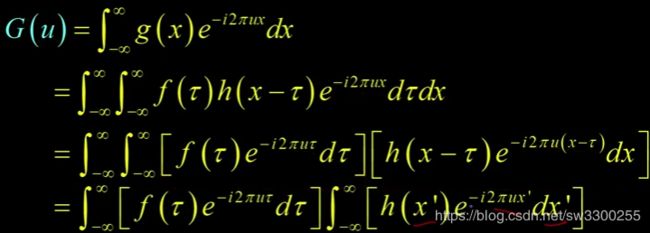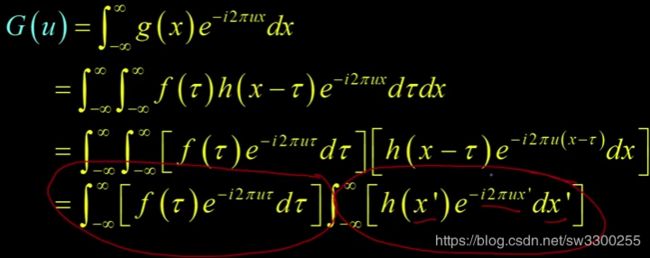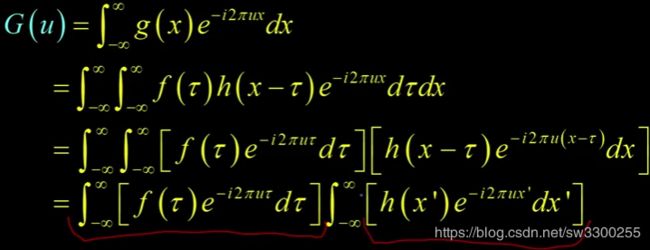11.频域里的卷积——介绍,傅里叶变换和卷积,快速傅里叶变换(FFT)_1
目录
介绍
傅里叶变换和卷积
FFT
介绍
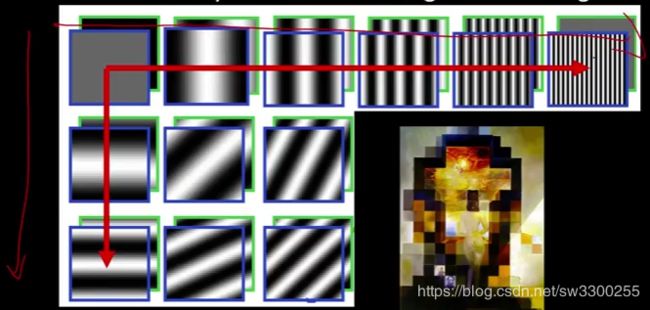
我们将继续讨论频率分析以及如何用频率分量的概念来研究图像。如果你还记得上次我们讲过的基于频率的图像分解的概念。我们通过给你们看这张照片来回忆它(如图)。这是著名的Dali图片,当你在那里允许高频图像时,你会看到一个女人在欣赏地中海之类的东西。
但是当你模糊它的时候,就是当你去掉高频的时候只有低频的时候,它就变成了林肯的照片。值得我们思考的是我们如何分解图像,思考什么是所涉及频率的基集,以及 基集将是一些函数,我们将线性地跨越我们可能的信号。所以我们的想法是我们应该从这个集合中建立并制造出任何可能的信号,并且它们是线性无关的,所以基本上我可以做这个求和。我们也会在模糊的基底集合中结束,所以当你改变一个基底元素的数量时,你不会得到其他元素的任何变化。
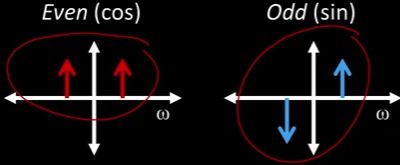
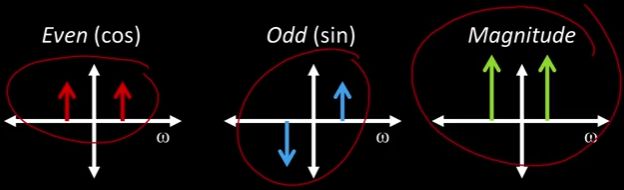
我们讨论的基集是这个傅里叶集(如图),对吧? 傅里叶集基本上把东西分解成正弦曲线,它们是频率不断增加的正弦曲线它们是垂直(如图垂直箭头)和水平移动(如图水平箭头)的,我们可以这样构造图像。
所以相关这个想法是我们称之为傅里叶变换的概念,而傅里叶变换就是你会输入一个信号,在这里以1D显示它,但也在2D中谈论它,你会得到的不是![]() 的函数(即位置函数的强度),你得到是一个F,作为
的函数(即位置函数的强度),你得到是一个F,作为![]() 的函数是频率。这个想法是,F可以分解成一个偶数分量和一个奇数分量用复数表示,这样我们就可以同时表示给定频率的大小
的函数是频率。这个想法是,F可以分解成一个偶数分量和一个奇数分量用复数表示,这样我们就可以同时表示给定频率的大小![]() 和 相位
和 相位![]()
![]() (如图)。
(如图)。
如果你想的话,你可以恢复大小和相位。大小就是每个实分量和虚分量平方和的平方根(如图),相位就是这个关系的arctan(反正切,如图)。
做傅里叶变换用这种难看的积分表示。这里我用1D向你们展示,我们会在2D中再做一次。但是你要做的是把函数从负无穷到正无穷进行积分(如图)。
你把它乘以任何频率的正弦曲线(如图),有时甚至是频率![]() 。当我们在二维空间中计算u和v时,这是它的形式。尽管这看起来不像正弦函数,
。当我们在二维空间中计算u和v时,这是它的形式。尽管这看起来不像正弦函数,
但你必须记住e的ik次方是cosk + isink。
这就是让我们从空间域到频域的原因。我们也提到过,如果你想的话,你可以逆这个(如图),对吧? 如果你给我一个信号的傅里叶变换f (u)从而改变它是正的还是负的,我可以做积分得到原始信号。
现在有u和v。
我们还讨论了离散型。我们在这里展示了一些例子你们用求和代替积分。
大多数时候,我们最感兴趣的是功率。还记得平方和的平方根吗?在这里表示出来。所以我可能有一个信号有一定的偶数部分和奇数部分,或者说是实部、虚部,
你用的平方和的平方根,得到平方和的大小(如图),当我们讨论任何给定图像的频率存在时,我们通常要讨论的是功率的大小。我们想知道它的功率。这个相位对重建很重要,但一般来说,我们不会做重建。
今天,我们要做的是,我们要把傅里叶变换和卷积联系起来。特别是,空间中的卷积是如何乘以频率的,我来给你们演示一下。
傅里叶变换和卷积
假设有一个函数 ![]() ,它就是
,它就是 ![]() 与
与 ![]() 的卷积(如图)。也许
的卷积(如图)。也许 ![]() 是一个滤波器,
是一个滤波器,![]() 是原始图像,没关系,它是
是原始图像,没关系,它是 ![]() 与
与 ![]() 的卷积,
的卷积,
假设我想要 ![]() 的傅里叶变换。这将被写成这样,我们的定义是,
的傅里叶变换。这将被写成这样,我们的定义是,![]() 就是
就是![]() 的傅里叶变换。
的傅里叶变换。
但是![]() 只是卷积,这是
只是卷积,这是 ![]() 和
和 ![]() 的卷积(如图)。记住这是
的卷积(如图)。记住这是 ![]() 的定义,
的定义,![]() 和
和 ![]() 的卷积。
的卷积。
我能做的是重新整理一下(如图),你们会看到我在这里做的是,第二个公式是 ![]() ,这里是
,这里是 ![]() ,这里是
,这里是 ![]() 。如果把它们相乘,就得到
。如果把它们相乘,就得到 ![]() ,这是一样的。但是我重新整理了一下后,所有的
,这是一样的。但是我重新整理了一下后,所有的 ![]() 都在这里。所有的
都在这里。所有的 ![]() 元素都在那里,这个
元素都在那里,这个 ![]() 在那里,
在那里,
所以,我们将快速改变变量,对吧?我要说,让我们定义一个 ![]() 是
是 ![]() 素数的新变量,现在我把它转换成x '(x prime),
素数的新变量,现在我把它转换成x '(x prime),
现在这里有一个积分,这里也有一个积分。如果你盯着这些,然后问自己,准备好。这些积分是什么?
我们来看看这个积分。这是 ![]() 的傅里叶变换,对吧? 这里用的是
的傅里叶变换,对吧? 这里用的是 ![]() 而不是
而不是 ![]() ,但这是一样的。另一个积分(公式的右边),这是
,但这是一样的。另一个积分(公式的右边),这是 ![]() 的傅里叶变换,
的傅里叶变换,
所以可以写成![]() *
*![]() ,所以
,所以 ![]() 等于
等于![]() 乘以
乘以![]() ,换句话说,记住
,换句话说,记住 ![]() 是
是 ![]() 和
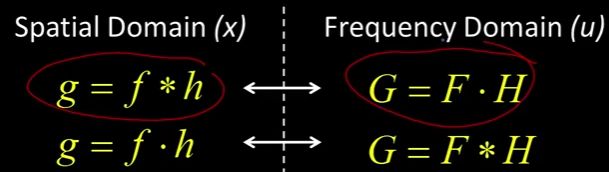
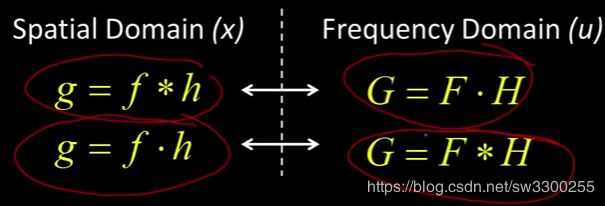
和 ![]() 的卷积。G (u)频域就是F和H的傅里叶变换的乘积,Okay? 所以,这里的思想是当你在空间域做卷积时,实际上是在频域做乘法。这是非常重要的,后面我们要讲混叠的时候,这也是我们要讲的卷积是如何进行频率操作的。
的卷积。G (u)频域就是F和H的傅里叶变换的乘积,Okay? 所以,这里的思想是当你在空间域做卷积时,实际上是在频域做乘法。这是非常重要的,后面我们要讲混叠的时候,这也是我们要讲的卷积是如何进行频率操作的。
这是写在这里的,如果在空间域中我做卷积,在频域中我做乘法。顺便说一下,由于变换的对称性。
如果我要在空间域中相乘,也就是说,如果我取两个函数并把它们相乘,我就不对它进行卷积,我只是将它们相乘(如图左2等式)。新函数的傅里叶变换将是每个函数的傅里叶变换的卷积(如图右2等式)。我们会用到它,在这里,当我们讨论混叠的时候。所以,在空间域中你做卷积,在频域中是乘法或者反之亦然。
FFT
这实际上意味着,这在不久前更为重要,但人们今天仍然使用它。如果我想用一些非常大的滤波器卷积函数,这通常是很昂贵的运算,实际上我可以用一种稍微不同的方法来做,这在这里显示出来了。假设我想要的,g 是 f 和 h 做卷积,假设 f 和 h 都是非常大的东西,所以你还记得卷积丑陋的原因是![]() ,其中N是图像的大小
,其中N是图像的大小 ![]() 和
和 ![]() ,所以我们能做的是,我们实际上可以采用 F的傅里叶变换 和 H的傅里叶变换。
,所以我们能做的是,我们实际上可以采用 F的傅里叶变换 和 H的傅里叶变换。
还有一种傅里叶变换的快速方法,叫做快速傅里叶变换(FFT),我们不会谈论关于FFT,但我可以快速完成那些傅里叶变换,然后我可以将这两个傅里叶变换相乘得到新的傅里叶变换, 那么我可以做逆傅里叶变换来得到答案(如图)。就像我说的那样,当机器速度较慢时,这非常重要,现在人们倾向于在空间领域工作,但即使在今天,如果你有一个大滤波器或一些你尝试对大图像进行卷积的大函数,使用傅里叶技巧来做到这一点并不罕见。
——学会编写自己的代码,才能练出真功夫。