初步认识ADRC(自抗扰控制)与应用
这是一个目录
- ADRC的基本原理
- 一、参考资料推荐
- 二、为什么PID好,以及,为什么PID不够好
- 1.为什么PID好——不依赖于模型的控制器
- 2.为什么PID不够好——PID的缺点
- 三、ADRC给出的方案——如何保留PID的优点,同时弥补PID的缺点
- 1. 误差的取法——安排过渡过程
- 2. 由误差提取误差微分的方法——跟踪微分器
- 3. 加权和的策略不一定最好——非线性反馈
- 4. 积分反馈的副作用——扩张状态观测器
- ADRC的公式以及参数整定
- 一、跟踪微分器(TD)
- 二、非线性反馈函数
- 三、扩张状态观测器(ESO)
- ADRC应用到二阶导弹模型
- matlab脚本
- simulink模型
- 结语
ADRC的基本原理
一、参考资料推荐
想要初步了解ADRC,可以从韩京清教授的一篇文献和一本书看起
1.文献: 从PID技术到“自抗扰控制”技术(《控制工程》,2002)
2.书: 自抗扰控制技术——估计补偿不确定因素的控制技术
不过文章里讲的不是很细,是把之前多篇文章内容综合到一起提出了ADRC整体的控制框架。想要更深入学习当然还是看书更好一些。
二、为什么PID好,以及,为什么PID不够好
1.为什么PID好——不依赖于模型的控制器
经典的PID控制直到如今都还是应用最广泛的控制算法,大部分的控制系统里用的都还是这个。它的好处主要在于,不需要被控对象的模型。
什么是被控对象的模型?
举个例子,假设我们以小车的速度 V V V为被控量,但是推动小车的力 F F F才是我们的控制量。
考虑阻力并假设阻力和速度成正比的话,根据牛顿第二定律我们可以得到小车的动力学方程 F − k V = m a F-kV=ma F−kV=ma,其中 k k k为阻力系数, m m m为小车质量。
根据质点运动学方程又有 V ˙ = a \dot{V}=a V˙=a,
这样就可以得到利用外力 F F F控制小车速度 V V V的模型 V ˙ = − k m V + 1 m F \dot{V}=-\frac{k}{m}V+\frac{1}{m}F V˙=−mkV+m1F
(也就是 x ˙ = − A x + B u \dot{x}=-Ax+Bu x˙=−Ax+Bu的线性模型的结构)
OK,这个方程通常就是我们需要的,如果要应用现代控制理论(比如最优控制)设计一个控制器,那么我们就需要知道这个模型的全部信息东西,在这里就是模型的结构以及阻力系数 k k k和小车质量 m m m。
获得这个模型存在两个问题:
- 实际工程的模型结构远比这复杂。比如阻力和速度的关系可能并不是成正比,我们只是这么假设的,实际的的关系可能是一个复杂的非线性函数。
- 模型的参数难以获得。这里的阻力系数 k k k和小车质量 m m m好像挺容易获得的,但是实际被控对象的模型参数可能要多的多,有些是很难获得的。
由于模型难获得,而现代控制理论又大多基于模型设计,虽然能够满足各种各样的性能条件,但大都不够实用,这也就导致了PID一直称霸各个控制领域。因为PID是只利用误差 e e e 来计算控制量的,不需要模型知识,只需要调一调 K P , K I , K D K_P,K_I,K_D KP,KI,KD 三个参数就能得到可以接受的效果。
2.为什么PID不够好——PID的缺点
注意到前面说 PID 能得到可以接受的效果,我们当然希望PID能够得到更好的控制效果,那么PID还有哪些不足呢?
以下摘自前面说的韩京清的那篇文章
- 误差的取法(直接由给定指令计算误差)
- 由误差提取误差微分的方法(使用传统的线性微分器)
- 加权和的策略不一定最好(比例,积分,微分项各乘上放大系数 K K K然后相加来计算控制量)
- 积分反馈有许多副作用(对误差进行积分并放大然后反馈到系统)
三、ADRC给出的方案——如何保留PID的优点,同时弥补PID的缺点
上一节写了PID的几个缺点,下面一条一条解释这些缺点的意思,并给出ADRC的解决方案:
1. 误差的取法——安排过渡过程
直接根据给定指令计算误差可能会导致控制效果变差,比如有些指令里包含了我们不希望的高频信号,这类信号的例子有:阶跃指令,方波指令。
为了将高频信号解决掉,ADRC提出了安排“过渡过程”的方法,类似于把给定指令进行低通滤波,得到一个更容易实现的指令,从而在牺牲一点快速性的同时大大降低超调。
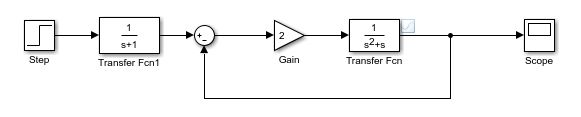
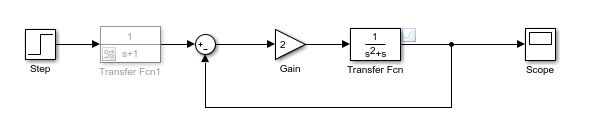
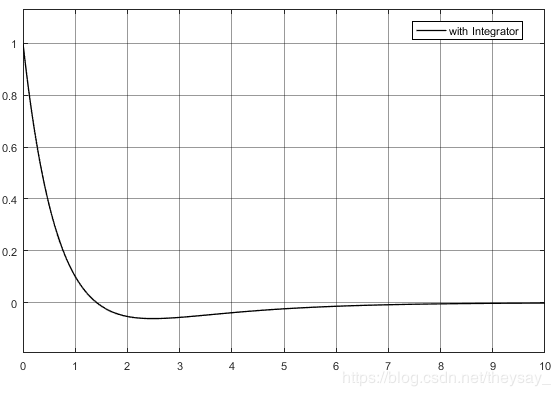
当指令为单位阶跃指令,只用一个增益 K = 2 K=2 K=2来控制二阶系统 1 s 2 + s \frac{1}{s^2+s} s2+s1的时候,有无指令滤波器的效果如下:
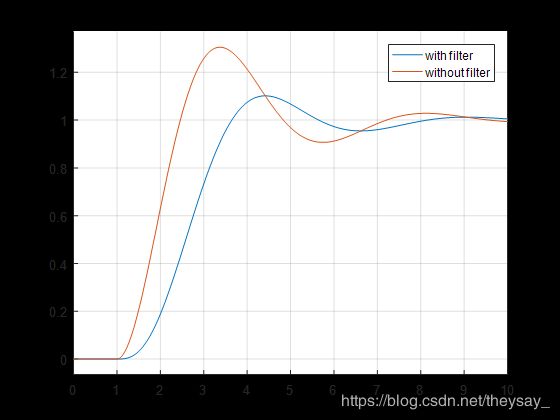
不难看到,加了指令滤波器之后,虽然上升速度变慢了,但是超调更小了,调节时间基本没变,甚至还缩短了。
安排过渡过程也是类似这样的道理。因为像阶跃这样变化太快的突变信号,当控制器增益高的话就很容易引起超调,如果提前安排过渡过程,让指令信号慢一点变化,就能得到更好一点的控制效果。
2. 由误差提取误差微分的方法——跟踪微分器
经典的线性微分器,如 W = s τ s + 1 W=\frac{s}{\tau{s}+1} W=τs+1s以及 W = s ∗ ω 2 s 2 + 2 ω s + ω 2 W=\frac{s*\omega^2}{{s}^2+2\omega{s}+\omega^2} W=s2+2ωs+ω2s∗ω2都是在跟踪给定信号的同时输出微分量。
这部分在韩京清的那本书上也有介绍,但是用公式解释可能比较枯燥,在simulink上画图就比较直观:
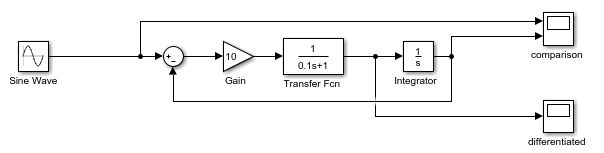
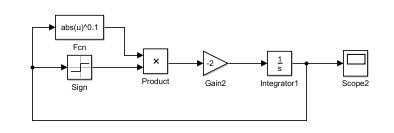
对于一阶线性微分器: W = s τ s + 1 W=\frac{s}{\tau{s}+1} W=τs+1s,其实可以看成是一个惯性环节的微分:
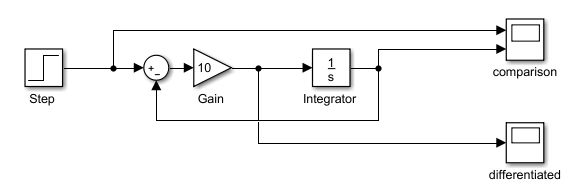
我们知道惯性环节 G = 1 τ s + 1 G=\frac{1}{\tau{s}+1} G=τs+11 是可以无超调的跟踪到给定阶跃信号的。当 G = 1 τ s + 1 G=\frac{1}{\tau{s}+1} G=τs+11 跟踪原信号的同时,积分器 1 s \frac{1}{s} s1 前面的量也就是 W = G ∗ s = s τ s + 1 W=G*s=\frac{s}{\tau{s}+1} W=G∗s=τs+1s 也在输出 G G G的微分量,那么我们就可以管这个叫做跟踪-微分器。它一边实现对原信号的跟踪,一边提供微分信号。
注意:当上图的Gain越大,也就是惯性环节的时间常数 τ \tau τ 越小的时候,惯性环节跟踪原信号就越快。对于输入信号为正弦波信号的情况就是相位滞后和幅值损失越小,这一点可以综合惯性环节的伯德图来思考。我们当然是希望相位滞后尽可能的小,但是 τ \tau τ 越大则 W = s τ s + 1 W=\frac{s}{\tau{s}+1} W=τs+1s 得到的微分信号对高频噪声的放大也越明显,这一点也可以综合微分环节 s s s 的伯德图来考虑。
类似的,二阶微分器 W = s ∗ ω 2 s 2 + 2 ω s + ω 2 W=\frac{s*\omega^2}{{s}^2+2\omega{s}+\omega^2} W=s2+2ωs+ω2s∗ω2 也可以看成一个阻尼比为1的震荡环节 G = ω 2 s 2 + 2 ω s + ω 2 G=\frac{\omega^2}{{s}^2+2\omega{s}+\omega^2} G=s2+2ωs+ω2ω2 的微分,即 W = G ∗ s W=G*s W=G∗s。
注意:这个二阶惯性环节,也可以看成一个闭环二阶系统跟踪指定的指令(这句话比较有意思)。公式如下:
{ x ˙ 1 = x 2 x ˙ 2 = u = − ω n 2 ( x 1 − x r e f ) − 2 ω n x 2 \left\{ \begin{array}{rcl} \dot{x}_1 &=& x_2 \\ \dot{x}_2 &=& u =-\omega_n^2(x_1-x_{ref})-2\omega_nx_2\\ \end{array} \right. {x˙1x˙2==x2u=−ωn2(x1−xref)−2ωnx2
其中 x r e f x_{ref} xref 为指定的指令。这个公式的形式和上面那个图虽然不是很像,但是实际上二者是等效的。
参考这个思想,可不可以用最速控制来实现这个二阶系统的指令跟踪,从而构造出一个新的跟踪-微分器?
ADRC的跟踪-微分器就是这么来的。
考虑一个二阶系统:
{ x ˙ 1 = x 2 x ˙ 2 = u ( ∣ u ∣ ≤ r ) \left\{ \begin{array}{rcl} \dot{x}_1 &=& x_2 \\ \dot{x}_2 &=& u &(|u|≤r)\\ \end{array} \right. {x˙1x˙2==x2u(∣u∣≤r)
则以原点为收敛点的最速控制函数为:
u = − r s i g n ( x 1 + x 1 ∣ x 2 ∣ 2 r ) u=-rsign(x_1+\frac{x_1|x_2|}{2r}) u=−rsign(x1+2rx1∣x2∣)
可以设计跟踪器为:
u = − r s i g n ( x 1 − x r e f + x 1 ∣ x 2 ∣ 2 r ) u=-rsign(x_1-x_{ref}+\frac{x_1|x_2|}{2r}) u=−rsign(x1−xref+2rx1∣x2∣)
这就是ADRC的跟踪-微分器的连续形式,但是这个东西在进入稳态后算出来的微分量会一直高频振荡。主要原因就是 u u u 中符号函数 s i g n ( x ) sign(x) sign(x)的存在,即使经过积分一次后得到的 x 2 x_2 x2 依然避免不了震荡。因为数值积分嘛,你懂的。
所以为了能够实现离散系统的最速控制,消除跟踪-微分器的稳态颤振,韩教授又搞了一个离散最速控制函数,这个比较复杂一点。这里我们只负责介绍跟踪-微分器的思想,关于离散最速控制函数放到下一部分(ADRC的公式以及参数整定)再讲。
总之,这里的跟踪-微分器是为了解决1、2两个问题:安排过渡过程以及提供微分信号。
注意:其实第二个问题在ADRC里被拆成两部分了,由误差提取误差微分包括了两部分:指令的微分和输出量的微分(因为误差等于指令减去输出量)。指令的微分是由跟踪-微分器搞定的,而输出量的微分是由后面的扩张状态观测器搞定的。
3. 加权和的策略不一定最好——非线性反馈
传统的线性反馈方式(就是误差直接乘上一个增益)在收敛速度以及抗扰动能力上存在不足。
ADRC的方案是 用非线性函数代替传统的增益(用非线性反馈代替线性反馈)。
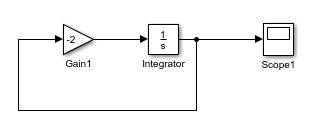
这里也可以举个例子,比较两个系统,分别使用线性反馈和非线性反馈:(1) x ˙ = − K x \dot{x}=-Kx x˙=−Kx
以及 (2) x ˙ = − K ∗ s i g n ( x ) ∗ ∣ x ∣ α ( α < 1 ) \dot{x}=-K*sign(x)*|x|^\alpha(\alpha<1) x˙=−K∗sign(x)∗∣x∣α(α<1)
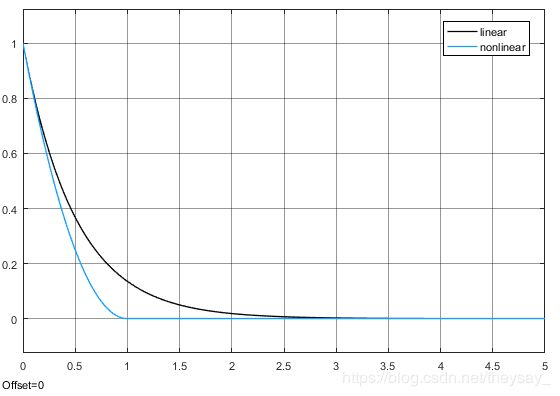
假设 x 0 ≠ 0 x_0≠0 x0=0,则可以证明系统(2)能在有限时间内收敛到0,而系统(1)是指数收敛的,意思是永远收敛不到0。
可以看到非线性反馈更快地收敛到0了,不过需要注意的是非线性反馈相对于线性反馈的快速性的优势只在 x < 1 x<1 x<1的时候才有,而且在靠近 x = 0 x=0 x=0的附近容易引起颤振。
4. 积分反馈的副作用——扩张状态观测器
积分的主要作用之一就是消除扰动(可以认为它是简单的扰动观测器),但是积分起作用比较慢,而且还会引起超调。
所以ADRC直接把积分舍弃了,使用扩张状态观测器来观测总扰动,将系统补偿成纯积分链(不知道这个学名是啥)的形式。这样控起来就容易多了,可以说,扩张状态观测器是ADRC的灵魂和精髓所在,在它面前,前面几个都是次要的。
用一个例子说明一下上面所说的几点:
假设某系统 x ˙ = u + w \dot{x}=u+w x˙=u+w,其中 x x x为状态量(也是被控量), u u u为控制量, w w w为未知的总扰动(包括模型偏差或者外部扰动等等)。
比较两种情况,一种是 w w w没有被补偿,在线性反馈的基础上加上积分反馈去抵消,以达到无静差的目的。另一种是把 w w w补偿掉,只剩一个积分环节,采用普通的线性反馈。
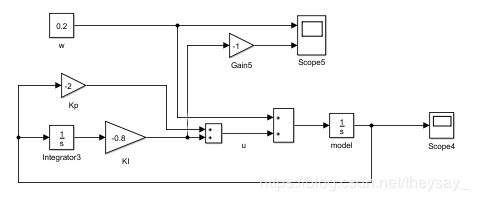
第一种情况: u = − K P ∗ x − K I ∗ ∫ x d τ u=-K_P*x-K_I*\int{x}d\tau u=−KP∗x−KI∗∫xdτ
w = 0.2 , x 0 = 1 w=0.2,x_0=1 w=0.2,x0=1,取 K P = 2 K_P=2 KP=2
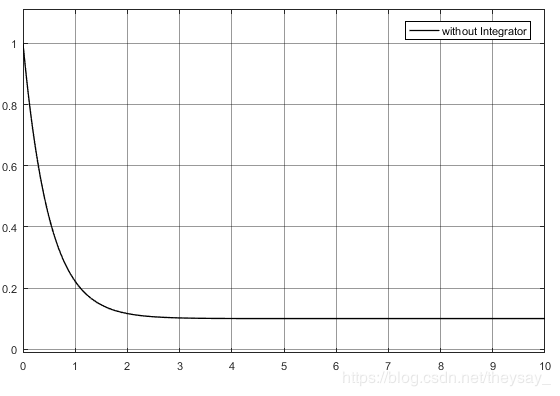
先看一下没有积分反馈(也就是 K I = 0 K_I=0 KI=0)时 x x x最后能控成什么样子
得到的 x x x 的仿真结果为:
接着给出有积分反馈(如上上图,也就是 K I = 0.8 K_I=0.8 KI=0.8)时 x x x最后能控成什么样子
得到的 x x x 的仿真结果为:
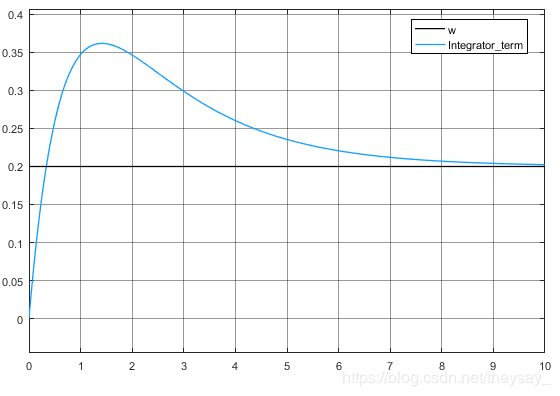
再看一下 K I ∗ ∫ x d τ K_I*\int{x}d\tau KI∗∫xdτ与 w w w的对比情况
这里说的是积分器对扰动的观测效果,其实应该是补偿效果。可以看到积分环节产生的超调现象比较明显,并且如果积分增益取大了则超调就大,如果取的小则收敛就慢,没辙。
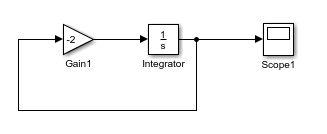
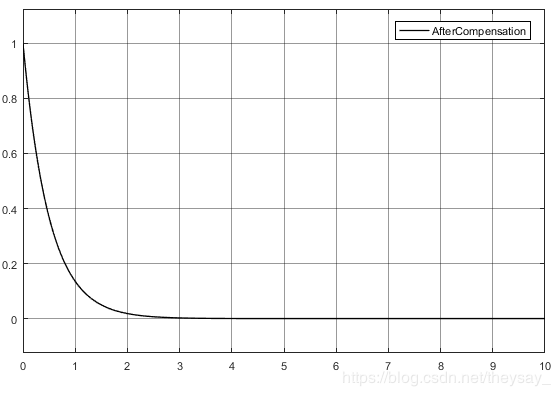
第二种情况我们把扰动去掉(假设被观测出来然后补偿掉了),只用一个 K P K_P KP来控,那么结果的就很容易想到了:闭环之后这是一个单纯的惯性环节,没有超调,收敛的快慢只和增益有关,增益越大,收敛越快。
对于一阶系统来说,就是把模型补偿成一个积分环节( n n n阶系统补偿之后就是 n n n个积分串在一起)。
通过对比可以发现,还是把扰动补偿掉更好。
利用扩张状态观测器,ADRC理论上可以把一个任意阶的系统补偿成任意阶的积分链,然后就可以用简单的线性控制方法去实现控制了,而且也能得到较好的控制效果。所以说扩张状态观测器是ADRC的精髓,把前面的跟踪微分器换成一个别的什么的线性滤波器没问题,把非线性反馈换回线性反馈没问题,但是这个观测扰动并补偿的思想不能丢。
ADRC的公式以及参数整定
前面一直是一些简单的例子解释说明ADRC的各个组成部分,只是对概念的理解。接下来要给出ADRC的公式以及我对其参数的理解,理解参数的含义能够大大提升参数整定的能力。
下次再写。
一、跟踪微分器(TD)
二、非线性反馈函数
三、扩张状态观测器(ESO)
ADRC应用到二阶导弹模型
这部分的饼也先画上,其实模型和脚本我都已经弄好了。
matlab脚本
simulink模型
结语
发现这个ADRC还真挺好用的,而且里面的一些思想其实和一些非线性控制都是相通的。
比如指令滤波和指令微分器,这个在反步法里也是标配的,不过反步法里的指令微分直接拿来做前馈补偿的,不是用来计算误差微分的。
再比如非线性反馈,这是(终端)滑模控制里的嘛,不过滑模控制证明稳定性更容易一些。
最后是这个扩张状态观测器,本来是在龙伯格观测器基础上扩张了一个误差状态,然后把里面的线性项换成了非线性项,使其收敛更加快速,但是改造完之后这个ESO就跟高阶滑模观测器很像了。