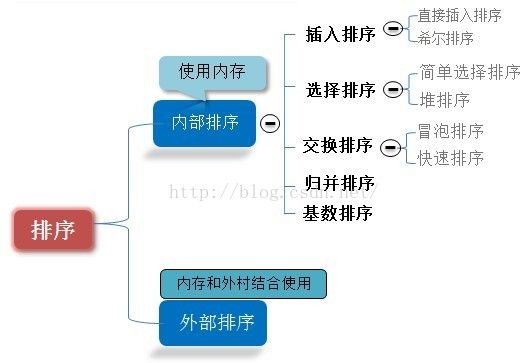
数据结构之排序算法(五)-直接插入排序,希尔排序,直接选择排序
直接插入排序:时间复杂度:O(n^2)
基本算法思路是:把后面待排序的记录按其关键字的大小逐个插入到一个已经排好序的有序序列中,直到所有记录插完为止,得到一个新的有序序列。(无序插入前面有序)
算法步骤:对数组a
1,设置监视哨a[i],将待插结果的值赋值给temp
2, 设置开始查找的位置j=i-1;
3,在数组j后面搜索,如果temp
4,将temp插入到a[j+1]的位置
文字不行,直接上代码:
public class InsertSort {
public static void main(String[] args) {
int[] a={49,38,65,52,13,25,45,62,20};
insertSort(a);
System.out.print("排序结果:");
for(int i=0;i=0&&temp
第1趟: 38 49 65 52 13 25 45 62 20
第2趟: 38 49 65 52 13 25 45 62 20
第3趟: 38 49 52 65 13 25 45 62 20
第4趟: 13 38 49 52 65 25 45 62 20
第5趟: 13 25 38 49 52 65 45 62 20
第6趟: 13 25 38 45 49 52 65 62 20
第7趟: 13 25 38 45 49 52 62 65 20
第8趟: 13 20 25 38 45 49 52 62 65
排序结果:13 20 25 38 45 49 52 62 65 希尔排序又叫缩小增量排序。基本算法思路是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序。(说白了还是直接插入排序,只不过每次增量不一样)
算法步骤:
我们简单处理增量序列:增量序列d = {n/2 ,n/4, n/8 .....1} n为要排序数的个数
即:先将要排序的一组记录按某个增量d(n/2,n为要排序数的个数)分成若干组子序列,每组中记录的下标相差d.对每组中全部元素进行直接插入排序,然后再用一个较小的增量(d/2)对它进行分组,在每组中再进行直接插入排序。继续不断缩小增量直至为1,最后使用直接插入排序完成排序。
代码:
public class ShellSort {
public static void main(String[] args) {
int[] a={49,38,65,52,13,25,45,62,20};
shellSort(a);
System.out.print("排序结果:");
for(int i=0;i=1){ //以各种不同的间隔距离d进行排序
//下面是直接插入排序
for(int i=d;i=0&&temp
排序结果:13 20 25 38 45 49 52 62 65 简单选择排序:时间复杂度O(n^2)
算法基本思路:指每次从待排序的记录中选出关键字最小(最大)的记录,顺序放入已排好序的有序序列中,直到全部排完
在要排序的一组数中,选出最小(或者最大)的一个数与第1个位置的数交换;然后在剩下的数当中再找最小(或者最大)的与第2个位置的数交换,依次类推,直到第n-1个元素(倒数第二个数)和第n个元素(最后一个数)比较为止。
算法步骤:
第一趟,从n 个记录中找出关键码最小的记录与第一个记录交换;
第二趟,从第二个记录开始的n-1 个记录中再选出关键码最小的记录与第二个记录交换;
以此类推.....
第i 趟,则从第i 个记录开始的n-i+1 个记录中选出关键码最小的记录与第i 个记录交换,
直到整个序列按关键码有序。
代码:
public class SelectSort {
public static void main(String[] args) {
int[] a={49,38,65,52,13,25,45,62,20};
seletSort(a);
System.out.print("排序结果:");
for(int i=0;i输出结果:
排序结果:13 20 25 38 45 49 52 62 65 总结:
算法复杂度的记法:
“三个简单排序”
冒泡 O(n^2)
插入 O(n^2)
选择 O(n^2)
“三个复杂排序”
快排 O(nlogn)
归并 O(nlogn)
堆排 O(nlogn)
希尔排序:O(n^1.3)