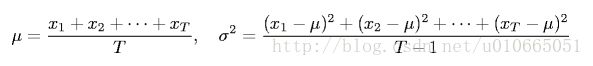算法分析学习笔记（一） - 动态连通性问题的并查集算法（下）

三. 实际应用——解决物理化学中的渗滤模型问题

     该问题来自于http://coursera.cs.princeton.edu/algs4/assignments/percolation.html，问题的原版描述如下：

      Percolation. Given a composite systems comprised of randomly distributed insulating and metallic materials: what fraction of the materials need to be metallic so that the composite system is an electrical conductor? Given a porous landscape with water on the surface (or oil below), under what conditions will the water be able to drain through to the bottom (or the oil to gush through to the surface)? Scientists have defined an abstract process known as  percolation to model such situations.

     简单解释下，这就是科学家常说的“渗滤模型”，它通常用来建模如下情况：1）给定一个由绝缘体和导体构成的复合材料，问导体所占比例为多少时该复合材料能够导电？2）给定一块表面上有水或油的多孔地形，在什么情况下水或者油能渗漏到底层去？

     我们用一个N*N的网格来建模这一系统，其中每一个网格要么是开放的（open），要么是阻塞的（blocked），我们在开放网格的基础上定义“满”（full）网格——它是一种特殊的开放网格，可通过上，下，左，右四个方向的一系列临近网格连接到顶层第一行的开放网格上去。若底层行存在满网格，我们就说该系统是“可渗滤的”，也就是说顶层和底层之间存在开放路径，电或者是水可以从顶层渗漏到底层去。图3-1左边是可渗滤系统，而右边则不是。

图3-1 渗滤模型

图3-2 添加虚拟节点的技巧

3.1 要解决的问题     

     假设每一个网格都是独立的，它成为开放网格的概率是p，科学家关心的问题是：整个系统是可渗滤的概率有多大？若p为0，每个网格都是阻塞的，那么整个系统就是不可渗滤的；若p为1，那么整个系统就是可渗滤的。当N足够大，一定存在一个阀值p*，当p大于p*时系统可渗滤，当p小于p*时系统不可渗滤，我们的任务就是找出p*的值。

     我们用有序对（i，j）对网格进行编号，按题目要求，(i，j)的取值在1和N之间，其中（1，1）是最左上角的网格。但具体的实现上我们不打算用二维数组，而是采取将二维数组映射为一维数组的方式，这么做的理由是因为我们要使用并查集算法，而并查集算法是基于一维数组实现的。API的Java语言描述如下所示：

public class Percolation {
   public Percolation(int N)              // create N-by-N grid, with all sites blocked
   public void open(int i, int j)         // open site (row i, column j) if it is not already
   public boolean isOpen(int i, int j)    // is site (row i, column j) open?
   public boolean isFull(int i, int j)    // is site (row i, column j) full?
   public boolean percolates()            // does the system percolate?

}

3.2 具体实现参考     

     实现上，我们用一个一维数组op[]来存储映射过的网格（i，j），op的大小为N * N + 2。我们在原来的N个顶层节点和底层节点的基础上再添加两个虚拟节点，其中op[0]为虚拟顶层节点，op[N * N + 1]为虚拟底层节点，并将各顶层节点与虚拟顶层节点建立连接，各底层节点与虚拟底层节点建立连接，这样只需一次调用就可以检查该模型是否是可渗滤的，如图3-2所示。

private final int size;

private boolean[] op; // mark whether it is open or blocked

private final int vtop;

private final int vbot;

private WeightedQuickUnionUF wquf;

private WeightedQuickUnionUF backwash;
public Percolation(int N) {
        if (N < 1) {
                throw new IllegalArgumentException("N must be >= 1");
        }
        size = N;
        wquf = new WeightedQuickUnionUF(size * size + 2);
        backwash = new WeightedQuickUnionUF(size * size + 1);
        // op[vtop] is virtual top and op[vbot] is virtual bottom
        op = new boolean[size * size + 2];
        vtop = 0;
        vbot = size * size + 1;

}  

     open函数的实现要考虑左，右，上，下四个方向的邻居，若邻居处于打开状态，则需要通过并查集算法建立连接；若被打开的网格在顶层或底层，则也需要分别与虚拟顶节点和虚拟底节点建立连接，而isOpen，isFull和perlocates函数的实现就要相对简单一些，backwash只有虚拟顶节点没有虚拟底节点，用来防止在底部出现孤立的伪“满网格”。完整的实现请参见https://github.com/leesper/algorithms_4ed/blob/master/ch1/Percolation.java

        /**        

        * Open the (i, j) site in N-by-N grid.        

        */
        public void open(int i, int j) {
                if (isOpen(i, j)) 
                        return;

                op[xyTo1D(i, j)] = true;

                if (isTopRow(i)) {
                        op[vtop] = true;
                        // make sites in top row union to virtual top
                        wquf.union(vtop, xyTo1D(i, j));
                        backwash.union(vtop, xyTo1D(i, j));
                }

                if (isBotRow(i)) {
                        op[vbot] = true;
                        // make sites in bottom row union to virtual bottom
                        wquf.union(vbot, xyTo1D(i, j));
                }

                // up
                if (checkValid(i - 1, j) && isOpen(i - 1, j) 
                                && !wquf.connected(xyTo1D(i - 1, j), xyTo1D(i, j))) {
                        wquf.union(xyTo1D(i - 1, j), xyTo1D(i, j));
                        backwash.union(xyTo1D(i - 1, j), xyTo1D(i, j));
                }
                // down
                if (checkValid(i + 1, j) && isOpen(i + 1, j) 
                                && !wquf.connected(xyTo1D(i + 1, j), xyTo1D(i, j))) {
                        wquf.union(xyTo1D(i + 1, j), xyTo1D(i, j));
                        backwash.union(xyTo1D(i + 1, j), xyTo1D(i, j));
                }
                // left
                if (checkValid(i, j - 1) && isOpen(i, j - 1)
                                && !wquf.connected(xyTo1D(i, j - 1), xyTo1D(i, j))) {
                        wquf.union(xyTo1D(i, j - 1), xyTo1D(i, j));
                        backwash.union(xyTo1D(i, j - 1), xyTo1D(i, j));
                }
                // right
                if (checkValid(i, j + 1) && isOpen(i, j + 1)
                                && !wquf.connected(xyTo1D(i, j + 1), xyTo1D(i, j))) {
                        wquf.union(xyTo1D(i, j + 1), xyTo1D(i, j));
                        backwash.union(xyTo1D(i, j + 1), xyTo1D(i, j));
                }
        }

        /**        

        *   return true if the (i, j) site in N-by-N grid is open.        

        */
        public boolean isOpen(int i, int j) { 
                if (!checkValid(i, j)) {
                        throw new IndexOutOfBoundsException("index i out of range");
                }
                return op[xyTo1D(i, j)] == true;
        }

        /**        

        *   return true if the (i, j) site in N-by-N grid is full.        

        *   A full site is an open site that can be connected to an         

        *   open site in the top row via a chain of neighboring         

        *   (left, right, up, down) open sites.                 

        */
        public boolean isFull(int i, int j) { 
                if (!isOpen(i, j)) {
                        return false;
                }
                return backwash.connected(vtop, xyTo1D(i, j));
        }

        /**        

        *   return true if this N-by-N system is percolated        

        */
        public boolean percolates() { 
                return wquf.connected(vtop, vbot);
        }

3.3 估算阀值的方法     

     我们用Monte Carlo模拟来估算渗滤阀值：1）将所有网格初始化为阻塞态；2）随机选择一个阻塞的网格（i,j），打开它，不停地重复步骤2）直到系统渗滤为止；3）打开的网格数占所有网格数的比值即为渗滤阀值的一次估计。不断地重复此步骤T次得到的采样平均即为渗滤阀值的估计值，其标准差则描述了阀值图像的陡峭程度，如图3-3和3-4所示。

3-3 阀值图像

3-4 采样平均与方差

     我们用一个PerlocationStat类来完成这一模拟方法，如下所示。完整实现请参考 PercolationStats.java。

public class PercolationStats {
   public PercolationStats(int N, int T)    // perform T independent computational experiments on an N-by-N grid
   public double mean()                     // sample mean of percolation threshold
   public double stddev()                   // sample standard deviation of percolation threshold
   public double confidenceLo()             // returns lower bound of the 95% confidence interval
   public double confidenceHi()             // returns upper bound of the 95% confidence interval
   public static void main(String[] args)   // test client, described below

}

3.4 有什么招式值得一学？

（1）Monte Carlo模拟方法的应用——多次重复，取平均值和方差来估算阀值；

（2）用虚拟节点的技巧来避免遍历全部的顶层和底层节点（平方复杂度）；

四. 再谈“举一反三”

     从踏入学校的第一天起，老师和父母就在不断地告诫我们，学习一定要举一反三，不要钻牛角尖。那么到底什么才是举一反三呢？举一反三强调的其实是一种“知识迁移”的能力，通常说来，我们在生活，工作和学习中遇到的问题无非是两类问题——曾经遇到过的问题和从来没遇到过的问题。对于曾经遇到过的问题，知道方法也就知道怎么解决了，除非你是个不断在同一个坑里摔倒的缺心眼。面对从来没遇到过的新问题，要不断摸索，不断试错，不断栽跟头，才有成功解决的那天。但是如果你懂得知识迁移，你还是能发现某些规律的。你可能通过观察发现所谓的新问题其实是某个已解决问题的另一种表现形式，那么你可以用旧的方法解决新的问题；或者你发现新问题与某个已解决的问题类似，把那个问题的思路或者结论稍作应用，也能解决新问题；又或者你解决的问题多了，经验丰富了，你自己创造性地用新的方法解决了新的问题，得到了提高，这些都是“举一反三”的具体体现。匈牙利数学家乔治波利亚在他的经典名著《怎样解题：数学思维的新方法》中提到，如果你在解决一个问题时，发现它似曾相识——你解决过一个类似的问题，那么你就要回忆，我解决那个问题的方法是什么？得到什么样的结论？可以利用它的方法来解决这个问题吗？可以利用它的结论来解决这个问题吗？既利用方法又利用结论能解决这个问题吗？接下来我们就利用剩下一半的篇幅，通过一个经典的搜索算法来谈谈我对举一反三的一些感受。

4.1 binary search：经典的二叉搜索算法

     二叉搜索算法是一个妇孺皆知的经典算法，它是一种折半查找的搜索策略，使用它有一个前提，即数组必须是已经排好序的，这样我们每次都通过它的中点去确定我们要找的那个元素到底在中点的左边还是右边，然后减半……因为每次都减半，所以算法效率很高，对数时间内就能确定要找的元素到底在不在数组中，代码如下所示（以整型数组为例）。

func binarySearch(key int, arr []int) int {
        low := 0
        high := len(arr) - 1
        for low <= high {
                mid := (low + high) / 2
                if key < arr[mid] {
                        high = mid - 1
                } else if key > arr[mid] {
                        low = mid + 1
                } else {
                        return mid
                }
        }
        return -1
}

     

对于二叉搜索算法来说，它解决的是在一个有序数组中快速查找元素的问题，它采用的策略是减半策略，结论是该算法能够在logN的时间内找到或找不到元素，记住这些基本点，它们都有可能是解决新问题时的“迁移点”，下面我们就来通过几个例子分析一下。

4.2 知识的迁移：解决M-求和问题

     M-求和问题的定义是：给定N个不同的整数，问有多少个M元组加起来的和为0？这个问题在计算几何学中较为常见。这里我们先来尝试解决一些简单的情况，比如我们先来看看2-求和问题：给定N个不同的整数，问有多少个2元组（x，y），使得x和y的和为0？最笨的办法当然是暴力方法了——遍历两遍数组，然后一个一个地检查不同的组合，把所有的可能情况全部找出来，代码如下所示。

// N^2

func twoSum(arr []int) int {
        count := 0
        for i := 0; i < len(arr); i++ {
                for j := i + 1; j < len(arr); j++ {
                        if arr[i] + arr[j] == 0 {
                                count++
                        }
                }
        }
        return count;
}

这样的算法简单粗暴，但低效，如果数组足够大，这个算法所花的时间是我们无法忍受的，但至少我们可以以它作为出发点优化算法效率。回过头来想一想，该问题想问的其实是能不能“找到”两个数，它们的和为0，既然提到了“找”，那它就是一个查找问题，那何必要用两层循环去穷举呢？完全可以用二叉搜索算法去查找-arr[i]，这样算法的效率就提高到了，可以解决实际问题了，代码如下所示：

// NlogN

func twoSumFast(arr []int) int {
        sort.Ints(arr)
        count := 0
        for i := 0; i < len(arr); i++ {
                if binarySearch(-arr[i], arr) > i {
                        count++
                }
        }
        return count
}

     故事讲到这里并没有结束，书上的一道课后习题让设计一个更快的线性时间的算法来解决这个问题，回过头来想想，既然整数和能够为0，说明数组中的整数有正有负，这一点还没利用。那么数组排序后，负数都在左边而正数都在右边，我们就可以用两个游标从数组的两头往中间走：若两数相加为0，则表示找到一个数对；若相加为负数，说明左边那个负数太小，要往右移动一位；若相加为正数，说明右边那个正数太大，要往左移动一位，这个过程一直持续到游标碰头为止，代码如下所示。

// N

func twoSumFaster(arr []int) int {
        sort.Ints(arr)
        l := 0
        r := len(arr) - 1
        count := 0
        for l < r {
                if arr[l] + arr[r] == 0 {
                        count++
                        l++
                        r--
                } else if arr[l] + arr[r] > 0 {
                        r--
                } else {
                        l++
                }
        }
        return count
}

     有了解决2-求和问题的经验，面对3-求和问题，我们就心里有数了。3-求和问题是，给定N个不同的整数，问有多少个3元组的和为0？不用写代码，光类比我们就可以知道，最笨的办法解决3-求和问题算法效率一定是 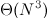，那么我们利用解决2-求和问题的方法和结论来解决3-求和问题，一定能够将效率提高到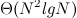和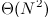 ，代码如下所示。

// N^3

func threeSum(arr []int) int {
        count := 0
        for i := 0; i < len(arr); i++ {
                for j := i + 1; j < len(arr); j++ {
                        for k := j + 1; k < len(arr); k++ {
                                if arr[i] + arr[j] + arr[k] == 0 {
                                        count++
                                }
                        }
                }
        }
        return count
}

// N^2logN

func threeSumFast(arr []int) int {
        count := 0
        for i := 0; i < len(arr); i++ {
                for j := i + 1; j < len(arr); j++ {
                        if binarySearch( -(arr[i] + arr[j]), arr ) > j {
                                count++
                        }
                }
        }
        return count;
}

// N^2

func threeSumFaster(arr []int) int {
        count := 0
        for i := 0; i < len(arr); i++ {
                key := arr[i]
                l := i + 1
                r := len(arr) - 1
                for l < r {
                        if key + arr[l] + arr[r] == 0 {
                                count++
                                l++
                                r--
                        } else if key + arr[l] + arr[r] > 0 {
                                r--
                        } else {
                                l++
                        }
                }
        }
        return count
}

4.3 知识的再迁移——求数组局部最小值

     同样给定N个不同整数的数组arr，这次我们要找到一个局部最小值，即i，使得arr[i] < arr[i-1]且arr[i] < arr[i+1]。又是一个查找的问题，我们同样可以进行一下知识迁移：既然我们已经见过二叉搜索算法，那么我们可以不可以利用它来解决这个问题呢？首先我们肯定不能对这个数组进行事先排序，那样就把局部最小值破坏了，回想到二叉搜索算法是通过检查中点来进行搜索的，那么我们可以试一试借鉴这一策略来查找局部最小值，先找到中点mid，如果arr[mid] < arr[mid+1]且arr[mid] < arr[mid-1]，那么我们找到了，否则哪边邻居小我们就折半到哪一边去找。具体的实现代码如下所示，这里用了一点递归的技巧。

func localMin(arr []int) int {
        low := 0
        high := len(arr) - 1
        return localMinRecur(arr, low, high)
}

// 2lgNfunc localMinRecur(arr []int, low, high int) int {
        mid := (low + high) / 2
        if mid == len(arr) - 1 || mid == 0 {
                return -1
        }
        if arr[mid] < arr[mid - 1] && arr[mid] < arr[mid + 1] {
                return mid
        }
        // search in the half with the smaller neighbor
        var mLeft, mRight int
        if arr[mid - 1] < arr[mid] {
                mLeft = localMinRecur(arr, low, mid - 1)
        }

        if arr[mid + 1] < arr[mid] {
                mRight = localMinRecur(arr, mid + 1, high)
        }

        if mLeft != -1 {
                return mLeft
        }
        return mRight
}

4.4 结论

     从上面的例子中我们就能看到知识迁移能力在算法学习中的重要性，当然这里的例子都是比较简单的例子，在实际解决问题的过程中，有时候不是那么容易就能实现迁移的，只有在不断的解决问题的过程中，多看，多想，多总结，在积累丰富经验的基础上，通过细致的观察并运用创造性思维，才能在看似没有联系的知识之间建立联系，实现迁移，这其中不断复习和总结的过程很重要。v_July_v哥说，学习一个算法，先知其解决什么问题，后知其运用什么样的策略。知道了应用场景，才能把学会的算法用来解决实际问题；知道了解决的策略，才能在面对新问题设计新算法时有所借鉴。比如你想把算法效率提高到对数级，你就得先发散思维——都哪些算法是对数级的，它们的策略是什么？结论又是什么？怎样用在我当下解决的新问题上？也许灵感就在其中。在本系列算法分析的学习笔记中，都会采用这样的介绍形式。即围绕一个相对独立的专题展开讨论，先明确我们要解决的是什么样的问题，然后分析各种经典算法的方法，它们的结论（主要是算法效率的数学分析），最后列举一些利用这些方法和结论解决问题的实际例子，并归纳总结一些值得学习的招数。