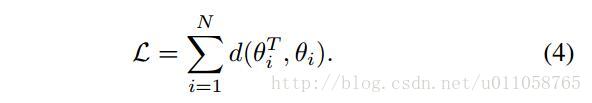Cascaded Pose Regression

摘要

我们提出一种快速和准确的称为级联姿态回归（CPR）算法来计算图像中的对象的2D姿态。 CPR算法逐步细化随意指定的初始姿态，其中每一次姿态修正由不同的回归器确定。 每一个回归器执行简单图像测量依赖于先前回归器的输出结果; 整个系统从人工注释的训练数据集中自动学习。 CPR不限于刚性变换：“姿态”是对象外观的任何参数化变化，例如可变形和关节对象的自由度。 我们比较CPR与标准回归技术和人工标定（从冗余的人类注释计算）。 在三个不同的数据集（小鼠，脸，鱼）上的实验表明CPR是快速的（每个姿势估计2-3ms），准确（接近手工标定），并且容易从少量的标记数据训练。

介绍

检测和定位是视觉的最有用的功能之一。检测包括给出问题“是图像中的对象/类别x”的一位答案：本地化是一个更微妙的问题：在其最简单和最流行的形式[11]中，它包括识别最小矩形区域包含相关对象的图像。这对于图像中的主要几何自由度是平移和缩放的类别（例如前脸和行人）是完全足够的。更一般地，人们希望恢复姿态，即影响对象的图像的多个参数。最常见的姿态是指刚性物体的几何变换[23]，包括铰接物体的配置，例如人体四肢或车辆布局[21]。更广泛地说，姿态是物体外观的任何系统的和可参数化的变化[5]。计算对象的姿态有两个不同的原因：（1）由于对象可变性，执行检测的唯一方式是显式地计算和分解姿态，（2）姿态是视觉模块的期望输出。 在这项工作中，我们对后者感兴趣：我们希望估计物体的粗略初始位置的姿势，例如跟踪器提供的姿势。

在位置和尺度上对象定位的主要方法是使用“滑动窗口”，即重复二进制分类任务，“是位置y处的对象x”，用于姿态参数的细粒度采样。 虽然这产生了大量的测试，滑动窗口方法可以通过级联[28]，距离变换[13]，分支界限搜索[20]和粗略到精细的方法[15]变得更高效。 这样的方法可以通过重复回答形式为“在具有姿势θ的位置y处的对象x”的查询而扩展到更复杂的姿态概念，对于姿态θ的每个分区有一个查询。 例如，对于面部检测，通常为不同水平的平面外旋转训练单独的分类器[28]。 当然，这导致任务的组合爆炸，虽然有效的搜索策略可以帮助[16]，最终这种方法可能无法扩展到更复杂的概念的姿势。

在这项工作中，给定对对象位置的粗略估计，我们直接回答问题“什么是对象x的姿势θ？”，恢复姿势而不执行潜在的昂贵和分支搜索。原则上，标准回归技术完全如此[17,10]。虽然对于计算机视觉中的某些回归任务已经成功[30,1]，但其对更一般姿态估计的适用性仍不清楚。正如在增强回归[17,10,30]，我们建议学习一个固定的线性序列（级联）弱回归（在我们的情况下随机蕨类植物）。与先前迭代回归方法的主要区别是使用姿态索引特征[16]：其输出特征取决于图像数据和姿态的当前估计。通过假定姿态索引特征的某些弱不变性质，我们推导了用于姿态估计的原理性算法，我们称为级联姿态回归（CPR）。我们证明CPR收敛在指数速率下弱弱的学习能力弱于强化回归通常所需的概念。可以用令人惊讶的少量数据（O（100）标记的训练示例）学习准确的模型。 CPR快（每个姿态估计2-3ms），准确（接近人的性能），并且容易地在不同的对象类别上训练。

我们的主要贡献是：（1）提出快速级联姿态回归算法，其对各种各样的对象类别产生精确的姿态估计。（2）使用冗余注释数据，我们评估人工标定数据的性能，并定义一个感知距离函数来比较姿势注释。 （3）对算法的综合实验评价和对许多数据集的有希望的结果。 我们从下面的相关工作开始。

使用随场景或对象信息而变化的特征在计算机视觉中具有悠久的历史。Dickmanns和Graefe [9]提出了一种实时控制方案，其在可能包含用于动态视觉系统的有用信息的位置处稀疏地计算特征。 Goncalves et al迭代的计算3D臂姿态，用每个改进的姿态估计精化2D图像特征; 最近，Ramanan [26]在多阶段姿态估计程序中使用了类似的想法。 Fleuret和Geman [16]创造了术语“姿势索引特征”来指代相对于给定姿势定义的特征; 在这项工作中，我们采用相同的术语。 然而，与[16]不同，我们使用姿态索引特征进行回归而不是分类，从而允许我们直接执行姿态估计。

早期的姿态估计工作包括蛇[19]，模板匹配[29]和主动外观模型[8]。虽然已经提出了在思想上类似于使用学习来驱动优化的CPR的扩展[27]，但是通常这些方法需要手动定义的能量函数来测量拟合优度。另一种相关方法是结构化输出预测[4]，其为学习回答“在具有姿态θ的位置y处的对象x”提供了原则性的表达式。然而，与标准分类一样，仍然需要高效的搜索/推理技术[20,4]。许多现代检测方法包括将对象分解为各个组件，分别检测每个组件，然后通过灵活部分模型组合它们[7,12,5]。这种方法尽管在检测关节对象方面是有效的，但还没有显示返回精确的姿态估计。在最近的工作中，Ali et al。 [2]使用姿态索引特征执行关节对象的检测，将这些特征直接集成到升压级联中，以及Ozuysal¨等人。 [25]使用在检测之前的姿态估计，在姿态估计上调节它们的分类器。这两种方法提出了新的和有趣的方向将姿态集成到检测;然而，在这项工作中，我们专注于姿态估计问题本身。

2. Cascaded Pose Regression

为了清楚地讨论对象姿态和外观，我们假设存在一些未知的图像形成模型G：O×Θ→I，其取对象出现o∈O和姿态θ∈Θ，并且生成图像I∈I。我们从不 有明确的访问G或o; 然而，它们对于随后的推导是必要的。 例如，我们可以写出Iθ1= G（o，θ1）和Iθ2= G（o，θ2）来表示两个配置θ1和θ2中的同一物体o的两个图像。 我们假设G（o1，θ1）= G（o2，θ2）iff o1 = o2和θ1=θ2，否则唯一地估计姿态可能是不可能的。

我们要求Θ和操作◦形成一个组。 给定两个姿态θ1，θ2，我们写θ=θ1◦θ2表示通过组合θ1和θ2形成的新姿势，θ表示θ的倒数，e表示单位元素。 为了测量两个姿态之间的相对误差，我们需要一个函数d：Θ×Θ→R其中d（θ1，θ2）只能取决于相对姿态θ1◦θ2，或者等效地d（θδ◦θ1，θδ◦θ2） = d（θ1，θ2），对于所有θ1，θ2，θδ∈ Θ。

2.1. Pose-Indexed Features and Weak Invariance

如上所述，在这项工作中，我们依赖pose-indexed特征。 pose-indexd特征仅仅是形式h：Θ×I→R的函数。我们说h是弱不变量，如果Θθ，θδ∈以下成立：

h(θ, G(o, e)) = h(θδ ◦ θ, G(o, θδ)), (1)

或者等价地，如果Θθ1，θ2，θδ∈ Θ：

h(θ1, G(o, θ2)) = h(θδ ◦ θ1, G(o, θδ ◦ θ2)). (2)

当且仅当（1）成立时，很容易证明（2）成立。 说明上述的另一种方式是h（θ1，G（o，θ2））仅取决于物体o和输入姿态θ1和真姿态θ2之间的相对姿态θ1◦θ2。 换句话说，如果在给定姿态的一致（不一定正确）估计的情况下，h的输出是恒定的，则h是弱不变的。 使用标准操作编写弱不变特征导致本身弱不变的特征。

注意，如上定义的不变性是比一般姿态不变性弱得多的要求，其可以表示如下：h（G（o，θ））= h（G（o，θδ◦θ））。 设计满足后面的定义的不变函数是非常困难的，而我们的定义需要不变性，只有当给定姿态的一致估计。 还值得比较（2）与在[16]中引入的“平稳性假设”。 使用这里定义的符号，平稳性假设的非概率形式可以写为h（θ1，G（o，θ1））= h（θ2，G（o，θ2））。 换句话说，其状态h（θ，G（o，θ））是恒定的，而与θ的值无关。 观察到（2）是平稳性假设的一个非常自然的，虽然更强的泛化。

我们的弱不变假设证明了随后的推导，并允许我们证明所得算法的强收敛速度。 在理想条件下，我们可以证明（2） 然而，如在[16]中，我们观察到，在实践中（2）将经常被违反。 然而，如我们将证明，使用弱不变性假设导出的算法在实践中非常有效。

Pose-Indexed Control Point Features

在所有的实验中，我们使用极其简单和快速的计算控制点特征[22,24]。 在我们的实现中，每个控制点特征被计算为在预定义图像位置处的两个图像像素的差。 更具体地，每个特征hp1，p2由两个图像位置p1和p2定义，并且通过计算hp1，p2（I）= I（p1）-I（p2）来评估，其中I（p）表示 在位置p图像的灰度值。

除了它们在实际应用中的速度和令人惊讶的有效性[24]，上述特征的优点是它们直接通过姿态索引。 例如，假设物体姿势由平移，旋转，缩放和宽高比（或这些参数的某些子集）指定。 对于每个姿态θ，我们可以定义相关联的3×3单应性矩阵Hθ，在齐次坐标中表达p，并且定义h p1，p2（θ，I）= I（Hθp1）-I（Hθp2）。 我们可以容易地将这种方法扩展到铰接对象，其中每个部分具有旋转，缩放和宽高比，通过将单独的单应性矩阵与每个部分相关联。 参见图2。

在附录中（在项目网站上），我们表明以上述方式定义的h（θ，I）在某些假设下是弱不变的。 然而，一般来说，设计弱不变姿态索引特征可能是非常具有挑战性的，并且当将我们提出的框架应用于新颖问题时需要仔细考虑。

2.2. Cascaded Pose Regression

我们现在描述级联姿态回归R =（R1，…，RT）的评估和训练程序，分别如图3和图4所示。 我们将训练级联回归R =（R1，…，RT），使得在给定输入姿态θ0的情况下，通过计算来评估R（θ0，I）

θt = θt−1 ◦ Rt(ht(θt−1, I)), (3)

从t = 1。 。 。 T并最终输出θT（参见图3）。 训练每个分量回归器Rt以尝试使用（姿态索引）特征ht最小化真实姿态与由先前分量计算的姿态之间的差异。 我们的目标是优化以下损失：

我们开始计算θ0=argminθPi d（θ，θi），并为每个i设置θ0i =θ0。 θ0是单个姿态估计，其给出最低的训练误差而不依赖于任何分量回归。 我们现在描述给定R1的训练Rt的过程。 。 。 ，Rt-1。 在每个阶段t中，我们通过随机生成姿态索引特征ht并且针对具有先前姿态估计θi t-1的每个训练样本ii计算xi = ht（θi t-1，I i）来开始训练。 我们的目标是学习一个回归Rt，使得θit =θit-1◦Rt（xi）最小化（4）中的损失。 经过一些操作，我们可以这样写：