算法的时间复杂度

时间复杂度

时间复杂度:我们将算法执行运算的操作数丢弃掉低阶项,再去掉所有的系数.

在它前面加上一个O,就是大O表示法.

int n = 100;
int a = 10;
System.out.println(a);
//总共执行3次

没有更低阶的项了,系数是3, 去掉系数3, 所以时间复杂度是 O(1)

        int n = 100;
        int a = 10; 
        for (int i = 0; i < n; i++) {  //n次
            System.out.println(a);     //n次
        }
        System.out.println(a);
        //总共执行2n + 3次

去掉低阶项3,再去掉系数2,所以它的时间复杂度就是O(n)

        int n = 100;
        int a = 10;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                System.out.println(a);
                System.out.println(a);
            }
        }
        System.out.println(a);
//2n^2+3次

去掉低阶项3,再去掉系数2, 所以它的时间复杂度是O(n²)

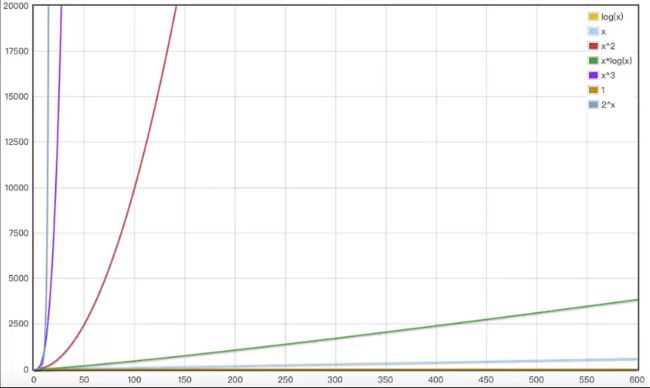
常见的时间复杂度

即使系数很大,但是对于我们来说都没有意义,只要n的数量级够大,总能抹平低阶项和系数带来的影响 , 高阶项才是函数增长的主要影响因素.

增长速度

一般法则

for循环

假设循环体的时间复杂度为O(n),循环次数为m,则这个循环的时间复杂度为O(m*n).

时间复杂度为O(n*1), 即O(n).

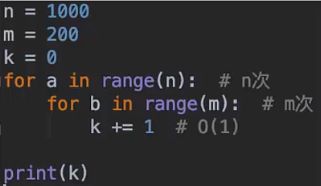
嵌套的for循环

对于多个循环,假设循环体的时间复杂度为O(n),各个循环的循环次数分别为a,b,c,则这个循环的时间复杂度为O(n*a*b*c…).

分析的时候应该从里向外分析这些循环.

时间复杂度为O(1*m*n), 即O(m*n)

顺序语句

各个语句的运行时间求和即可(或者说取最大值).

时间复杂度为O(2+n+n²+1),即为 O(n²).

分支语句

总的时间复杂度等于其中时间复杂度最大的路径的时间复杂度

这里如果运气好,第一次判断进入if就结束了,那么时间复杂度就是O(n),

但是算法的时间复杂度是按最坏的情况来算的,所以看时间复杂度最大的路径是怎样的,这才是最终的时间复杂度.

所以上图的时间复杂度为O(n²)

函数调用

for (int i = 0; i < n; i++) {  //O(n)
             list.insert(0,i);   //O(n)
     }

上面的insert语句的时间复杂度是O(n), 而不是O(1), 所以它的时间复杂度是O(n²).

函数调用要看函数体里面的时间复杂度.

注意:

• 算法的速度并不能简单的以执行时间作为衡量标准

大O表示法

<<算法导论>>里的定义:

对于给定的函数g(n) , 用O(g(n))来表示以下函数的集合:

O(g(n)) = {f(n) : 存在正常量c和n0 , 使得对所有n>=n0 , 有0<=f(n)<=cg(n)}.

我们使用O记号来给出函数的一个在常量因子内的上界.

大O表示法往往是表示最坏复杂度的.

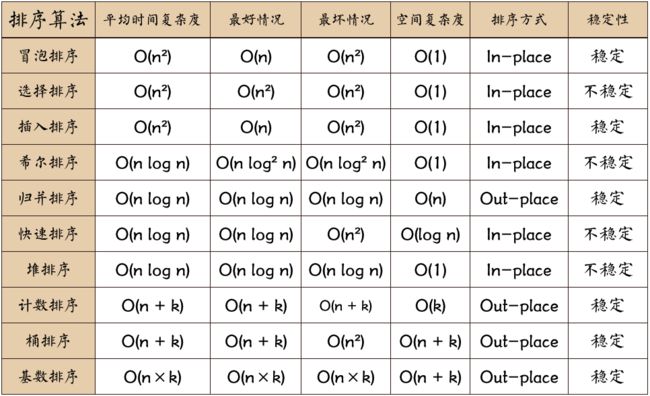
常见排序算法及其对应的时间复杂度和空间复杂度

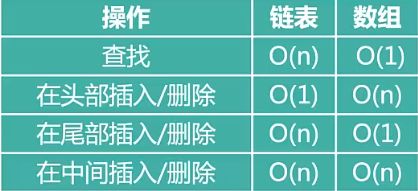
常见数据结构时间复杂度

查找

• 数组可以直接根据下标查询,所以是O(1)
• 链表必须一个一个的去找,所以是O(n)

头部插入/删除

• 数组需要把每个数据都向后移动,所以是O(n)
• 链表随意找一个位置放置元素,指针指向下一个即可,所以是O(1)

尾部插入/删除

• 数组直接定位到尾部,输入数据就可以(数组未满才可插入)
• 链表需要先遍历才能找到最后一个元素的位置,再进行插入

中间插入/删除

• 数组的时间用在了数据的拷贝,覆盖上面

• 链表的时间用在了遍历上面

数组和链表的选择

插入/删除很少,查询非常多,又不会 Out of memory ,采用数组.

如果是频繁的插入,遍历,查询检索很少,就采用链表.