人脸关键点: Wing Loss for Robust Facial Landmark Localisation with Convolutional Neural Networks

原文链接：https://blog.csdn.net/u011995719/article/details/80150508#commentsedit

Wing Loss for Robust Facial Landmark Localisation with Convolutional Neural Networks
由萨里大学研究人员（第一至四作者）与江南大学研究人员（第五作者）共同研究，被CVPR2018收录，最早于2017年11月在arXiv上发表(美[ˈɑ:rkaɪv]) ：
https://arxiv.org/abs/1711.06753v4

近几年，人脸关键点检测大多在“由粗到精”（coarse to fine）上研究，而这篇文章则另辟蹊径。依作者所说，这是第一篇在人脸关键点检测任务上对loss function进行讨论分析的文章，文章在loss function上进行改进，为人脸关键点检测任务提出“专用”的loss function——Wing loss，作者的出发点值得借鉴。

创新点：

1.针对人脸关键点检测提出新的loss function —— Wing Loss
2.针对人脸姿态角度多样而导致的检测精度不高问题，提出一种基于姿态的数据均衡方法，从而提升人脸姿态变化时的关键点检测精度，这也是文章题目中“Robust”的体现

主要工作：
除上述两点外，第三点是采用 two-stage landmark localisation，其实就是级联卷积神经网络的思想，更多人脸关键点检测中的级联思想可参见：
级联MobileNet-V2实现CelebA人脸关键点检测
深度学习人脸关键点检测方法—综述

我将从三个部分进行介绍这篇论文，分别是Wing loss、数据均衡方法 和 Two-stage landmark localisation，重点当然是Wing loss啦~~

Wing loss

命名：文中没有提到为什么命名为Wing loss，但是从 Wing loss的曲线图看到，好像翅膀（Wing），或许因此得名吧

Wing loss 公式如下：

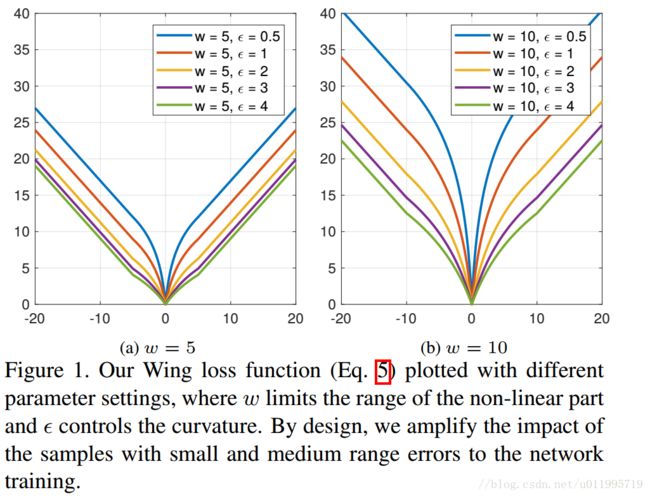
这里抛出两个问题：

第一，这是一个分段函数，为什么是分段函数？
第二，当$\left|x\right|<w$ 时，主体是一个对数函数，另外还有两个控制参数，分别是w和ε，为什么是对数函数？为什么要加控制参数？

先解释第二个问题，通常的人脸关键点检测任务（回归任务）loss function都采用L2、L1和smooth L1 ，其中L2是使用最为广泛的
这三个loss function曲线如下图所示：

作者是从L1和L2存在的问题出发，从而提出Wing loss的，那么L1和L2有什么问题呢？

从图中可知，L1和L2的gradient分别是1和$\left | x \right | $ ， optimal step size是$\left | x \right | $ 和1，并指出L1的gradient为常数，而step size会被large errors主导；L2的step size会被large errors主导，而gradient为常数。这样并不好（不知道为什么，看了几遍原文也没看明白，看明白的朋友可以解释一下么？）

从这里发现，在L1、L2中，对small errors并不“友好”，于是，作者认为换一种对small errors“友好”的function，例如lnx。 lnx的gradient为1/x，optimal step size为x平方，这样gradient就由small errors“主导”，step size由large errors“主导”。

这就解释了为什么 wing（x）的第一段 $wln（1+\left|x\right|/ϵ）,if\left|x\right|<w$. 的主体是对数函数。

但为了避免在错误的方向上“走”一大步，因此再small errors 时，需要gradient进行限制，本文就采用两个参数来控制gradient，分别是w和ε

解释第一个问题：为什么分段？

同样地，作者先分析常用loss function存在的问题，针对性的对其进行改善。对于L2 loss function，有一个众所周知的缺点，那就是对“离群点”敏感，即当某个点的预测值与真实值误差较大时，整个loss将由这个点所“主导”，在这里就提出问题loss function设计时的第一个问题，x较大时(large errors )，其函数值不应太大。而正是因为L2 loss function的这个缺点，已有研究人员采用smooth L1替换掉L2，获得更高的精度 [原文的参考文献22、45]

为了避免x较大时，其函数值过大，所以要将Wing loss分段，对于大的那一部分采用另外一个表达式，即：

wing(x) = $\left|x\right|-C,if\left|x\right|\ge w$

其中 $C = w − w ln(1 + w/\epsilon) $ 是一个常数，这个操作思想想必是来源于smooth L1 loss function的，看一下smooth L1 loss function表达式：

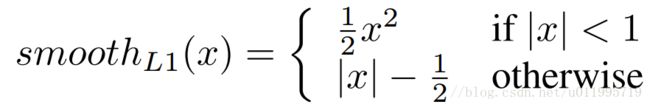
讲到这里，Wing loss的由来就讲完啦，但是最最关键的还是要调参。。。要找合适的 $w和ϵ$ ，作者做了一系列实验，给出了推荐值，请实验结果：

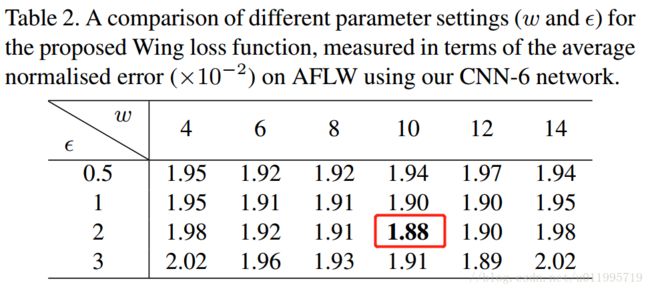
PBD（Pose-based Data Balancing）

本文除了提出一种新的loss function，还针对人脸关键点检测任务中遇到的人脸姿态多样化问题，提出一种基于姿态的数据均衡方法，来提升人脸关键点检测精度。

在分类任务中，数据不均衡非常容易导致模型性能不佳，而在人脸关键点任务（回归任务）中，作者同样认为，正脸太多，有旋转的脸太少，从而导致模型对有旋转的人脸的关键点检测精度低。 因此，提出一种基于姿态的数据均衡方法——PDB（Pose-based Data Balancing）

PDB方法：首先将 training shapes进行对齐，将对齐后的training shapes进行PCA，用shape eigenvector将original shapes进行投影至一维空间，用来控制姿态变化。整个训练集投影后的系数通过一个直方图来展示，如下图所示：

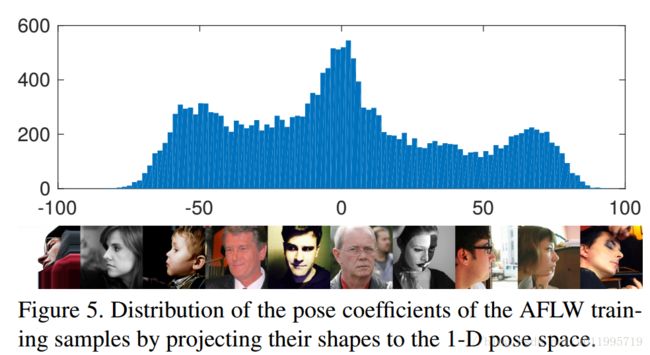
有了这个直方图，就可以看到哪些姿态的人脸图像多，哪些少，然后通过复制那些占比较少的样本，使得所有样本均衡，这就是PDB方法。实验结果表明PDB方法可以提升人脸关键点检测精度：

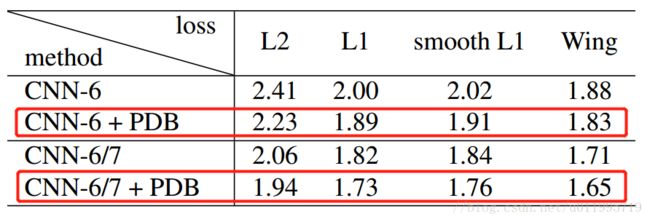
Two-stage landmark localisation（Pose-based Data Balancing）

为了进一步提升精度，作者采用了级联思想，在文中称之为 Two-stage landmark localisation

level-1 采用的是CNN-6，level-2采用的是CNN-7， CNN-7与CNN-6不同之处在于：

1. input比CNN-6大一倍，为1281283
2. 多了一组操作——卷积、池化
3. 第一个卷积层的卷积核个数为64（CNN-6为32）

level-1输出的landmark有两个作用：

1. 移除人脸角度；
2. 矫正bounding box 为level-2 提供更好的输入

CNN-6 模型如下：

小结

通过阅读该文章可知，在做人脸关键点时，可以注意以下几点：

1. 由于人脸关键点检测是特殊的回归任务，因而要注意loss function是否对每一个点都“友好”，选用不同的loss function尝试实验，或许有新发现

2. 数据不均衡问题不仅困扰分类任务，在人脸关键点检测任务中，不同姿态的人脸样本不均衡，同样会影响模型获得更高的精度，因此可尝试使用某一种指标，去衡量训练样本当中，人脸姿态的分布情况，然后对应的做数据均衡（该法数据数据增强）

3. 级联，利用上一级的output，对iamge进行裁剪，使下一级获得更好的input