九大内部排序算法（快速排序、归并排序、堆排序、希尔排序、基数排序）

排序（Sorting）是计算机程序设计中的一种重要操作，它的功能是将一个数据元素（或记录）的任意序列，重新排列成一个按关键字有序的序列。

---

• 内部排序，是指待排序列完全存放在内存中所进行的排序过程，适合不太大的元素序列。
• 外部排序，指的是大文件的排序，即待排序的记录存储在外存储器上，待排序的文件无法一次装入内存，需要在内存和外部存储器之间进行多次数据交换，以达到排序整个文件的目的。

九大内部排序：直接插入排序、折半插入排序、希尔排序、冒泡排序、快速排序、简单选择排序、堆排序、归并排序以及基数排序。

算法稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的。

注：事实上，基数排序不是基于比较的。

---

内部排序可分为五大类，插入排序、交换排序、选择排序、归并排序和基数排序。导图关系如下：

---

#1.直接插入排序

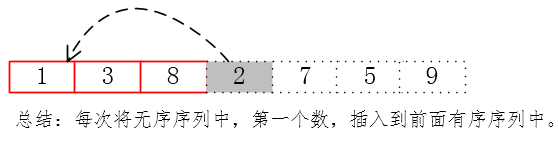
**直接插入排序（Straight Insertion Sort）**是一种最简单的排序方法，它的基本操作是将一个记录插入到已排好序的有序表中，从而得到一个新的、记录数增1的有序表。

void InsertSort(char A[], int n)
{
	int i,j;

	for (i = 2; i <= n; i++)
	{
		if (A[i] < A[i-1])
		{
			A[0] = A[i];     //复制为哨兵，A[0]不存放元素
			for (j = i-1; A[0] < A[j]; j--)    //从后往前查待插入位置
			{
				A[j+1] = A[j];
			}
			A[j+1] = A[0];
		}
	}
}

---

#2.折半插入排序

在直接插入排序基础上，对前面有序部分采用折半查找，减少了比较元素的次数。但有个要求，必须是顺序存储的线性表。

void InsertSort2(char A[], int n)
{
	int i,j,low,high,mid;

	for (i = 2; i <= n; i++)
	{
		A[0] = A[i];     
		low = 1; high = i-1;

		while (low <= high)    //折半查找
		{
			mid = (low+high)/2;

			if (A[mid] > A[0])
				high = mid-1;
			else
				low = mid+1;
		}

		for (j = i-1; j >= high+1; j--)    
		{
			A[j+1] = A[j];
		}

		A[high+1] = A[0];
	}
}

---

#3.希尔排序

**希尔排序（Shell’s Sort）**又称“缩小增量排序”，它是一种属于插入排序类的方法，但在时间效率上较前述几种算法有较大改进。

希尔排序的基本思想是：先将待排序表分割成若干个“特殊”子表，分别进行直接插入排序，当整个表中元素已呈现“基本有序”时，再对全体记录进行一次直接插入排序。希尔排序的分析是一个复杂的问题，因为它的时间是所取“增量”序列的函数，这涉及一些数学上尚未解决的难题。

注意：希尔排序最后一个增量一定等于1。

void ShellSort(char A[], int n)
{
	int i,j,dk;

	for (dk = n/2; dk >= 1; dk /= 2)  //dk是步长
	{
		for (i = dk+1; i <= n; ++i)
		{
			if (A[i] < A[i-dk])
			{
				A[0] = A[i];   //A[0]不使用，充当暂存器
				for (j = i-dk; j > 0 && A[0] < A[j]; j-=dk)
				{
					A[j+dk] = A[j];
				}
				A[j+dk] = A[0];
			}
		}
	}
}

---

#4.冒泡排序

冒泡排序（Bubble Sort），是一种计算机科学领域的较简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端，故名。

void BublleSort(char A[], int n)
{
	int i,j;
	bool flag;

	for (i = 0; i < n-1; i++)
	{
		flag = false;
		for (j = n-1; j > i; j--)
		{
			if (A[j-1] > A[j])
			{
				swap(A[j-1],A[j]);
				flag = true;
			}
		}
		if (!flag)
			return;
	}
}

---

#5.快速排序

**快速排序（Quicksort）**是对冒泡排序的一种改进。快速排序由C. A. R. Hoare在1962年提出。

它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

//划分——每次划分唯一确定一个元素位置
int Partition(int A[], int low, int high)
{
	int pivot = A[low];  //一般采用严蔚敏教材版本，以第一个位置为基准

	while (low < high)
	{
		while (low < high && A[high] >= pivot)
		{
			--high;
		}
		A[low] = A[high];  //将比基准小的元素移动到左端

		while (low < high && A[low] <= pivot)
		{
			++low;
		}
		A[high] = A[low];  //将比基准小的元素移动到右端
	}
	A[low] = pivot;

	return low;
}

//快排——平均时间复杂度O(log2n)
void QuickSort(int A[], int low, int high)
{
	int pivotpos;

	if (low < high)
	{
		pivotpos = Partition(A,low,high);
		//依次对划分后的子表递归排序
		QuickSort(A,low,pivotpos-1);
		QuickSort(A,pivotpos+1,high);
	}
}

---

#6.简单选择排序

设所排序序列的记录个数为n。i取1,2,…,n-1,从所有n-i+1个记录（Ri,Ri+1,…,Rn）中找出排序码最小的记录，与第i个记录交换。执行n-1趟 后就完成了记录序列的排序。

void swap(char &a, char &b)
{
	char t = a;
	a = b;
	b = t;
}

void SelectSort(char A[], int n)
{
	int i,j,min;

	for (i = 0; i < n-1; i++)
	{
		min = i;
		for (j = i+1; j < n; j++)
		{
			if (A[j] < A[min])
				min = j;
		}
		if (min != i)
			swap(A[i],A[min]);
	}
}

---

#7.堆排序

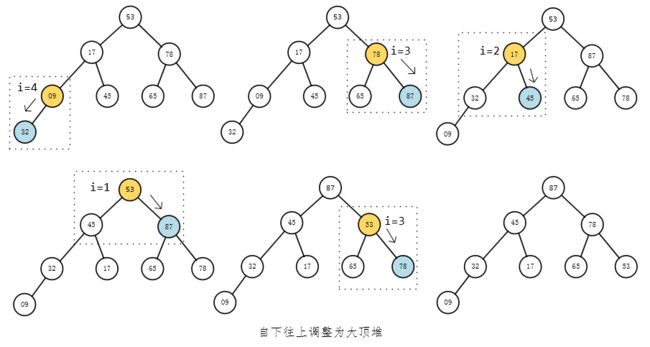
**堆排序(Heapsort)**是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆，是完全二叉树。大根堆的要求是每个节点的值都不大于其父节点的值，即A[parent[i]] >= A[i]。在数组的非降序排序中，需要使用的就是大根堆，因为根据大根堆的要求可知，最大的值一定在堆顶。

//向下调整堆
void AdjustDown(char A[], int k, int len)
{
	int i;
	
	A[0] = A[k];
	for (i = 2*k; i <= len; i*=2)
	{
		if (i < len && A[i] < A[i+1])
			i++;
		if (A[0] >= A[i])
			break;
		else
		{
			A[k] = A[i];
			k = i;
		}
	}
	A[k] = A[0];
}

//创建大顶堆
void BuildMaxHeap(char A[], int len)
{
	int i;

	for (i = len/2; i > 0; i--)  //调整堆
		AdjustDown(A,i,len);
}

//交换两数
void swap(char &a, char &b)
{
	char t = a;
	a = b;
	b = t;
}
//char A[] = " abfced";
//HeapSort(A,strlen(A)-1);
//堆排序
void HeapSort(char A[], int len)
{
	int i;

	BuildMaxHeap(A,len);  //创建初始堆
	for (i = len; i > 1; i--)  //把最大值顶到堆顶，再与堆底交换
	{
		swap(A[i],A[1]);
		AdjustDown(A,1,i-1);
	}
}

---

#8.归并排序

**归并排序（Merge Sort）**是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

char A[] = "badcgef";
char *B = (char*)malloc((strlen(A)+1)*sizeof(char));
//将A[low...mid]、A[mid+1...high]合并为一个表，合并前A两子表有序
void Merge(char A[], int low, int mid, int high)
{
	int i,j,k;

	for (k = low; k <= high; k++) //将A全部复制到B中
		B[k] = A[k];
	for (i = low, j = mid+1, k = i; i <= mid && j <= high; k++)
	{
		if (B[i] <= B[j])
			A[k] = B[i++];
		else
			A[k] = B[j++];
	}
	while (i <= mid)   //复制未检测完表
		A[k++] = B[i++];
	while (j <= high)
		A[k++] = B[j++];
}
//归并排序
void MergeSort(char A[], int low, int high)
{
	if (low < high)
	{
		int mid = (low + high)/2;
		MergeSort(A,low,mid);
		MergeSort(A,mid+1,high);
		Merge(A,low,mid,high);
	}
}

---

#9.基数排序

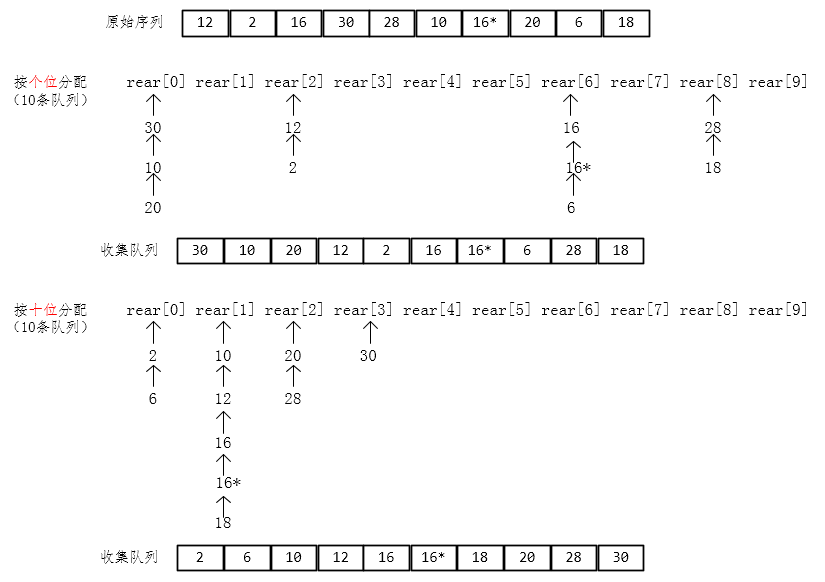
**基数排序（Radix Sort）**它不是基于比较进行排序的，而是采用多关键字排序思想，借助“分配”和“收集”两种操作对单逻辑关键字进行排序。基数排序又分为最高位优先（MSD）排序和最低位优先（LSD）排序。

---

#附1：各种内部排序算法性质

---

参考文献
[1] 王道论坛. 数据结构联考复习指导[M]. 北京:电子工业出版社, 2016.
[2] 严蔚敏, 吴伟民. 数据结构（C语言版）[M]. 北京:清华大学出版社, 2015.