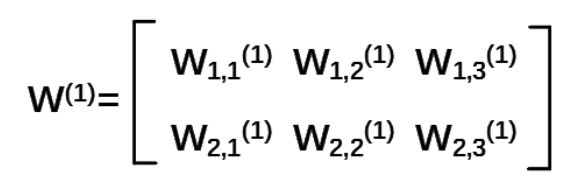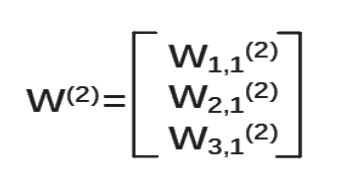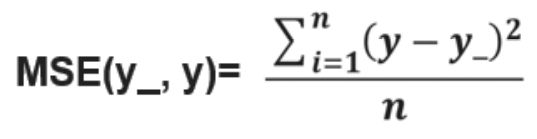Tensorflow学习:搭建神经网络
原文链接:https://www.cnblogs.com/wanyu416/p/9009985.html
一、神经网络的实现过程
1、准备数据集,提取特征,作为输入喂给神经网络
2、搭建神经网络结构,从输入到输出
3、大量特征数据喂给 NN,迭代优化 NN 参数
4、使用训练好的模型预测和分类
二、前向传播
前向传播就是搭建模型的计算过程,可以针对一组输入给出相应的输出。
举例:假如生产一批零件, 体积为 x1, 重量为 x2, 体积和重量就是我们选择的特征,把它们喂入神经网络, 当体积和重量这组数据走过神经网络后会得到一个输出。
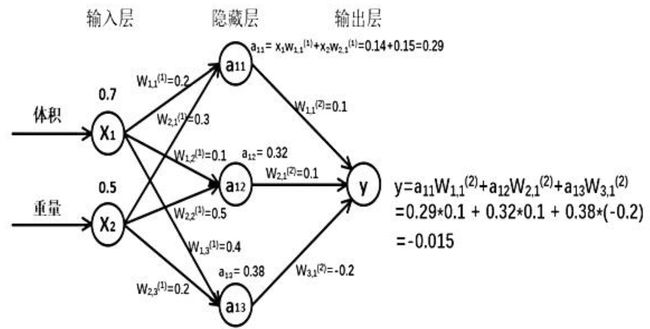
假如输入的特征值是:体积 0.7 ,重量 0.5 ,下图是搭建的神经网络框架图
由搭建的神经网络可得, 隐藏层节点 a11=x1* w11+x2*w21=0.14+0.15=0.29, 同理算得节点 a12=0.32, a13=0.38,最终计算得到输出层 Y=-0.015, 这便实现了前向传播过程。
再来推导图中的代码实现过程。
第一层:
(1)x是输入为1*2的矩阵:用x表示输入,是一个1行2列的矩阵,表示一次输入一组特征,这组特征包含了体积和重量两个元素。
(2)W前节点编号,后节点编号(层数)为待优化的参数:前面两个节点,后面三个节点。所以w应该是个两行三列的矩阵。表示为
注意:神经网络共有几层是指计算层, 输入不算作计算层,所以 上图中a 为第一层网络,a 是一个一行三列矩阵。
第二层:
(1)参数要满足前面三个节点,后面一个节点,所以W(2)是三行一列矩阵。表示为
我们把每层输入乘以线上的权重w,这样就可以用矩阵乘法输出y了。
下面讨论这其中的细节问题。
1、神经网络的参数
显然权重w是很重要的参数,我们刚开始设置w变量的时候,一般会先随机生成这些参数,当然肯定是变量形式。
所以这里介绍一下 tf 常用的生成随机数/数组的函数:
(1)tf.random_normal() 生成正态分布随机数
w=tf.Variable(tf.random_normal([2,3],stddev=2, mean=0, seed=1))
# 表示生成正态分布随机数,形状两行三列,标准差是2,均值是0,随机种子是1(2)tf.truncated_normal() 生成去掉过大偏离点的正态分布随机数,也就是如果随机生成的数据偏离平均值超过两个标准差,这个数据将重新生成
w=tf.Variable(tf.Truncated_normal([2,3],stddev=2, mean=0, seed=1))3)tf.random_uniform() 生成均匀分布随机数
w=tf.Variable(tf.random_uniform([2,3],minval=0,maxval=1,dtype=tf.float32,seed=1))
# 表示从一个均匀分布[minval maxval)中随机采样,产生的数是均匀分布的,注意定义域是左闭右开,即包含 minval,不包含 maxval。以上这些函数,如果没有特殊要求标准差、 均值、 随机种子是可以不写的。看具体使用情况。
(4)其它函数:tf.zeros 表示生成全 0 数组
tf.ones 表示生成全 1 数组
tf.fill 表示生成全定值数组
tf.constant 表示生成直接给定值的数组
tf.zeros([3,2],int32) # 表示生成[[0,0],[0,0],[0,0]]
tf.ones([3,2],int32) # 表示生成[[1,1],[1,1],[1,1]
tf.fill([3,2],6) # 表示生成[[6,6],[6,6],[6,6]]
tf.constant([3,2,1]) # 表示生成[3,2,1]2、placeholder占位,输入多组数据
不做赘述,直接在代码里面注释这样的操作
细节讨论完,下面就是用代码实现前向传播
# (1) 用placeholder 实现输入定义(sess.run 中喂入一组数据)的情况,特征有体积和重量,数据为体积 0.7、重量 0.5
import tensorflow as tf
x = tf.placeholder(tf.float32,shape=(1,2)) # placeholder占位,首先要指定数据类型,然后可以指定形状,因为我们现在只需要占一组数据,且有两个特征值,所以shape为(1,2)
w1 = tf.Variable(tf.random_normal([2,3],stddev=1,seed=1)) # 生成权重
w2 = tf.Variable(tf.random_normal([3,1],stddev=1,seed=1))
a = tf.matmul(x,w1) # 矩阵乘法op
y = tf.matmul(a,w2)
with tf.Session() as sess:
init = tf.global_variables_initializer() # 初始化以后就放在这里,不容易忘记
sess.run(init)
print("y is",sess.run(y,feed_dict={x:[[0.7,0.5]]})) # 以字典形式给feed_dict赋值,赋的是一个一行两列的矩阵,注意张量的阶数。这里只执行了y的op,因为执行了y也就执行了a这个op运行显示结果为:
y is: [[ 3.0904665]]# (2) 用 placeholder 实现输入定义(sess.run 中喂入多组数据)的情况
import tensorflow as tf
#定义输入和参数
x=tf.placeholder(tf.float32,shape=(None,2)) # 这里占位因为不知道要输入多少组数据,但还是两个特征,所以shape=(None,2),注意大小写
w1=tf.Variable(tf.random_normal([2,3],stddev=1,seed=1))
w2=tf.Variable(tf.random_normal([3,1],stddev=1,seed=1))
#定义前向传播过程
a=tf.matmul(x,w1)
y=tf.matmul(a,w2)
#用会话计算结果
with tf.Session() as sess:
init_op=tf.global_variables_initializer()
sess.run(init_op)
print("y is:",sess.run(y,feed_dict={x:[[0.7,0.5],
[0.2,0.3],
[0.3,0.4],
[0.4,0.5]]})) # 输入数据,4行2列的矩阵运行显示结果为:
y is: [[ 3.0904665 ]
[ 1.2236414 ]
[ 1.72707319]
[ 2.23050475]]以上就是最简单的神经网络前向传播过程。
三、后向传播
反向传播:训练模型参数,以减小loss值为目的,使用优化方法,使得 NN 模型在训练数据上的损失函数最小。
损失函数(loss): 计算得到的预测值 y 与已知答案 y_ 的差距。损失函数的计算有很多方法,均方误差( MSE) 是比较常用的方法之一。
均方误差 MSE: 求前向传播计算结果与已知答案之差的平方再求平均。
用tensorflow函数表示为:loss_mse = tf.reduce_mean(tf.square(y_ - y))
反向传播训练方法: 以减小 loss 值为优化目标。
一般有梯度下降、 momentum 优化器、 adam 优化器等优化方法。这三种优化方法用 tensorflow 的函数可以表示为:
train_step=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
train_step=tf.train.MomentumOptimizer(learning_rate, momentum).minimize(loss)
train_step=tf.train.AdamOptimizer(learning_rate).minimize(loss)
三种优化方法的区别:
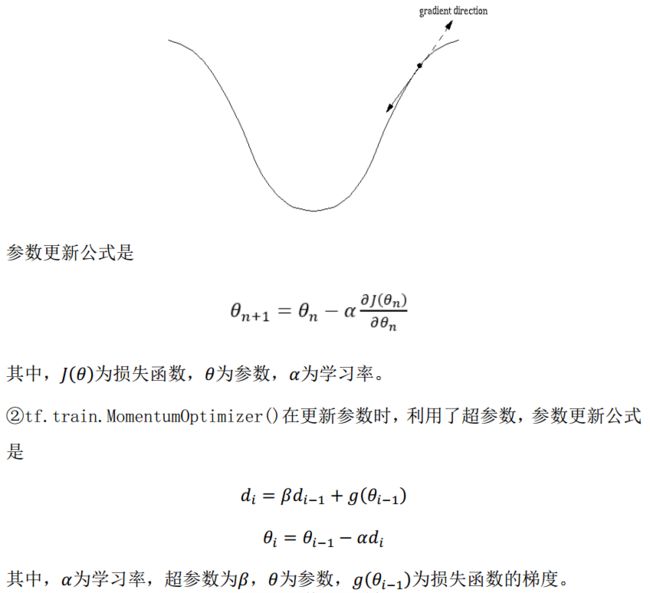
学习率:决定每次参数更新的幅度。
优化器中都需要一个叫做学习率的参数,使用时,如果学习率选择过大会出现震荡不收敛的情况(步子跨的太大),如果学习率选择过小,会出现收敛速度慢的情况。我们可以选个比较小的值填入,比如 0.01、0.001。
Python代码实现加上反向传播的NN:
随机产生 32 组生产出的零件的体积和重量,训练 3000 轮,每 500 轮输出一次损失函数。
import tensorflow as tf
import numpy as np
BATCH_SIZE = 8 # 一次输入网络的数据,称为batch。一次不能喂太多数据
SEED = 23455 # 产生统一的随机数
# 基于seed产生随机数,这是根据随机种子产生随机数的一种常用方法,要熟练运用
rdm = np.random.RandomState(SEED)
# 随机数返回32行2列的矩阵 表示32组 体积和重量 作为输入数据集。因为这里没用真实的数据集,所以这样操作。
X = rdm.rand(32, 2)
# 从X这个32行2列的矩阵中 取出一行 判断如果和小于1 给Y赋值1 如果和不小于1 给Y赋值0 (这里只是人为的定义),作为输入数据集的标签(正确答案)
Y_ = [[int(x0 + x1 < 1)] for (x0, x1) in X]
print("X:\n", X)
print("Y_:\n",Y_)
# 1定义神经网络的输入、参数和输出,定义前向传播过程。
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)
# 2定义损失函数及反向传播方法。
loss = tf.reduce_mean(tf.square(y - y_))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss) # 三种优化方法选择一个就可以
# train_step = tf.train.MomentumOptimizer(0.001,0.9).minimize(loss_mse)
# train_step = tf.train.AdamOptimizer(0.001).minimize(loss_mse)
# 3生成会话,训练STEPS轮
with tf.Session() as sess:
init = tf.global_variables_initializer()
sess.run(init)
# 输出目前(未经训练)的参数取值。
print("w1:\n", sess.run(w1))
print("w2:\n", sess.run(w2))
print("\n")
# 训练模型。
STEPS = 3000
for i in range(STEPS): #0-2999
start = (i * BATCH_SIZE) % 32 #i=0,start=0,end=8;i=1,start=8,end=16;i=2,start=16,end=24;i=3,start=24,end=32;i=4,start=0,end=8。也就是说每次训练8组数据,一共训练3000次。
end = start + BATCH_SIZE
sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]})
if i % 500 == 0:
total_loss = sess.run(loss, feed_dict={x: X, y_: Y_})
print("After %d training step(s), loss on all data is %g"%(i,total_loss))
# 输出训练后的参数取值。
print("\n")
print("w1:\n", sess.run(w1))
print("w2:\n", sess.run(w2))运行显示结果为
X:
[[ 0.83494319 0.11482951]
[ 0.66899751 0.46594987]
[ 0.60181666 0.58838408]
[ 0.31836656 0.20502072]
[ 0.87043944 0.02679395]
[ 0.41539811 0.43938369]
[ 0.68635684 0.24833404]
[ 0.97315228 0.68541849]
[ 0.03081617 0.89479913]
[ 0.24665715 0.28584862]
[ 0.31375667 0.47718349]
[ 0.56689254 0.77079148]
[ 0.7321604 0.35828963]
[ 0.15724842 0.94294584]
[ 0.34933722 0.84634483]
[ 0.50304053 0.81299619]
[ 0.23869886 0.9895604 ]
[ 0.4636501 0.32531094]
[ 0.36510487 0.97365522]
[ 0.73350238 0.83833013]
[ 0.61810158 0.12580353]
[ 0.59274817 0.18779828]
[ 0.87150299 0.34679501]
[ 0.25883219 0.50002932]
[ 0.75690948 0.83429824]
[ 0.29316649 0.05646578]
[ 0.10409134 0.88235166]
[ 0.06727785 0.57784761]
[ 0.38492705 0.48384792]
[ 0.69234428 0.19687348]
[ 0.42783492 0.73416985]
[ 0.09696069 0.04883936]]
Y_:
[[1], [0], [0], [1], [1], [1], [1], [0], [1], [1], [1], [0], [0], [0], [0], [0], [0], [1], [0], [0], [1], [1], [0], [1], [0], [1], [1], [1], [1], [1], [0], [1]]
w1:
[[-0.81131822 1.48459876 0.06532937]
[-2.4427042 0.0992484 0.59122431]]
w2:
[[-0.81131822]
[ 1.48459876]
[ 0.06532937]]
After 0 training step(s), loss_mse on all data is 5.13118
After 500 training step(s), loss_mse on all data is 0.429111
After 1000 training step(s), loss_mse on all data is 0.409789
After 1500 training step(s), loss_mse on all data is 0.399923
After 2000 training step(s), loss_mse on all data is 0.394146
After 2500 training step(s), loss_mse on all data is 0.390597
w1:
[[-0.70006633 0.9136318 0.08953571]
[-2.3402493 -0.14641267 0.58823055]]
w2:
[[-0.06024267]
[ 0.91956186]
[-0.0682071 ]]由神经网络的实现结果,我们可以看出,总共训练3000轮,每轮从X的数据集和Y的标签中抽取相对应的从start开始到end结束个特征值和标签,喂入神经网络,用sess.run求出loss,每500轮打印一次loss值。经过3000轮后,我们打印出最终训练好的参数w1、w2。
针对上面的代码,做出如下思考。首先最终的目的是使得loss值减小,那么:
1、如果增大训练次数,loss会不会继续减小?如果减小,会不会一直在减小?
2、如果增大学习率,loss会不会继续减小?如果减小,会不会一直在减小?
3、如果不用随机梯度下降算法,换用其他的优化器,会产生什么样的变化?
4、更改batch的值,会不会对结果有影响?
四、搭建神经网络的过程
通过以上的内容,我们可以梳理一下搭建简单神经网络的步骤:
(1)导入模块,生成模拟数据集
import
常量定义
生成数据集
(2)前向传播:定义输入、参数和输出
x= y_=
w1= w2=
a= y=
(3)后向传播:定义损失函数、反向传播方法
loss=
train_step=
(4)生成会话,训练STEPS轮
with tf.Session as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
STEPS =
for i in range(STEPS):
start =
end =
sess.run(train_step, feed_dict={ })