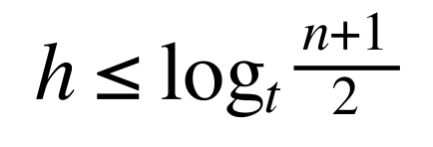《算法导论》第18章 B树
源码地址
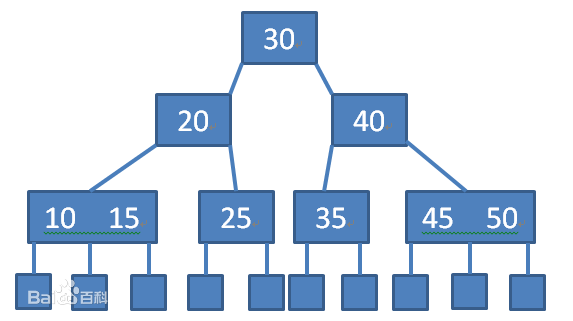
1. B树的定义
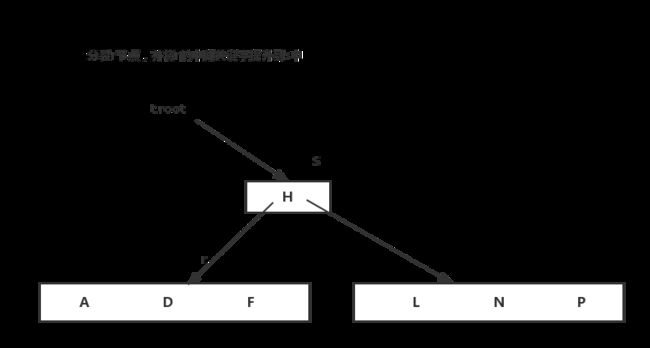
B树示意图:
// 保存在B树中的关键字,同时也可以保存其他数据
type Key interface {
CompareTo(other Key) int
String() string
}
type BTree struct {
root *BTreeNode
t int // 最小度数,除根节点外的内部节点至少有t个孩子,至多2t个孩子
}
type BTreeNode struct {
keys []Key // 关键字
children []*BTreeNode // 孩子节点
isLeaf bool // 是否是叶子节点
}- 关键字是以升序排列的(k[0] <= k[1] <= … <= k[n-1])
关键字和子结点的关系
NODE1的关键字都比k1小或等于,NODE2的关键字介于k1和k2之间,NODE3的关键字介于k2和k3之间,NODE4的关键字大于k3。
关键字的个数用树的最小度数t来衡量,除根节点外的结点最少t-1个关键字,最多2t-1个,相对应的,除根节点外的结点最少t个孩子,最多2t个。
关键字达到2t-1个时称该结点是满的。
每个叶子结点都有相同的深度,即树高h。
如果n(关键字个数)>=1,对任意一个包含n个关键字,高度为h,最小度数t>=2的B树:
h从0开始计算
2. B树上的操作
2.1 插入关键字
如果一个节点是满的(关键字个数为2*t-1个),此时就不能再插入了,所以引入一个分裂节点的操作,将一个满节点从中间分裂为两个,将中间的关键字提升到父节点中,分裂后的两个节点各有t-1个关键字。
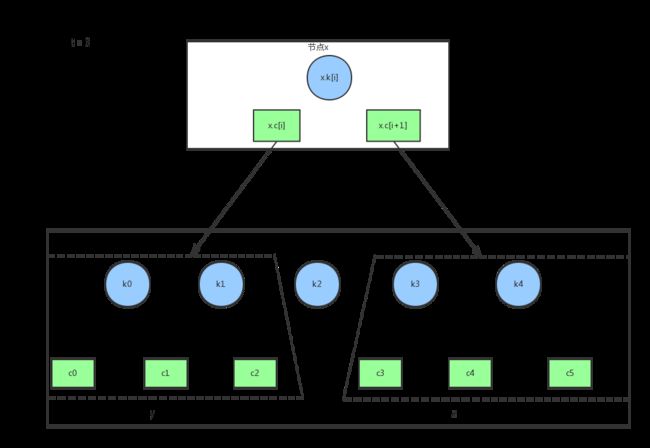
2.1.1 分裂满节点
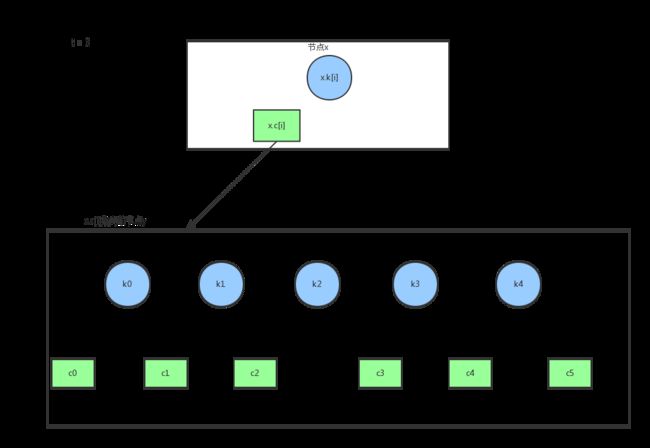
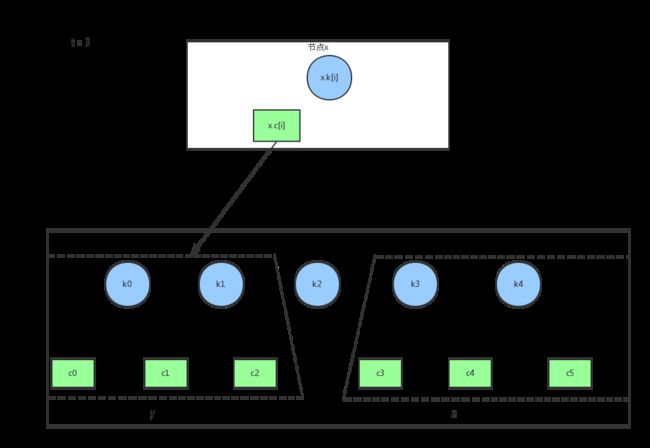
假设t==3, x.child[i]指向的节点是一个满节点:
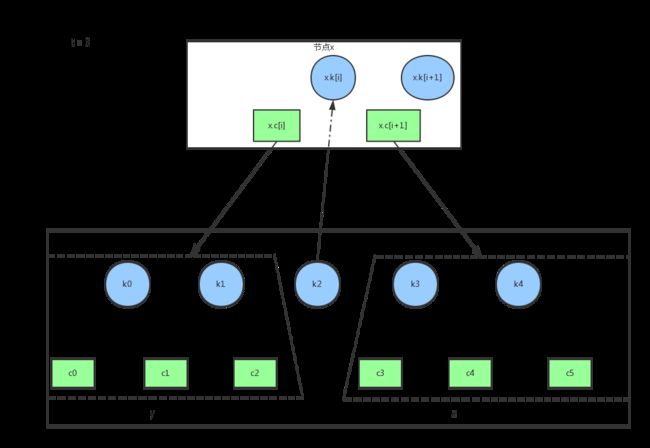
将y节点分裂成两个,y和z,各有t-1个关键字和t个子节点
将z节点当做x的第i+1个子节点,原来的child[i+1]及之后的子节点依次后移
将中间关键字k2当做x的keys[i],原来的keys[i]及之后的关键字依次后移
相关代码:
// splitChild分裂x的第i个子节点,x是非满的内部节点,x的children[i]已满,现在要分裂children[i]节点
func (t *BTree) splitChild(x *BTreeNode, i int) {
z := t.allocateNode() // 分裂出来的节点
y := x.children[i] // z将是y的兄弟节点
z.isLeaf = y.isLeaf
d := t.t
// y后半部分关键字分给z
// y和z各有d-1个关键字,y为keys[0..d-1),z为keys[d,2d-1),keys[d-1]被提到父节点中
for j := d; j < 2*d-1; j++ {
z.keys = append(z.keys, y.keys[j])
}
upKey := y.keys[d-1] // 将要提升的关键字
y.keys = y.keys[0 : d-1]
// 如果y不是叶子,将y后半部分的孩子节点也分给z,分t个
if !y.isLeaf {
for j := d; j < 2*d; j++ {
z.children = append(z.children, y.children[j])
}
y.children = y.children[0:d]
}
// 将z插入到x.children中
// y是x.children[i],那么z现在是x.children[i+1]
x.children = append(x.children, nil)
for j := len(x.children) - 1; j > i+1; j-- {
// x有n个关键字,必然有n+1个子结点
x.children[j] = x.children[j-1]
}
x.children[i+1] = z
// 将提升上来的关键字插入到x.keys中
// 分裂前y中所有关键字都比x.keys[i]小,分裂后提升上来的关键字也比x.keys[i]小,所以插入到x.keys[i]之前
x.keys = append(x.keys, nil)
for j := len(x.keys) - 1; j >= i+1; j-- {
x.keys[j] = x.keys[j-1]
}
x.keys[i] = upKey
t.diskWrite(y)
t.diskWrite(z)
t.diskWrite(x)
}2.1.2 插入关键字
先上代码:
// Insert插入key
func (t *BTree) Insert(key Key) {
r := t.root
if len(r.keys) == 2*t.t-1 { // 根节点满了
s := t.allocateNode() // 新的根节点
t.root = s
s.isLeaf = false
s.children = append(s.children, r)
t.splitChild(s, 0) // 分裂r
t.insertNotFull(s, key)
} else {
t.insertNotFull(r, key)
}
}
// insertNotFull: 将k插入到x中,x不满。
func (t *BTree) insertNotFull(x *BTreeNode, k Key) {
i := len(x.keys) - 1
if x.isLeaf {
x.keys = append(x.keys, nil)
// 从后向前遍历,找到第一个小于或等于k的位置,将k插入到该位置后
for ; i >= 0 && k.CompareTo(x.keys[i]) < 0; i-- {
x.keys[i+1] = x.keys[i]
}
x.keys[i+1] = k
t.diskWrite(x)
} else {
// 从后向前遍历,找到第一个小于或等于k的位置
for ; i >= 0 && k.CompareTo(x.keys[i]) < 0; i-- {
}
i++
t.diskRead(x.children[i])
if len(x.children[i].keys) == 2*t.t-1 { // 满节点
t.splitChild(x, i)
// 分裂后x.keys[i]已经被替换成提升上来的那个关键字
if k.CompareTo(x.keys[i]) > 0 {
i++
}
}
t.insertNotFull(x.children[i], k) // 尾递归,可优化
}
}从树根向下遍历时每遇到一个满节点都分裂成两个节点,这样再插入新关键字时就可以保证父节点是不满的,就不需要再回溯了。
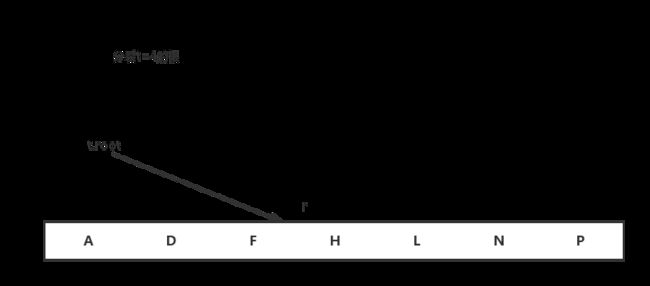
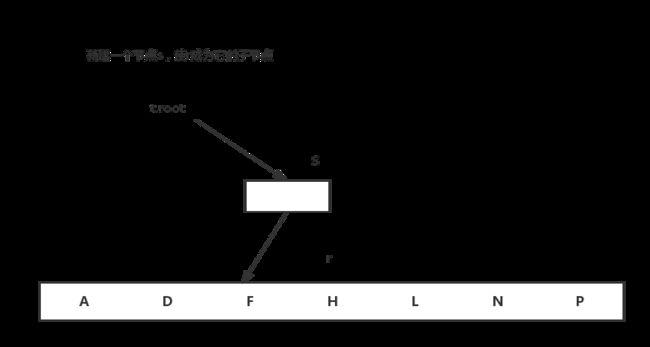
首先判断root指向的节点是不是满的,如果是,将root指向的节点一分为二,并用新的节点替代root,使树高增1.
insertNotFull 是在确保x为不满时调用的,首先检查x是不是叶子节点,如果是,将x插入到正确的位置。否则,先查找下一个需要下降的子节点,如果下降到一个满节点上,先将满节点分裂,然后递归调用insertNotFull处理。
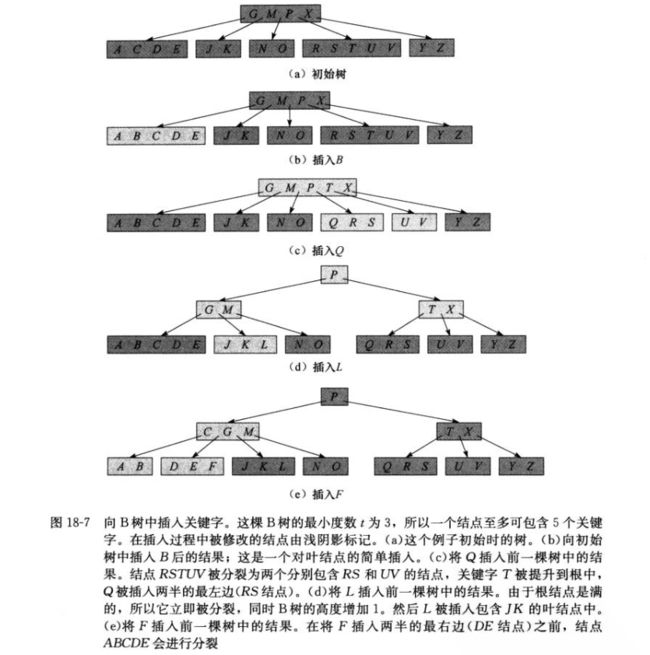
下面是算法导论上一个插入的例子:
2.2 删除关键字
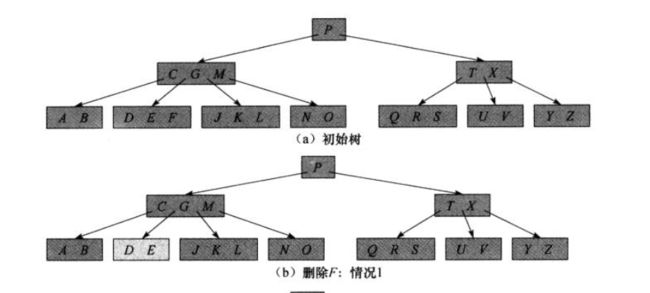
情况1:如果关键字在x中,并且x是叶子节点,则从x中删除k
如果 x 是根节点并且也是叶子节点,那么删除 k 后即使关键字个数没有达到 t-1 个,也不违反 B 树的性质。
如果 x 是叶子节点, 但不是根节点,那么在从根下降到 x 的过程中,应该保证 x 的关键字个数至少为 t 个,这样的话,x 在删除了一个关键字的情况下依然保证了关键字的个数不少于 t-1 个,这样在一趟下降的过程中就可以删除关键字k,而不需要回溯。
代码:
func (t *BTree) Delete(root *BTreeNode, k Key) {
if root == nil {
root = t.root
}
firstBig, compResult := root.notLessThan(k)
// 关键字在root中
if firstBig >= 0 && compResult == 0 {
// 情况1:如果关键字在root中,并且root是叶子节点,则从root中删除k
if root.isLeaf {
root.deleteKeyAt(firstBig)
return
}
} else if firstBig >= 0 { // 关键字不在 root 中,但在 root 的某个子节点中
// 递归删除
t.Delete(root.children[firstBig], k)
}
}
// notLessThan 返回this节点中第一个不小于k的关键字所在的下标,并且返回keys[index]和k比较的结果。
// 如果this节点中所有关键字都比k小,返回-1, -1
func (this *BTreeNode) notLessThan(k Key) (index int, compResult int) {
for i, n := 0, len(this.keys); i < n; i++ {
if comp := this.keys[i].CompareTo(k); comp >= 0 {
return i, comp
}
}
return -1, -1
}
// deleteKeyAt 删除下标为 index 的关键字
func (this *BTreeNode) deleteKeyAt(index int) {
len := len(this.keys)
if len <= 0 || index < 0 || index >= len {
return
}
if index == 0 {
this.keys = this.keys[1:]
return
}
if index == len-1 {
this.keys = this.keys[:len-1]
return
}
this.keys = append(this.keys[:index], this.keys[index+1:]...)
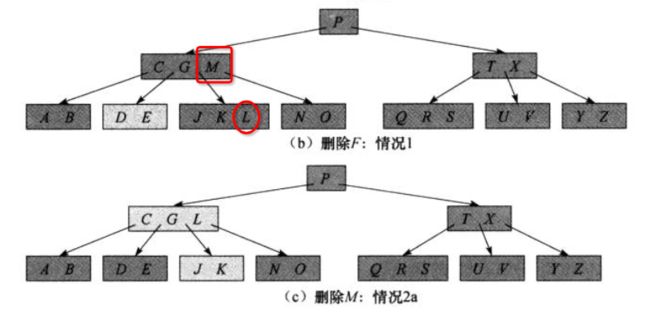
}情况2:如果关键字在x中,但x不是叶子节点
2.a 如果 x 中前于 k 的子节点 y 至少包含 t 个关键字,则找出 k 在以 y 为根的子树中的前驱 k’,递归的删除 k’,并在 x 中用 k’ 代替 k。
func (t *BTree) Delete(root *BTreeNode, k Key) {
if root == nil {
root = t.root
}
firstBig, compResult := root.notLessThan(k)
// 关键字在root中
if firstBig >= 0 && compResult == 0 {
// 情况1:如果关键字在root中,并且root是叶子节点,则从root中删除k
if root.isLeaf {
root.deleteKeyAt(firstBig)
return
}
// 情况2:如果关键字在root中,但root不是叶子节点
// y是关键字k之前的结点,即小于k的最大孩子
y := root.children[firstBig]
// z是关键字k之后的结点,即大于k的最小孩子
// z := root.children[firstBig+1]
// 情况[2.a]:root中前于k的子结点y包含至少t个关键字
if len(y.keys) >= t.t {
// 找出k在以y为根的子树中的前驱pre
pre := t.predecessor(y)
// 用前驱取代k
k = pre.keys[len(pre.keys)-1]
root.keys[firstBig] = k
// 递归地删除k
t.Delete(y, k)
return
}
} else if firstBig >= 0 { // 关键字不在 root 中,但在 root 的某个子节点中
// 递归删除
t.Delete(root.children[firstBig], k)
}
}
// 寻找以x为根的子树的前驱
func (t *BTree) predecessor(x *BTreeNode) *BTreeNode {
for !x.isLeaf {
x = x.children[len(x.keys)]
}
return x
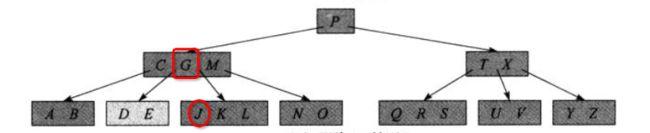
}2.b 如果 y 有少于 t 个关键字,则检查 x 中后于 k 的子节点 z,如果 z 至少有 t 个关键字,则找出 k 在以 z 为根的子树中的后继 k’,递归的删除 k’,并在 x 中用 k’ 代替 k.
删除 G 时,将使用 J 来取代 G。
// 情况2:如果关键字在root中,但root不是叶子节点
// y是关键字k之前的结点,即小于k的最大孩子
y := root.children[firstBig]
// z是关键字k之后的结点,即大于k的最小孩子
z := root.children[firstBig+1]
// 情况[2.a]:root中前于k的子结点y包含至少t个关键字
if len(y.keys) >= t.t {
// 找出k在以y为根的子树中的前驱pre
pre := t.predecessor(y)
// 用前驱取代k
k = pre.keys[len(pre.keys)-1]
root.keys[firstBig] = k
// 递归地删除k
t.Delete(y, k)
return
}
// 情况[2.b]: y少于t个关键字,但z至少t个关键字
if len(z.keys) >= t.t {
// 查找后继
next := t.successor(z)
// 用后继替换k
k = next.keys[0]
root.keys[firstBig] = k
// 递归删除k
t.Delete(z, k)
return
}
// 查找以x为根的子树的后继
func (t *BTree) successor(x *BTreeNode) *BTreeNode {
for !x.isLeaf {
x = x.children[0]
}
return x
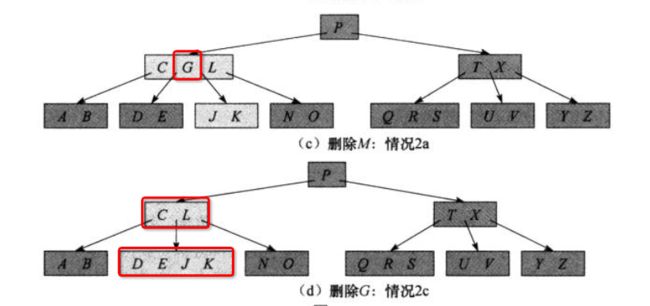
}2.c 否则,如果 y 和 z 都只含有 t-1 个关键字,则将 k 和 z 的全部合并进 y,y 现在包含 2t-1 个关键字,递归的从 y 中删除 k.
// 情况[2.c]:y和z都只有t-1个关键字,将k和z中所有关键字合并进y,使得x失去k和指向z的指针
// 将k关键字合并进y
y.keys = append(y.keys, k)
root.deleteKeyAt(firstBig)
// 将z合并到y
t.merge(y, z)
root.deleteChildAt(firstBig + 1)
// 如果root是树的根结点并且没有关键字了,替换根节点
if root == t.root && len(root.keys) == 0 {
t.root = y
}
// 将k从y中递归删除
t.Delete(y, k)情况3:关键字 k 不在内部节点 x 中
不在 x 中,则需要到 x 的下标为 i 的子树中查找(i 是大于 k 的最小的关键字的下标),在下降到子树前,需要确保子树的关键字个数至少为 t 个,如果小于 t 个,一旦在子树中删除了关键字,那么子树的关键字个数就不能保证至少 t-1 个了,违反了 B 树性质。
3.a 如果子树中只含有 t-1 个关键字,但某个相邻的兄弟节点至少包含 t 个关键字
以下面这棵树为例:
现在要删除 B ,如果直接删除的话那么 B 所在的节点的关键字个数就不满足至少 t-1 个了(t = 3),所以需要从相邻的兄弟节点中借一个关键字。EJK所在节点的关键字个数多于 t-1 个,可以借过来一个 E 。但如果直接将 E 放到 AB 所在节点,那么父节点中的 C 关键字就不满足大于它左边子树中的所有关键字了。所以,需要将 C 放到 AB 所在节点,然后将 E 上升到 C 原来的位置。
同样地,如果要删除 U,应该用 S 替换 T,将 T 下降到 UV 前形成 TUV。
// 情况3:y只有t-1个关键字(不可能比t-1少,否则就不是b树了)
// 情况3a:y 右侧的兄弟至少t个关键字,从它那借
if i+1 < len(x.children) && len(x.children[i+1].keys) >= t.t {
right := x.children[i+1]
// 将需要上升的关键字从 right 中删除
upKey := right.keys[0]
right.keys = right.keys[1:]
// 下降关键字x.keys[i]
y.keys = append(y.keys, x.keys[i])
// 上升right第一个关键字
x.keys[i] = upKey
// 如果right不是叶子节点,将孩子节点移动到 y.children 的最后
if !right.isLeaf {
y.children = append(y.children, right.children[0])
right.deleteChildAt(0)
}
return
}
// 情况3a:y的相邻兄弟x->child[i-1]包含至少t个关键字
if i-1 >= 0 && len(x.children[i-1].keys) >= t.t {
left := x.children[i-1]
// 将需要上升的关键字从 right 中删除
upKey := left.keys[len(left.keys)-1]
left.keys = left.keys[:len(left.keys)-1]
// 下降关键字x.keys[i-1]
y.insertKeyAt(x.keys[i-1], 0)
// 上升left最后一个关键字
x.keys[i-1] = upKey
// 如果left不是叶子节点,将孩子节点移动到 y.children 的开始
if !left.isLeaf {
lastIndex := len(left.children) - 1
y.insertChildAt(left.children[lastIndex], 0)
left.deleteChildAt(lastIndex)
}
return
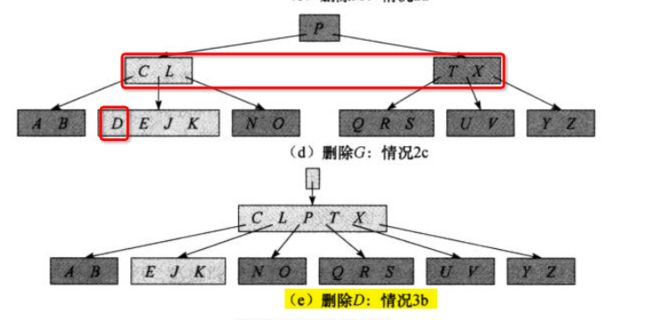
}3.b 如果子树的所有相邻兄弟节点只包含 t-1 个关键字
这时需要将子树和其中一个兄弟节点合并,合并时需要将 x 中相应的关键字移到新合并的节点中
在 (d) 中需要删除 D,当 P 成为 x 节点时,我们需要下降到 CL 所在节点,但是 CL 节点中关键字个数不满足至少 t 个,需要从相邻兄弟节点中借,但是相邻兄弟节点的关键字个数都没有大于等于 t 个的,所以,将 CL P TX 合并成一个节点。然后在新节点中递归删除关键字。
// 情况3b:相邻兄弟节点都没有足够的关键字,和其中一个合并
// 如果有右兄弟
if i+1 < len(x.children) {
// 下降关键字
y.keys = append(y.keys, x.keys[i])
x.deleteKeyAt(i)
// 合并
t.merge(y, x.children[i+1])
x.deleteChildAt(i + 1)
// 如果x是根结点并且没有关键字了,删除根节点
if x == t.root && len(x.keys) == 0 {
t.root = y
}
return
}
// 如果有左兄弟
if i-1 >= 0 {
// 下降关键字
y.insertKeyAt(x.keys[i-1], 0)
x.deleteKeyAt(i - 1)
// 合并
t.merge(y, x.children[i-1])
x.deleteChildAt(i - 1)
// 如果x是根结点并且没有关键字了,删除根节点
if x == t.root && len(x.keys) == 0 {
t.root = y
}
return
}