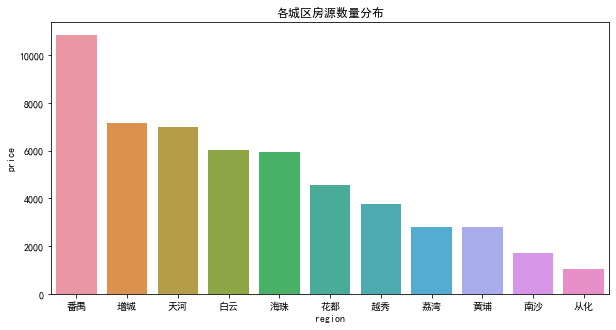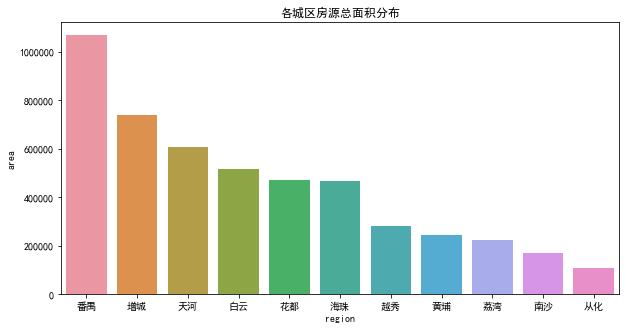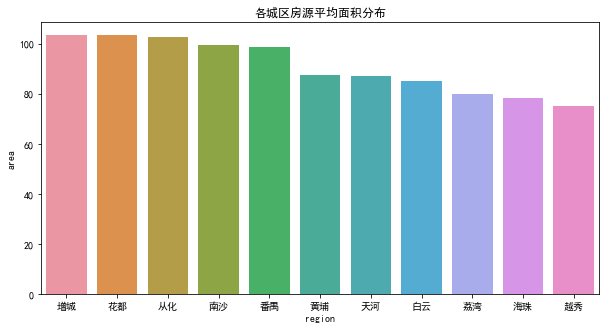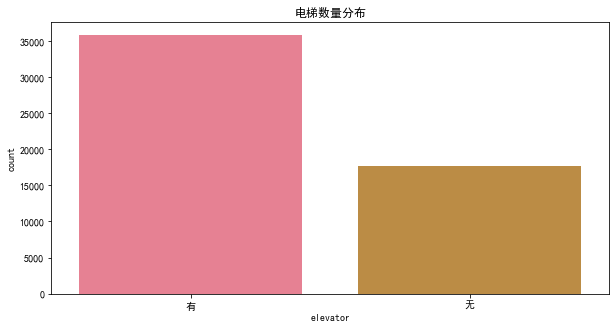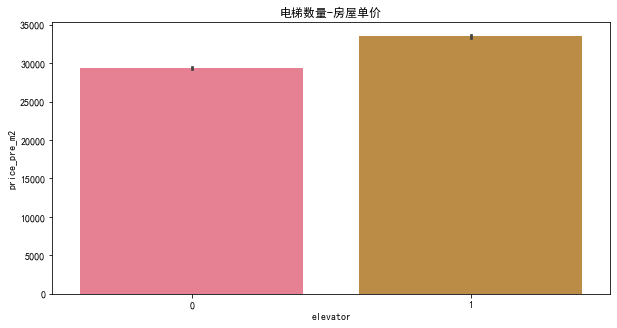分析目标
1.了解广州二手房各地区的房价情况
2.了解每个特征对房价的影响程度
3.对数据进行建模,预测房价
数据获取
从广州链家网爬取共54573条数据,数据特征如下:
price:二手房的总价格(万元)
price_per_m2:二手房的每平米价格(元)
house_type:二手房的户型
direction:二手房的朝向
area:二手房的面积
region:二手房所属的区域
built_date:二手房建成时间
elevator:是否有电梯
floor:二手房的楼层
renovation:装修情况
field:地段
xiaoqu:小区
数据导入
import pandas as pd
from pymongo import MongoClient
client = MongoClient('localhost')
db = client['lianjia']
def get_data():
data = []
for item in db['lianjiagz'].find():
data.append(item)
return data
data = get_data()
df = pd.DataFrame(data)
df.head()
首先查看数据整体情况,检查是否存在缺失值。
df.info()
RangeIndex: 54573 entries, 0 to 54572
Data columns (total 12 columns):
price 54544 non-null object
price_pre_m2 54544 non-null object
house_type 54544 non-null object
direction 54544 non-null object
area 54544 non-null object
region 54544 non-null object
built_date 54544 non-null object
elevator 53593 non-null object
floor 54544 non-null object
renovation 54221 non-null object
field 54544 non-null object
xiaoqu 54544 non-null object
dtypes: object(12)
memory usage: 5.0+ MB
数据集总共包含54573条数据,大部分特征都存在相同数量的缺失值,推测是数据爬取失败导致的空白。此外电梯存在951条缺失值,装修存在323条缺失值。
缺失值处理
删除因爬取失败导致的空白。
df.dropna(subset=['price'], inplace=True)
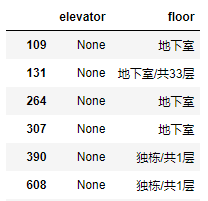
查看缺少evevator特征数据发现,存在缺失的数据,皆为地下室/低楼层/独栋,并非常规的商品房,此处选择将这些数据丢弃。
df.loc[df.elevator.isna(), ['elevator', 'floor']]
df.dropna(subset=['elevator'], inplace=True)
df.info()
Int64Index: 53593 entries, 0 to 54572
Data columns (total 12 columns):
price 53593 non-null object
price_pre_m2 53593 non-null object
house_type 53593 non-null object
direction 53593 non-null object
area 53593 non-null object
region 53593 non-null object
built_date 53593 non-null object
elevator 53593 non-null object
floor 53593 non-null object
renovation 53593 non-null object
field 53593 non-null object
xiaoqu 53593 non-null object
dtypes: object(12)
memory usage: 5.3+ MB
在处理elevator缺失值的过程中,renovation的缺失值也被舍弃了。
数据转换
去除area的单位并转换为float格式。
df.area = df.area.apply(lambda x: x.replace('平米', ''))
df.area = df.area.astype(float)
将x室x厅单独提取出来,创造两个新特征,分别为living_room和room。
import re
def get_room(x):
return re.search('(\d+)室.*?', x).group(1)
def get_living_room(x):
return re.search('\d+室(\d+)厅', x).group(1)
df['room'] = df.house_type.apply(get_room).astype(int)
df['living_room'] = df.house_type.apply(get_living_room).astype(int)
将建成年份单独提取出来。
def get_built_year(x):
if x.startswith('未知'):
return pd.NaT
else:
return re.search('(\d+)年.*?', x).group(1)
df.built_date = df.built_date.apply(get_built_year)
对direction进行处理。查看direction数据可以发现,存在一些奇怪的值,比如“东 东南 南 西南 西”这种无法理解的朝向。编写函数对direction处理后,每种方向只留下一个。
from functools import reduce
def clean_direction(x):
x = x.replace(' ', '')
direction = []
for i in x:
if i not in direction:
direction.append(i)
direction.sort()
return reduce(lambda x, y: x+y, direction)
df.direction = df.direction.apply(clean_direction)
df.direction.value_counts()
南 16989
北 9231
东南 7707
北南 4217
东 4041
东北 3275
南西 3012
北西 2092
西 2046
东西 380
东北南 206
北南西 118
东南西 116
东北南西 105
东北西 57
据数无暂 1
Name: direction, dtype: int64
将‘据数无暂’删去。
df = df.loc[df.direction != '据数无暂', :]
处理floor特征,将低、中、高楼层提取为floor_level特征,将楼层总数提取为total_floor特征。
def get_floor_level(x):
if re.search('(.*?)/.*?', x):
return re.search('(.*?)/.*?', x).group(1)
else:
return pd.NaT
def get_total_floor(x):
if re.search('.*?(\d+)层', x):
return re.search('.*?(\d+)层', x).group(1)
else:
return pd.NaT
df['floor_level'] = df.floor.apply(get_floor_level)
df['total_floor'] = df.floor.apply(get_total_floor)
转换后发现存在少量缺失值,此处选择将缺失值删去。
df.floor_level.notna().value_counts()
False 53590
True 2
Name: floor_level, dtype: int64
df = df.loc[df.floor_level.notna(),:]
数据分析
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
# 图表正常显示中文
plt.rcParams['font.sans-serif']=['SimHei']
# 正常显示符合
plt.rcParams['axes.unicode_minus']=False
描述性统计
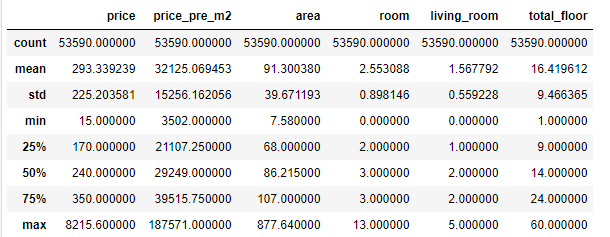
df.describe()
可以看出,二手房平均总价为293.34万元/套,中位数为240万元/套。平均每平米房价为32125元/平米,中位数为29249元/平米。平均面积为91.1平米,最大面积为877.64平米。可以看出,由于一些超大户型的影响,数据整体呈右偏趋势。
房源数量分布
df.region.value_counts().sort_values(ascending=False)
番禺 10832
增城 7153
天河 6983
白云 6044
海珠 5928
花都 4574
越秀 3753
黄埔 2792
荔湾 2792
南沙 1701
从化 1038
数据可视化
plt.figure(figsize=(10, 5))
region_count = df.groupby('region', as_index=False).count().sort_values(by='price', ascending=False)
sns.barplot(x='region', y='price', data=region_count)
plt.title('各城区房源数量分布')
从化区房源最少,不足2000套,番禺区房源最多,超过10000套,其他区房源数量在2000-8000之间。其中番禺二手房源数量占全市全区二手房数量的20.21%。
房源总面积及平均面积统计
房源总面积排序如下:
df.groupby('region').sum().area.sort_values(ascending=False)
番禺 1067891.33
增城 739562.84
天河 608179.56
白云 514934.24
花都 472354.17
海珠 465171.83
越秀 281218.75
黄埔 244319.00
荔湾 223256.17
南沙 169461.14
各城区二手房总面积分布柱形图如下:
plt.figure(figsize=(10, 5))
area_sum = df.groupby('region', as_index=False).sum().sort_values(by='area', ascending=False)
sns.barplot(x='region', y='area', data=area_sum)
plt.title('各城区房源总面积分布')
各城区二手房面积分布基本与房源数量分布一致。
接下来查看各城区二手房平均面积分布。
df.groupby('region').mean().area.sort_values(ascending=False)
增城 103.391981
花都 103.269386
从化 102.541753
南沙 99.624421
番禺 98.586718
黄埔 87.506805
天河 87.094309
白云 85.197591
荔湾 79.962812
海珠 78.470282
越秀 74.931721
可视化
plt.figure(figsize=(10, 5))
area_mean = df.groupby('region', as_index=False).mean().sort_values(by='area', ascending=False)
sns.barplot(x='region', y='area', data=area_mean)
plt.title('各城区房源平均面积分布')
总体来说,增城、花都、从化、南沙、番禺等郊区的二手房平均面积相对较大,而黄埔、天河、白云、荔湾、海珠、越秀等老城区的二手房平均面积相对较小。推测可能原因为郊区土地价格较低,较低的成本允许开发商建造更大的户型。
全市房源户型分布
以区间[0,50)、[50,100)、[100,150)、[150,200)、[200,+∞)为划分标准,将面积划分为tinysmall、small、medium、big、huge五个等级,分别对应极小户型、小户型、中等户型、大户型和巨大户型,并创造一个新特征值area_level。
df.loc[df.area < 50, 'area_level'] = 'tinysmall'
df.loc[(df.area >= 50) & (df.area < 100), 'area_level'] = 'small'
df.loc[(df.area >= 100) & (df.area < 150), 'area_level'] = 'medium'
df.loc[(df.area >= 150) & (df.area < 200), 'area_level'] = 'big'
df.loc[df.area >= 200, 'area_level'] = 'huge'
查看户型分布情况
df.groupby('area_level').count().area.sort_values(ascending=False)
small 31401
medium 13443
tinysmall 5572
big 2231
huge 943
可视化
groupped_area_level = df.groupby('area_level').area.count().reset_index().sort_values(by='area',ascending=False)
plt.figure(figsize=(10,5))
plt.bar(groupped_area_level.area_level,groupped_area_level.area)
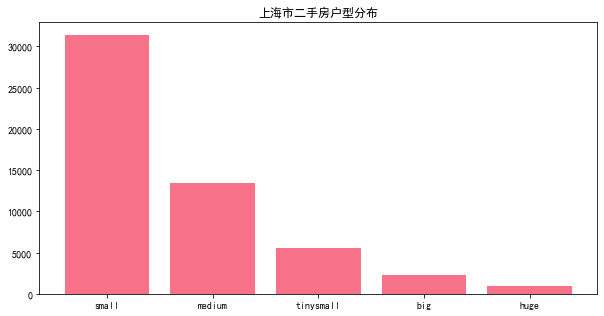
plt.title('上海市二手房户型分布')
可见,广州二手房以中小户型为主,占总数的94%以上,大户型及超大户型只占很小一部分。
各城区二手房总价及单价分布
总价分布情况
plt.figure(figsize=(10, 5))
sns.boxplot(x='region', y='price', data=df)
plt.ylim(0, 1250)
plt.grid()
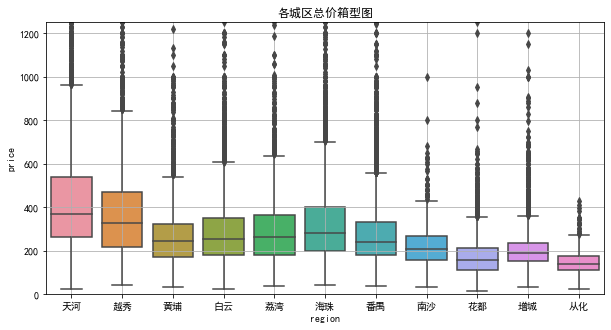
plt.title('各城区总价箱型图')
各城区平均总价排名
天河 464.750766
越秀 383.557367
海珠 329.517072
荔湾 296.762178
白云 291.132429
番禺 278.156564
黄埔 268.663933
南沙 213.583892
增城 200.978499
花都 170.217403
从化 145.550482
1.天河平均总价排第一,为464.75万元,箱型图区间为[275, 550], 中位数约为380万元,中位数比平均值小,少数价格较高的数据把整体平均值拉高了,数据呈现右偏。
2.越秀平均总价排第二,为383.56万元,箱型图区间为[210, 500],中位数约为370万元,中位数与平均值相差不大。
3.海珠、荔湾、白云二手房总价平均值和中位数都比较接近,且三者箱型图下限也比较接近,但箱型图上限有所差别。
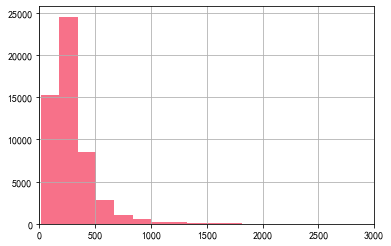
df.price.hist(bins=50)
plt.xlim(0, 3000)
约90%以上的二手房都在1000万元以下,极少数房价突破1000万元。
单价分布情况
plt.figure(figsize=(10, 5))
sns.boxplot(x='region', y='price_pre_m2', data=df)
plt.ylim(0, 125000)
plt.grid()
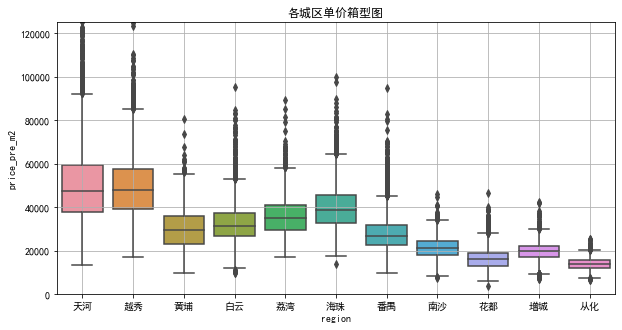
plt.title('各城区单价箱型图')
各城区平均单价排名
df.groupby('region').mean().price_pre_m2.sort_values(ascending=False)
天河 50782.225834
越秀 49305.911005
海珠 40221.435223
荔湾 35937.422994
白云 32755.814030
黄埔 29843.146848
番禺 27449.547360
南沙 21036.807760
增城 19520.788061
花都 16302.711412
从化 14006.782274
排名前三的分别是天河,越秀,海珠。
天河区均价为50782元,价格区间大约为[38000, 60000]元。
越秀区均价为49305元,价格区间大约为[40000, 59000]元。
海珠区均价为40221元,价格区间大约为[32000, 48000]元。
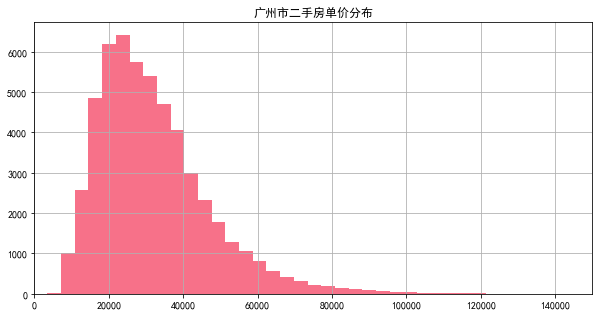
plt.figure(figsize=(10, 5))
df.price_pre_m2.hist(bins=50)
plt.xlim(0, 150000)
plt.title('广州市二手房单价分布')
二手房单价主要集中在60000元以下的区间,总体分布明显右偏,存在少数价格高的数据严重拉高了单价均值。
各小区总价及单价排名
总价排名
首先过滤掉房源较少的小区,此处取20为阈值。
df1 = df.groupby('xiaoqu').count().area.reset_index().sort_values(by='area', ascending=False)
df1 = df1[df1.area > 20]
df1 = df.loc[df.xiaoqu.isin(df.xiaoqu)]
df1.groupby('xiaoqu', as_index=False).mean().sort_values(by='price', ascending=False)[:10]
查看总价均值排名前十的小区。
df1.groupby('xiaoqu').mean().price.sort_values(ascending=False)[:10]
嘉裕公馆 1684.22
粤海丽江花园 1671.81
凯旋新世界枫丹丽舍 1563.47
中海璟晖华庭 1212.66
隽峰苑 1177.27
星汇云锦 1104.36
南国花园 951.25
东风广场 927.52
朱美拉公寓 909.83
西关海 895.60
plt.figure(figsize=(20, 5))
xiaoqu_price = df1.groupby('xiaoqu', as_index=False).mean().sort_values(by='price', ascending=False)[:10]
sns.barplot(x='xiaoqu', y='price', data=xiaoqu_price)
plt.title('全市总价排名前十的小区')
总价排名前10的小区均超过了895万元,排前两名的嘉裕公馆和粤海丽江花园相差不大,总价都在1600万元以上。
单价排名
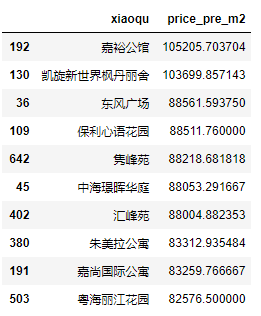
xiaoqu_price_pre_m2 = df1.groupby('xiaoqu', as_index=False).mean().sort_values(by='price_pre_m2', ascending=False)[:10]
xiaoqu_price_pre_m2[['xiaoqu', 'price_pre_m2']]
plt.figure(figsize=(20, 5))
sns.barplot(x='xiaoqu', y='price_pre_m2', data=xiaoqu_price_pre_m2)
plt.title('全市单价排名前十的小区')
排名前十的小区单价均超过了8万元/平米,其中嘉裕公馆和凯旋新世界枫丹丽舍遥遥领先,其余小区之间的差距并不大。
房价与楼层的关系
plt.figure(figsize=(10, 5))
floor_level_price_per_m2 = df.groupby('floor_level', as_index=False).mean().sort_values(by='price_pre_m2', ascending=False)
sns.barplot(x='floor_level', y='price_pre_m2', data=floor_level_price_per_m2)
plt.title('不同楼层等级与房价的关系')
可以明显看出,不同楼层等级之间,房价单价并没有明显的差距,都在30000元以上。不同楼层对房价没有太大的影响。
plt.figure(figsize=(10, 5))
floor_price = df.groupby('total_floor', as_index=False).mean().sort_values(by='price_pre_m2', ascending=False)
sns.lineplot(x='total_floor', y='price_pre_m2', data=floor_price)
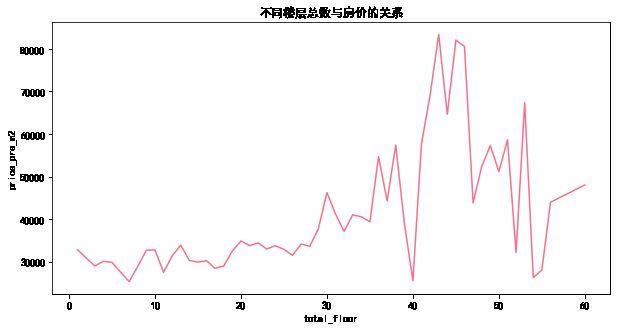
plt.title('不同楼层总数与房价的关系')
由上图分析可知,随着楼层数目的增加,房价也随之升高。在40层之前,房价随楼层数增加而增加的趋势比较线性,但是在这之后房价随楼层数增加而增加的趋势波动很大,可能的原因是楼层数超过40的住宅数量较小,超过40层的数据量比较小,容易产生误差。
房价与朝向的关系
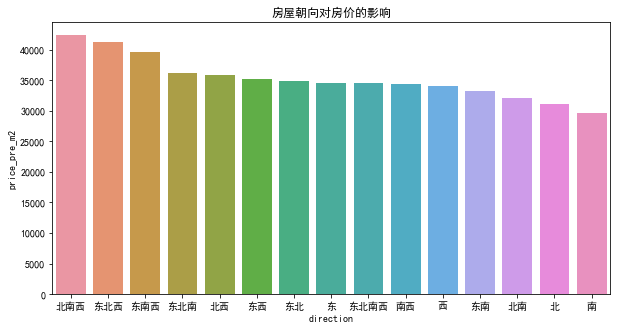
plt.figure(figsize=(20, 15))
direction_price = df.groupby('direction', as_index=False).mean().sort_values(by='price_pre_m2', ascending=False)
sns.barplot(x='direction', y='price_pre_m2', data=direction_price)
可以看出,朝向对房价有一定的影响,但由于朝向数值比较复杂,并不是单一的东南西北,无法具体推测房价到底受什么朝向影响。
房价与户型的关系
上文中已将户型拆分为房间数(room)和客厅数(living_room),下文将分别探索这两个特征与房价的关系。
room
df.room.value_counts()
3 22674
2 19293
1 5897
4 4577
5 930
6 152
7 39
8 10
0 5
9 4
12 2
13 1
10 1
房间数以1-4个为主,占全部数据的90%以上。此外,存在一些数据量较少的房间数,这里选择将数量为100以下的房间数都删去。
df2 = df.groupby('room').count().area.reset_index().sort_values(by='area', ascending=False)
df2 = df2[df2.area > 20]
df2 = df.loc[df.room.isin(df2.room)]
5 35080.61
6 33549.43
1 33417.01
4 33253.89
2 32815.55
3 30831.33
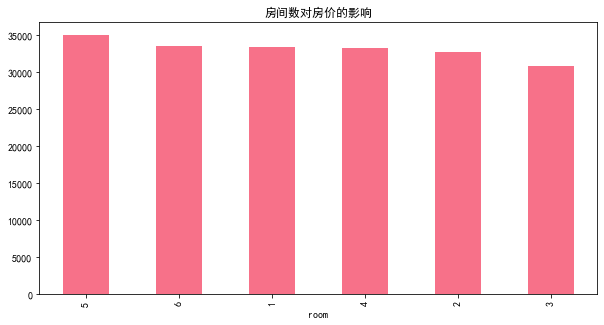
plt.figure(figsize=(10, 5))
df2.groupby('room').mean().sort_values(by='price_pre_m2', ascending=False)[:10].price_pre_m2.plot(kind='bar')
plt.title('房间数对房价的影响')
房间数量对房价影响程度较低,侧面反映了在选购二手房时,买房对房间数量没有特别的偏好。
living_room
df2.living_room.value_counts()
2 31221
1 20587
0 1441
3 253
4 18
5 3
客厅数量主要为0-3个,过滤掉不足20条数据的living_room。
df3 = df2.groupby('living_room').count().area.reset_index().sort_values(by='area', ascending=False)
df3 = df3[df3.area > 20]
df3 = df.loc[df.living_room.isin(df3.living_room)]
df3.groupby('living_room').mean().price_pre_m2.sort_values(ascending=False)
1 33904.73
3 33371.71
0 33300.13
2 30885.00
plt.figure(figsize=(10, 5))
df3.groupby('living_room').mean().sort_values(by='price_pre_m2', ascending=False)[:10].price_pre_m2.plot(kind='bar')
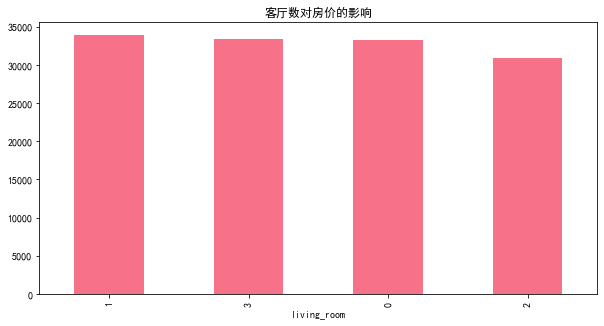
plt.title('客厅数对房价的影响')
平均单价最高的是1客厅的小户型,3客厅及0客厅紧随其后,三者之间单价相差不大。平均单价最低的是2客厅的户型。可能原因是,随着房价的上涨,小户型由于总价较低的原因,更受市场的青睐。
房屋与建成年代的关系
plt.figure(figsize=(10, 5))
df.groupby('built_date').count().area.plot()
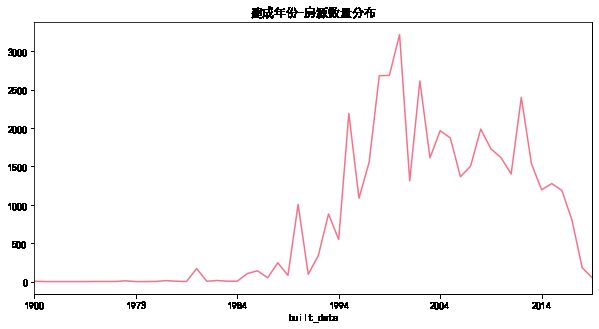
plt.title('建成年份-房源数量分布')
图形呈双峰状态,分别在1999年和2013年出现了两个房屋建筑的高峰。
plt.figure(figsize=(10, 5))
df.groupby('built_date').mean().price.plot()
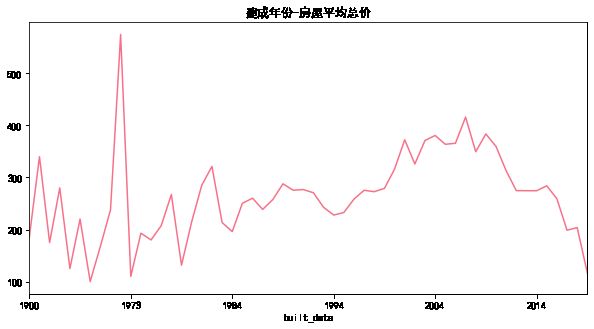
plt.title('建成年份-房屋平均总价')
1973年以前建成的房屋总价最高,可能原因是早年间房屋都在城市的核心区域即市中心建成。1973年后房价逐渐上升,在2009年达到高峰,之后开始下滑。可能原因是,1973年后房屋大多在郊区建成,由于较低的土地成本,郊区的房屋面积更大,总价便水涨船高。2009年后房屋总价逐渐下滑的原因可能是,09年后房屋大多在增城、从化等地建成,由于其相对其他城区较低的房价,房屋总价也在逐渐下降。
plt.figure(figsize=(10, 5))
df.groupby('built_date').mean().price_pre_m2.plot()
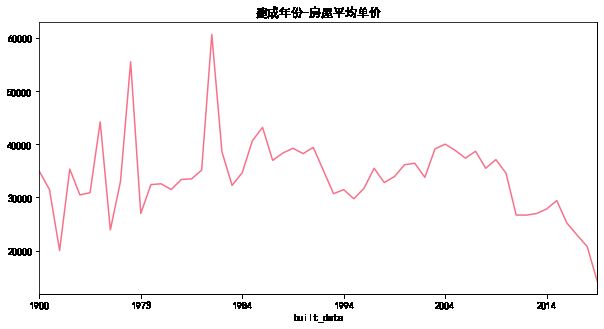
plt.title('建成年份-房屋平均单价')
由建成年份-房屋单价图可以看出,其趋势符合上文的推测,即早年间的房屋建在市中心故单价较高。其后房屋大多建在郊区,单价逐渐下降。
电梯与房价的关系
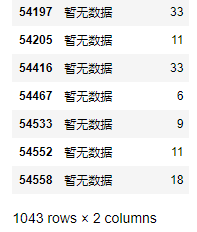
df.loc[df.elevator == '暂无数据', ['elevator', 'total_floor']]
可以看出,elevator特征存在1043行缺失值,此处考虑基于楼层总数填补缺失值。一般默认大于7层楼的住宅拥有电梯,小于7层楼的住宅没有电梯。此处将暂无数据进行替换。
df.loc[(df.elevator == '暂无数据') & (df.total_floor > 7), 'elevator'] = 1
df.loc[(df.elevator == '暂无数据') & (df.total_floor <= 7), 'elevator'] = 0
查看一下电梯数量分布。
plt.figure(figsize=(10, 5))
sns.countplot(x='elevator', data=df)
plt.title('电梯数量分布')
可以看出,超过60%的房屋都拥有电梯,无电梯的房屋数量只占有电梯的一半。
plt.figure(figsize=(10, 5))
sns.barplot(x='elevator', y='price_pre_m2', data=df)
plt.title('电梯数量-房屋单价')
由图看出,有电梯的房屋单价比没有电梯的房屋单价要高,这也符合我们的常识。
特征工程
首先对categorical类型的特征进行one-hot处理。
def get_dummies(column, prefix):
global df
dummies = pd.get_dummies(df[column], prefix=prefix)
df = pd.concat([df, dummies], axis=1)
needed_get_dummies = ['renovation', 'direction', 'region', 'floor_level', 'field', 'xiaoqu', 'area_level']
for needed in needed_get_dummies:
get_dummies(needed, prefix=needed)
df.drop(needed, axis=1, inplace=True)
其次对连续型变量进行标准化处理,此处用到的是MinMaxScaler
from sklearn.preprocessing import MinMaxScaler
def scaler(column):
global df
scaler = MinMaxScaler()
df[column] = scaler.fit_transform(df[column].values.reshape(-1, 1))
needed_scale = ['area', 'room', 'living_room', 'total_floor']
for needed in needed_scale:
scaler(needed)
将房屋单价作为模型的target,并归一化。
y = df.pop('price_pre_m2')
y = MinMaxScaler().fit_transform(y.values.reshape(-1, 1))
df.drop(['price', 'house_type', 'built_date', 'floor'], axis=1, inplace=True)
特征选择
df.shape
(53585, 5400)
由于特征数量较多,需要用特征选择,选出有用变量,删去无用变量。可以使用随机森林、gbdt等模型进行特征选择。对于回归问题,通常采用的是方差或者最小二乘拟合。当训练决策树的时候,可以计算出每个特征减少了多少树的不纯度。对于一个决策树森林来说,可以算出每个特征平均减少了多少不纯度,并把它平均减少的不纯度作为特征选择的值。
此处采用的是gbdt模型进行特征选择,保留feature_importance累计前99%的特征。
from sklearn.ensemble import GradientBoostingRegressor
X = df.values
names = df.columns
def get_importance(X, y, names):
gbdt = GradientBoostingRegressor(n_estimators=500)
gbdt.fit(X, y)
feature_importance = pd.Series(dict(zip(names, map(lambda x: round(x, 4), gbdt.feature_importances_))))
return feature_importance
feature_importance = get_importance(X, y, names)
feature_importance = feature_importance.sort_values(ascending=False)
sum = 0
features = []
for k, v in enumerate(feature_importance):
if sum > 0.99:
break
else:
sum += v
features.append(feature_importance.index[k])
print(len(features))
233
通过gbdt模型进行特征选择,保留了233个特征。
X = df[features]
建模
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=0)
将数据分为训练集和测试集,由于数据量有5万多条,此处选择测试集的test_size为0.1。用更多的数据进行训练。
使用keras建立神经网络模型。
import tensorflow as tf
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input, Dense, BatchNormalization, Activation
from tensorflow.keras.optimizers import Adam, RMSprop, SGD
from tensorflow.keras.regularizers import l2
from tensorflow.keras.callbacks import ReduceLROnPlateau, ModelCheckpoint, LearningRateScheduler
def create_model():
input = Input(shape=(X.shape[1],))
x = Dense(128, kernel_regularizer=l2(0.1))(input)
x = Activation('relu')(x)
x = BatchNormalization(axis=-1)(x)
x = Dense(256, kernel_regularizer=l2(0.1))(x)
x = Activation('relu')(x)
x = BatchNormalization(axis=-1)(x)
x = Dense(256, kernel_regularizer=l2(0.1))(x)
x = Activation('relu')(x)
x = BatchNormalization(axis=-1)(x)
x = Dense(128, kernel_regularizer=l2(0.1))(x)
x = Activation('relu')(x)
x = BatchNormalization(axis=-1)(x)
x = Dense(64, kernel_regularizer=l2(0.1))(x)
x = Activation('relu')(x)
x = BatchNormalization(axis=-1)(x)
x = Dense(64, kernel_regularizer=l2(0.1))(x)
x = Activation('relu')(x)
x = BatchNormalization(axis=-1)(x)
x = Dense(1)(x)
model = Model(inputs=input, outputs=x)
return model
model = create_model()
model.compile(optimizer=SGD(1e-2), loss='mean_squared_error', metrics=['mse', 'mae'])
建立了一个7层神经网络模型,其每层神经元数量分别是128,256,256,128,64,64,1。除了最后一层输出层外,每一层都加入了一个l2正则项,正则化系数为0.1,目的是防止过拟合。激活函数使用的是relu激活函数,在激活函数后加入了一个batch normalization层,可以加快收敛速度。模型的优化器使用sgd即随机梯度下降,初始学习率定为1e-2,loss为均方差。
lrReduce = ReduceLROnPlateau(monitor='val_loss', factor=0.5, patience=10)
filepath="/content/drive/My Drive/tmp/sgd4_weights-improvement-{epoch:03d}-{val_loss:.4f}.hdf5"
checkpoint= ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
def scheduler(epoch):
lr_base = 1e-2
decay = 0.3
lr = lr_base * (0.95 ** epoch)
return lr
lrScheduler = LearningRateScheduler(scheduler)
为模型加入了三个回调对象。分别是LearningRateScheduler即衰减学习率。ReduceLROnPlateau用于监视学习率,当loss不再下降时,将学习率减半。ModelCheckpoint,作用分别是保存最好的模型。
history = model.fit(X_train, y_train, batch_size=128, epochs=200, validation_data=(X_test, y_test), callbacks=[lrReduce, checkpoint])
开始训练,训练200个epochs,batch_size选128。
Epoch 00199: val_loss improved from 0.30553 to 0.30284, saving model to /content/drive/My Drive/tmp/sgd4_weights-improvement-199-0.3028.hdf5
训练完成后可见,最小的验证集误差为0.30284。
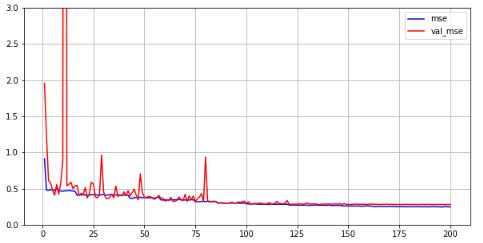
mse = history.history['mean_squared_error']
val_mse = history.history['val_mean_squared_error']
plt.figure(figsize=(10, 5))
plt.plot(range(1, 201), mse, c='b', label='mse')
plt.plot(range(1, 201), val_mse, c='r', label='val_mse')
plt.grid()
plt.ylim(0, 3)
plt.legend()
绘制训练集-测试集误差曲线,可以看出测试集误差整体随训练集误差下降。在100个epoch前测试集误差会有较大的波动,之后逐渐趋于平稳,最终收敛不再下降。
from tensorflow.keras.models import load_model
model1 = load_model('/content/drive/My Drive/tmp/sgd4_weights-improvement-199-0.3028.hdf5')
print(r2_score(y_test, model1.predict(X_test)))
0.8750705820051174
模型在测试集上的r2系数为0.875,预测准确度还算可以。
总结
1.二手房单价受地理因素影响较大,不同城区之间房屋单价差异较大,最高的天河区平均单价为50782元/平米,最低的从化区平均单价为14006元/平米同一城区不同小区的房屋单价也有较大的差异。最贵的小区,房屋单价高达10万元,远远超过城区的均价。
2.二手房的数量和总面积可以反映市场的大小。番禺区二手房源数量10832套,占全市所有房源的20.21%,其二手房总面积为1067891.33平米为全市最高。不管从数量还是面积来看,番禺的二手房市场都是全区最大的,主要原因为其平均单价为27000元/平米,仅为天河区的一半。
3.楼层、户型、朝向、电梯等要素对二手房的单价也有影响,但影响并不显著。
4.建成年份可以反映房屋的建造时间,进一步可以推测房屋大概的建造地点,从而推测房价。越早建成的房屋越倾向于建于市中心,反之则倾向于建在郊区。
5.模型对测试集的r2系数为0.875,不算特别好。后续可以通过爬取更多的特征、创建更多的特征、优化模型结构、调参等方式来优化模型的表现。