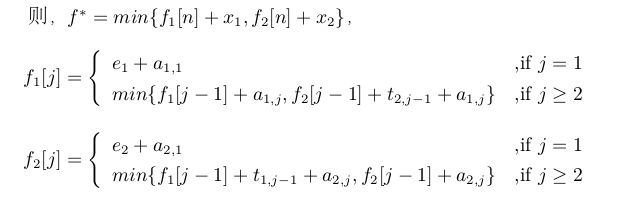lienhua34
2014-10-06
1 问题描述
某个汽车工厂共有两条装配线,每条有 n 个装配站。装配线 i 的第 j个装配站表示为 Si,j ,在该站的装配时间为 ai,j 。一个汽车底盘进入工厂,然后进入装配线 i(i 为 1 或 2),花费时间为 ei 。在通过一条线的第 j 个装配站后,这个底盘来到任一条装配线的第(j+1)个装配站。如果它留在相同的装配线,则没有移动开销。但是,如果它移动到另一条线上,则花费时间为 ti,j 。在离开一条装配线的第 n 个装配站后,完成的汽车底盘花费时间为 xi 离开工厂。待求解的问题是,确定应该在装配线 1 内选择哪些站,在装配线 2 内选择哪些站,才能使汽车通过工厂的总时间最短。
2 算法解析
下面通过动态规划思想来对该装配线调度问题分步骤进行解析。
2.1 步骤 1:描述最优解结构的特征
观察一条通过装配站 S1,j 的最快路线,发现它必定是经过装配线 1 或2 上的装配站(j-1)。因此,通过装配站 S1,j 的最快路线只能是以下二者之一:
• 通过装配站 S1,j−1 的最快路线,然后直接通过装配站 S1,j 。
• 通过装配站 S2,j−1 的最快路线,从装配线 2 转移到装配线 1,然后通过装配站 S1,j 。
故寻找通过任一条装配线上的装配站 j 的最快路线,我们可以规划为先寻找通过两条装配线上的装配站 j-1 的最快路线。
2.2 步骤 2: 利用问题的最解递归定义一个最优解的值
记 fi [j] 表示一个汽车底盘从起点到装配站 Si,j 的最快可能时间;f ∗ 表示底盘通过工厂的所有装配站的最快时间。
2.3 步骤 3:计算最快时间
递归算法的执行时间是关于 n 的指数形式,所以我们采用从低向上的实现方法计算最快时间。记 li [j] 表示进入装配站 Si,j 的前一个装配站来自哪条装配线;l∗ 表示从哪一条装配线离开工厂。
FATEST-WAY(a, t, e, x, n) f1 [1] ← e1 + a1,1 f2 [1] ← e2 + a2,1 for j ← 2 to n if f1 [j − 1] + a1,j ≤ f2 [j − 1] + t2,j−1 + a1,j then f1 [j] ← f1 [j − 1] + a1,j l1 [j] ← 1 else f1 [j] ← f2 [j − 1] + t2,j−1 + a1,j l1 [j] ← 2 endif if f2[j − 1] + a2,j ≤ f1 [j − 1] + t1,j−1 + a2,j then f2 [j] ← f2 [j − 1] + a2,j l2 [j] ← 2 else f2[j] ← f1 [j − 1] + t1,j−1 + a2,j l2 [j] ← 1 endif endfor if f1 [n] + x1 ≤ f2 [n] + x2 then f∗ ← f1 [n] + x1 l∗ ← 1 else f∗ ← f2 [n] + x2 l∗ ← 2 endif end
2.4 步骤 4:构造通过工厂的最快路线
根据步骤 3 获得的 li [j] 和 l∗ 来打印出装配线调度耗时最小的路线。
PRINT-STATIONS(l, l∗ , n) i ← l∗ print ’line:’ i ’, station:’ n for j ← n downto 2 i ← li [j] print ’line:’ i ’, station:’ j-1 endfor end
3 C 语言实现验证
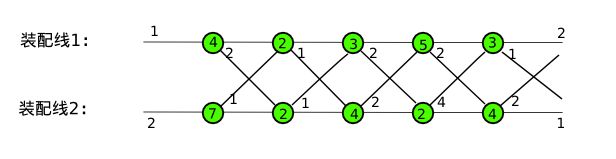
现在假设有两条各自有 5 个装配站的装配线,其装配线各站点调度耗时如下图所示,
图 1: 装配线示例图
其中,装配线左边是入口,右边是出口,入口和出口上的数字分别表示进入装配线和离开装配线的耗时。绿色圆圈表示装配站,圆圈中的数字表示在该装配站上的装配时间。各个装配线之间连线上的数字表示从一个条装配线的转移到另一条装配线消耗的时间。
使用 C 语言的验证代码如下所示,
#include#include void PrintPath(int *, int , int); void FastestWay(int *, int *, int [], int [], int); int main(void) { int enterTimes[2] = {1, 2}; int exitTimes[2] = {2, 1}; int assemblyTimes[2][5] = { {4, 2, 3, 5, 3}, {7, 2, 4, 2, 4}}; int transferTimes[2][5] = { {2, 1, 2, 2, 1}, {1, 1, 2, 4, 2}}; FastestWay(&assemblyTimes[0][0], &transferTimes[0][0], enterTimes, exitTimes, 5); exit(0); } void FastestWay(int *assemblyTimes, int *transferTimes, int enterTimes[2], int exitTimes[2], int n) { int fastestTime = 0; int exitLine; int j; int *fastest, *lineTag; int temp1, temp2; fastest = malloc(sizeof(int) * 2 * n); lineTag = malloc(sizeof(int) * 2 * n); *(fastest) = enterTimes[0] + *assemblyTimes; *(fastest + n) = enterTimes[1] + *(assemblyTimes + n); for (j = 1; j < n; j++) { temp1 = *(fastest + (j-1)); temp2 = *(fastest + (n + j - 1)) + *(transferTimes + (n + j - 1)); if (temp1 <= temp2) { *(fastest + j) = temp1 + *(assemblyTimes + j); *(lineTag + j) = 1; } else { *(fastest + j) = temp2 + *(assemblyTimes + j); *(lineTag + j) = 2; } temp1 = *(fastest + (n + j - 1)); temp2 = *(fastest + (j - 1)) + *(transferTimes + (j - 1)); if (temp1 <= temp2) { *(fastest + (n + j)) = temp1 + *(assemblyTimes + (n + j)); *(lineTag + (n + j)) = 2; } else { *(fastest + (n + j)) = temp2 + *(assemblyTimes + (n + j)); *(lineTag + (n + j)) = 1; } } temp1 = *(fastest + (n - 1)) + exitTimes[0]; temp2 = *(fastest + (n + n - 1)) + exitTimes[1]; if (temp1 <= temp2) { fastestTime = temp1; exitLine = 1; } else { fastestTime = temp2; exitLine = 2; } printf("The cost of the fastest path: %d\n", fastestTime); PrintPath(lineTag, exitLine, n); } void PrintStation(int line, int station) { printf("line: %d, station: %d\n", line, station); } void PrintPath(int *lineTag, int exitLine, int n) { int i = exitLine; int j; PrintStation(exitLine, 5); for (j = 5; j >= 2; j--) { i = *(lineTag + (n * (i - 1) + j - 1)); PrintStation(i, j-1); } }
编译该程序,生成并执行文件 AssemblyLineSchedule,
lienhua34:algorithm$ gcc -o AssemblyLineSchedule AssemblyLineSchedule.c lienhua34:algorithm$ ./AssemblyLineSchedule The cost of the fastest path: 19 line: 2, station: 5 line: 2, station: 4 line: 2, station: 3 line: 1, station: 2 line: 1, station: 1
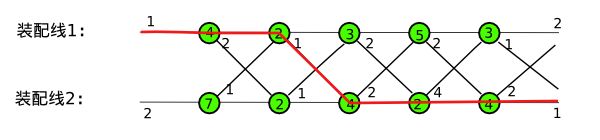
于是,最短路径总共耗时 19,其路径如下图中的红色线条,
图 2: 含有最快路径的装配线示例图
(done)