leetcode第一周题解整理

题目	难易程度	题号
twoSum	easy	1
isValid	easy	20
removeElement	easy	27
plusOne	easy	66
singleNumber	easy	136
titleToNumber	easy	171
rob	easy	198
threeSum	middle	15
permute	middle	46
canJump	middle	55
hasCycle	middle	141
detectCycle	middle	142

代码传送门: github_offer_plus

twoSum（两数之和）

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，你不能重复利用这个数组中同样的元素

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

解法一：暴力方法

利用两个下标i,j对数组进行遍历，判断i,j所指向的两个数的和是否为 target
该方法大家都能想到，由于当i指向某个下标的时候,j需要去遍历数组中i后面的元素，所以时间复杂度是O(n^2)，空间复杂度是O(1)

    public static int[] twoSum(int[] nums, int target) {
        for(int i = 0; i < nums.length - 1; i++){
                for(int j = i+1; j < nums.length;j++){
                    if(nums[i] + nums[j] == target)return new int[]{i,j};
                }
        }
        throw new IllegalArgumentException("no sum");
    }

解法二：借助哈希表，以空间换时间

题目要求返回的结果是两个数的下标，如果利用哈希表设置从数值到下标的映射，可以快速得到下标，而利用哈希表查找某个数的时间可以近似为 O(1)，遍历数组的时间复杂度是O(n)，所以最后算法的时间复杂度是 O(n)，空间复杂度是 O(n)

首先遍历数组完成数值到下标的映射；
再次遍历数组，判断哈希表中是否存在目标值减去当前遍历元素的值，若存在，return，若不存在继续遍历

    public static int[] twoSum1(int [] nums,int target){
        Map<Integer,Integer> tmp = new HashMap<>();
        for(int i = 0; i < nums.length;i++){
            tmp.put(nums[i],i);
        }
        for(int i = 0;i < nums.length;i++){
            if(tmp.containsKey(target - nums[i]) && tmp.get(target - nums[i]) != i){
                return new int[]{i,tmp.get(target - nums[i])};
            }
        }
        throw new IllegalArgumentException("");
    }

注：哈希表中存储的是该数值对应数组中的最后一个下标，所以如果两个下标不一样的话，可以直接返回，如果一样的话，说明数组中只有一个该元素，应该继续遍历

解法二的优化：

    public static int[] twoSum2(int [] nums,int target){
        Map<Integer,Integer> tmp = new HashMap<>();
        for(int i = 0; i < nums.length;i++){
            int component = target - nums[i];
            if(tmp.containsKey(component))return new int[]{tmp.get(component),i};
            tmp.put(nums[i],i);
        }
        throw new IllegalArgumentException("");
    }

isValid（有效的括号）

给定一个只包括 ‘(’，’)’，’{’，’}’，’[’，’]’ 的字符串，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。

示例 1:

输入: "()"
输出: true
示例 2:

输入: "()[]{}"
输出: true
示例 3:

输入: "(]"
输出: false
示例 4:

输入: "([)]"
输出: false
示例 5:

输入: "{[]}"
输出: true

解法一：栈

括号匹配问题是栈的典型应用，根据栈先进后出的原则，可以在进行匹配的时候匹配栈顶元素，也就是最新进展的元素，遇到左括号进栈，遇到右括号出栈，如果出栈的左括号和右括号不匹配则返回false，若匹配，遍历下一个元素，遍历结束判断栈是否为空，如果栈不空，说明有还未匹配的左括号，返回false.

对字符串只执行了一次遍历，时间复杂度为O(n)，空间复杂度为O(n)

    public static boolean isValid(String s) {
        Stack<Character> tmp = new Stack<Character>();
        for(int i = 0; i < s.length();i++){

            if(s.charAt(i) == '{' || s.charAt(i) == '[' || s.charAt(i) == '('){
                tmp.push(s.charAt(i));
            }else if(s.charAt(i) == '}' || s.charAt(i) == ']' || s.charAt(i) == ')'){

                /**
                 * pop出栈的时候一定要判断栈是否为空
                 * */
                if(tmp.empty())return false;
                char t = tmp.pop();
                if(!(t == '{' && s.charAt(i) == '}' || t == '[' && s.charAt(i) == ']' || t == '(' && s.charAt(i) == ')'))
                    return false;
            }
        }

        return tmp.empty();

    }

注：执行出栈的时候一定要判断栈是否为空

removeElement（移除元素）

给定一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，返回移除后数组的新长度。

不要使用额外的数组空间，你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

示例 1:

给定 nums = [3,2,2,3], val = 3,

函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。

你不需要考虑数组中超出新长度后面的元素。
示例 2:

给定 nums = [0,1,2,2,3,0,4,2], val = 2,

函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。

注意这五个元素可为任意顺序。

你不需要考虑数组中超出新长度后面的元素。

解法一：双指针遍历,头尾指针

下标索引i从头开始遍历，下标索引tail从数组尾部开始遍历，若下标i指向的元素不为目标元素，下标i向后传递，否则，将tail指向的元素复制到i指向的位置，tail向前移动一位，直到i大于等于tail，若此时两个下标相等并且指向的元素为目标元素，输出的长度就是tail，否则输出tail+1
时间复杂度为O(n),空间复杂度为O(1)

    public static int removeElement(int[] nums, int val) {
        int len = nums.length;
        int tail = len - 1;
        int i = 0;
        while (i < tail){
            if(nums[i] != val){
                i++;
            }else{
                nums[i] = nums[tail];
                tail --;
            }
        }
        if(i == tail &&nums[i] == val){
            return tail;
        }else return tail + 1;
    }

解法二：双指针，快慢指针

同样使用双指针，只是这个方法的两个指针都从头开始，指针i指向原数组该被更新的位置，索引i前面的元素都不为目标元素，指针j遍历数组，如果j指向的元素为目标元素，j向后传递，否则，将j指向的元素赋值给i指向的位置，i向后传递
该种方法的时空复杂度和解法一相同，和解法一相比的有点就是可以保证，元素都是按照原来的顺序进行排列的,缺点就是需要对和目标元素不相等的元素执行赋值操作，但是这个缺点是相对的，如果相同元素比较多，用该种方法比较好，如果不同的元素比较多，用解法一比较好

public int removeElement(int[] nums, int val) {
    int i = 0;
    for (int j = 0; j < nums.length; j++) {
        if (nums[j] != val) {
            nums[i] = nums[j];
            i++;
        }
    }
    return i;
}

plusOne（加一）

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位， 数组中每个元素只存储单个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

示例 1:

输入: [1,2,3]
输出: [1,2,4]
解释: 输入数组表示数字 123。
示例 2:

输入: [4,3,2,1]
输出: [4,3,2,2]
解释: 输入数组表示数字 4321。

解法一：从后向前遍历

从数组最后一个位置向前遍历，先执行最后一个元素加1，如果执行之后元素大于9，则将该位置元素赋值0，遍历指针向前移动，依次加1，直到指针指向的元素小于10，如果最后指针指向第一个元素，并且最后结果大于9，将第一个元素赋值0，在索引0位置插入1

    public static int[] plusOne(int[] digits) {
        int len = digits.length;
        digits[len - 1] += 1;
        int i = len - 1;
        while (digits[i] > 9 && i > 0){
            digits[i] = 0;
            i--;
            digits[i] += 1;
        }
        ArrayList<Integer> res1 = new ArrayList<Integer>();
        if(i == 0 && digits[i] > 9){
            digits[i] = 0;
            int [] res = new int[digits.length + 1];
            res[0] = 1;
            return res;
        }
        return digits;

    }

singleNumber（只出现一次的数字）

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,1]
输出: 1
示例 2:

输入: [4,1,2,1,2]
输出: 4

解法一：位运算

借助位运算中的异或运算，这也是我第一次接触位运算，还没有太多的感悟，
参加运算的两个数，按二进制位进行“异或”运算,参加运算的两个数，如果两个相应位为“异”（值不同），则该位结果为1，否则为0。
但是这里比较的是二进制的比较，而不是十进制，比如6 ^ 6 = 110 ^ 110 = 0
4 ^ 6 = 100 ^ 110 = 010 = 2
2 ^ 4 = 010 ^ 100 = 110 = 6
所以如果数组中出现两次的数字进行异或运算都是0，剩下的就是只出现一次的数字

    public static int singleNumber(int[] nums) {
        int v = 0 ;
        for(int x:nums){
            v ^= x;
        }
        return v;
    }

• leetcode官方题解给了好几种方法，之后再补充

titleToNumber（Excel表列序号）

给定一个Excel表格中的列名称，返回其相应的列序号。
例如，

A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28 
...

示例 1:

输入: "A"
输出: 1
示例 2:

输入: "AB"
输出: 28
示例 3:

输入: "ZY"
输出: 701

解法一：数学解法

    public int titleToNumber(String s) {
        int len = s.length();
        int res = 0;
        for(int i = 0;i < len;i++){
            res += Math.pow(26,i) + (s.charAt(i) - 'A') * Math.pow(26,len - i - 1);
        }
        return res;
    }

解法二：26进制

A-Z一共26个字母，每26个字母向前进一位，所以相当于26进制，即将26进制的数字转成为十进制

比如321（八进制） = 3
$$321(八进制)=3\ast 8^2+2\ast 8^1+1\ast 8^0$$

那么(26进制不好表示，用列表将几个数分开吧)
$$[23,1,10](26进制)=23\ast 26^2+1\ast 26^1+10\ast 26^0$$
所以 A -> 1,Z->26
$$AZB=1\ast 26^2+26\ast 26^1+2\ast 26^0$$

若 A -> 0,Z->25
$$AZB=0\ast 26^2+25\ast 26^1+1\ast 26^0$$

    public int titleToNumber(String s) {
        int ans = 0;
        for(int i=0;i<s.length();i++) {
            int num = s.charAt(i) - 'A' + 1;
            ans = ans * 26 + num;
        }
        return ans;
    }

rob（打家劫舍）

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额

示例 1:

输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:

输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12 。

解法一：动态规划

自己太笨了，没有想出来，直接看官方题解吧
设f(k)表示一共k个房屋的最高金额
对于n=1的情况，f(1) = nums[0]
对于n=2的情况，f(2) = max(f(1),nums[1])
对于n = 3的情况，要么选择抢劫，f(3) = f(1) + nums[2]，要么放弃，f(3) = f(2)
所以
$$f(k)=max(f(k-2)+nums[k],f(k-1))$$

    public static int rob1(int[] nums) {
        int res = 0;
        int preRes = 0;
        for(int x:nums){
            int tmp = res;
            res = Math.max(preRes + x,res);
            preRes = tmp;
        }
        return res;
    }

threeNumber（三数之和）

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4]，

满足要求的三元组集合为：
[
  [-1, 0, 1],
  [-1, -1, 2]
]

解法一：三指针遍历

首先对数组进行从小到大的排序
利用三个指针i \ L \ R进行遍历，外层循环i指针从前向后遍历，内层循环L从i+1开始向后遍历，R从len-1开始遍历，固定i，指针L 、 R向中间遍历，若nums[i]+nums[L]+nums[R] = 0，L R指针同时向中间移动，若L >= R跳出内层循环，若nums[i]+nums[L]+nums[R] > 0,R左移，若nums[i]+nums[L]+nums[R] < 0,L右移

附上清晰的题解连接

    public static List<List<Integer>> threeSum2(int[] nums){
        if(nums.length < 3)return new ArrayList<>();
        Arrays.sort(nums);
        int L;
        int R;
        Set<List<Integer>> result = new HashSet<>();
        for(int i = 0;i < nums.length - 2;i++){
            L = i + 1;
            R = nums.length - 1;
            if(!(i > 0 && nums[i] == nums[i - 1])){
                while (L < R){
                    if(nums[i] + nums[L] + nums[R] == 0){
                        ArrayList<Integer> r = new ArrayList<>();
                        r.add(nums[i]);
                        r.add(nums[L]);
                        r.add(nums[R]);
                        result.add(r);
                        L++;
                        R--;
                    }else if(nums[i] + nums[L] + nums[R] > 0){
                        R--;
                    }else if(nums[i] + nums[L] + nums[R] < 0){
                        L++;
                    }
                }
            }


        }
        return new ArrayList<>(result);

    }

思路二：twoSum的启发

不能叫解法了，因为最后两个测试案例由于时间超限没有通过，借助两数之和的启发，可以调整两数之和的函数

        public static Set<List<Integer>> twoSum2(int [] nums,int target){
        Map<Integer,Integer> tmp = new HashMap<>();
        Set<List<Integer>> res = new HashSet<>();
        for(int i = 0; i < nums.length;i++){
            int component = target - nums[i];
            if(tmp.containsKey(component)){
                List<Integer> tt = new ArrayList<>();
                tt.add(component);
                tt.add(nums[i]);
                res.add(tt) ;
            }
            tmp.put(nums[i],i);
        }
        return res;
//        throw new IllegalArgumentException("");
    }
    public List<List<Integer>> threeSum(int[] nums) {
        Map<Integer,Integer> tmp = new HashMap<>();
        Set<List<Integer>> result = new HashSet<>();
        if(nums.length <= 2)return new ArrayList<>(result);
        for(int x:nums){
            if(tmp.containsKey(x))tmp.put(x,tmp.get(x) + 1);
            else tmp.put(x,1);
        }
        // System.out.println(tmp);
        for(int i:nums){
            Set<List<Integer>> res = twoSum2(nums,- i);
            for(List<Integer> x:res){
                    if(x.get(0) == i && x.get(1) == i && tmp.get(i) >= 3
                            || (x.get(0) == i && x.get(1) != i || x.get(1) == i && x.get(0) != 0) &&tmp.get(i) >= 2
                            || !x.contains(i)
                            ){
                        x.add(i);
                        x.sort(new Comparator<Integer>() {
                            @Override
                            public int compare(Integer o1, Integer o2) {
                                return o1.compareTo(o2);
                            }
                        });
                        result.add(x);
                    }

            }
        }
        return new ArrayList<>(result);
    }

permute（全排列）

给定一个没有重复数字的序列，返回其所有可能的全排列

示例:

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

解法一：按索引插入

从前向后遍历数组，如果是第一个元素，则生成一个只包含第一个元素的数组，插入到结果列表中，之后向后遍历，对于每个元素，遍历一遍结果列表，对于结果列表中的每个列表执行从索引0到最后一位的插入，将新生成的列表插入到结果列表，并且删除上一次遍历产生的结果

    public static List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        for(int i = 0; i < nums.length;i++){
            if(result.size() == 0){
                List<Integer> tmp = new ArrayList<>();
                tmp.add(nums[i]);
                result.add(tmp);
            }else{
                int len = result.size();
                for(int j = 0;j < len;j++){
                    for(int k = 0; k <= result.get(j).size();k++){
                        List<Integer> x = new ArrayList<>(result.get(j));
                        x.add(k,nums[i]);
                        result.add(x);
                    }
                }
                while (len > 0){
                    result.remove(result.get(len - 1));
                    len --;
                }
            }
        }
        return new ArrayList<>(result);
    }

解法二：回溯法（leetcode官方题解）

• 待完成

canJump（跳跃游戏）

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置

示例 1:

输入: [2,3,1,1,4]
输出: true
解释: 从位置 0 到 1 跳 1 步, 然后跳 3 步到达最后一个位置。
示例 2:

输入: [3,2,1,0,4]
输出: false
解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置

解法一：越不过去的0

如果数组全是大于0的数，那么肯定能到达，到不了的地方就是由于某个最大跳跃长度是0的位置无法越过去，即该位置前面不存在一个位置，直接之后调到为0位置的后面

    public static boolean canJump1(int[] nums) {
        if(nums.length <= 1)return true;
        for(int i = nums.length - 2; i >= 0;i--){
            if(nums[i] == 0 && !jumpZero(Arrays.copyOfRange(nums,0,i),i)){
                return false;
            }
        }
        return true;

    }

    public static boolean jumpZero(int[] nums,int index){
        for(int i = nums.length - 1; i >= 0;i--){
            if(nums[i] > index - i)return true;
        }
        return false;
    }

思路二：递归

时间超出限制

    public static boolean canJump(int[] nums) {
        if(nums.length <= 1)return true;
        for(int i = 0; i < nums.length - 1;i++){
            if(canJump(Arrays.copyOfRange(nums,0,i + 1)) && nums[i] >= (nums.length - 1 - i)){
                return true;
            }
        }
        return false;

    }

hasCycle（环形链表）

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环

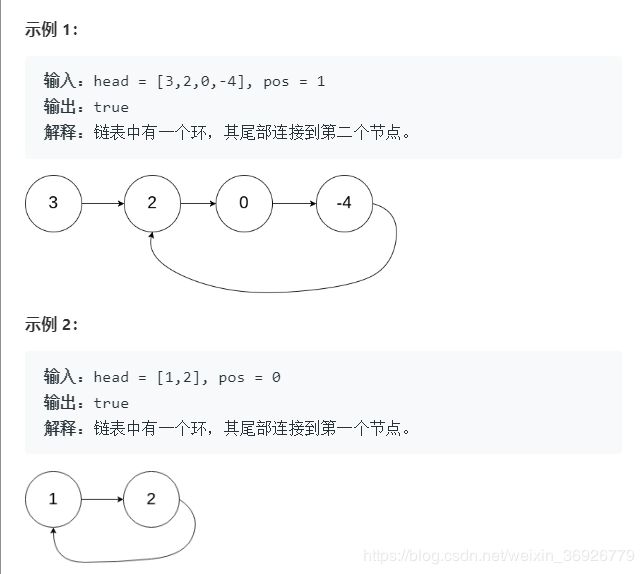
解法一：快慢指针

定义两个快慢指针，一个一次走两步，一个一次走一步，如果有环，指针迟早能相遇

    public static boolean hasCycle1(ListNode head) {
        if(head == null)return false;
        if(head.next == null) return false;
        ListNode p = head.next;
        ListNode q = head;
        while (true){
            if(p.next == q)return true;
            else{
                if(p.next != null && p.next.next != null){
                    q = q.next;
                    p = p.next.next;
                }else{
                    return false;
                }
            }
        }
    }

解法二：重复的引用

遍历链表将每个节点的引用放在哈希集合中，如果已经存在该引用，则说明存在环

    public boolean hasCycle(ListNode head) {
        Set<ListNode> nodesSeen = new HashSet<>();
        while (head != null) {
            if (nodesSeen.contains(head)) {
                return true;
            } else {
                nodesSeen.add(head);
            }
            head = head.next;
        }
        return false;
    }

detectCycle（环形链表II）

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表

解法一：重复的引用

由上面一题的解法二，可以非常容易得到结果，第一次出现重复引用的地方就是环形入口

    public ListNode detectCycle(ListNode head) {
        Set<ListNode> nodesSeen = new HashSet<>();
        while (head != null) {
            if (nodesSeen.contains(head)) {
                return head;
            } else {
                nodesSeen.add(head);
            }
            head = head.next;
        }
        return null;
    }

解法二：快慢指针

继承环形链表I的思想，同样利用两个快慢指针，先找到两个指针第一次相遇的点，然后让其中一个指针重新指向头结点，另一个指针从相遇的地方开始遍历，步长都是1，下一次相遇的地方就是入口节点。
详细的推导过程可以看下下面的博客

环形链表II推导过程传送门：环形链表

    public static ListNode detectCycle6(ListNode head) {
        ListNode p = head;
        ListNode q = head;
        while (p != null && p.next != null){
            p = p.next.next;
            q = q.next;
            if(p == q)break;
        }
        if(p == null || p.next == null)return null;
        q = head;
        while (p != q){
            p = p.next;
            q = q.next;
        }
        return p;
    }

下一篇整理java的基础，包括Collections,String,数组,栈和队列