【文章阅读】IoU Loss for 2D/3D Object Detection
Brief
最近在实验中发现，3D检测的精度和cls_loss的关系非常的大，一般来说，按照SECOND的代码训练下降到cls_loss大致为0.8左右时，会有一个不错的效果，在验证集上可以达到0.88左右的精度（对car-easy）而言，但是当loss继续向下降的时候，反而得不到刚好的效果，改了一些网络结构，加了一些特征，发现改结构的效果并不如从特征或者其他方面着手容易，因此研究别人如何通过LOSS来提高论文精度的。
Abstract
- IOU loss在二维中提出是为了缩小训练集合测试集的训练误差。
- 但是目前所有的方法仅仅对
axis-aligned 2D Bboxes有效果，这就对rotated Bboxes的检测任务是没有帮助的。 - 因此作者的贡献是把给出了两个
rotated Bboxes的IOU计算，后续给出了一个可实现的框架。
1. Introduction
- 检测的发展
- 一般来说IOU仅仅是用作NMS的处理，而不是加入到LOSS中。但是和
L1，L2对比起来看，IOU loss有以下的优点：
（1）在计算IOU的时候，把所有的形状信息都考虑进了计算当中
（2）面积计算过程，已经隐含的编码了参数之间的关系，而不是像L1,L2那样把参数当做是独立的形式
（3）IoU指标对于该问题是尺度不变的，适合解决每个参数之间的尺度和范围差异
2. Related Works
2.3. IoU Loss for Object Detection
- 目前的很多检测的架构的Loss函数都是采用的替代IOU的损失函数
- 现在的已有的IOU LOSS都是针对
axis-aligned Bbox设计的
理解
e axis-aligned Bbox，表示的含义就是和边界是平行的，就是二维检测的检测框都是和二维图片边界平行的意思。但是在3维中，这是一个很困难的方法，因为这是旋转的。
3. IoU for Object Detection
IOU 的另外一个名字叫Jaccard index，其计算公式为：
IoU ( A , B ) = A ∩ B A ∪ B = A ∩ B ∣ A ∣ + ∣ B ∣ − A ∩ B \operatorname{IoU}(\mathbf{A}, \mathbf{B})=\frac{\mathbf{A} \cap \mathbf{B}}{\mathbf{A} \cup \mathbf{B}}=\frac{\mathbf{A} \cap \mathbf{B}}{|\mathbf{A}|+|\mathbf{B}|-\mathbf{A} \cap \mathbf{B}} IoU(A,B)=A∪BA∩B=∣A∣+∣B∣−A∩BA∩B
很好理解，也就是交集部分除以并集
3.1. IoU Definition for Object Detection
转化到3D检测中的IOU计算 ，也就是对于gt： B g B_g Bg和预测框: B d B_d Bd的IOU计算为：
IoU ( B g , B d ) = Aera of overlap B g and B d Aera of union B g and B d \mathbf{\operatorname { I o U }}\left(\mathbf{B}_{g}, \mathbf{B}_{d}\right)=\frac{\text { Aera of overlap } \mathbf{B}_{g} \text { and } \mathbf{B}_{d}}{\text { Aera of union } \mathbf{B}_{g} \text { and } \mathbf{B}_{d}} IoU(Bg,Bd)= Aera of union Bg and Bd Aera of overlap Bg and Bd
- 作者为了引入3D iou,先引入了二维的进行介绍。
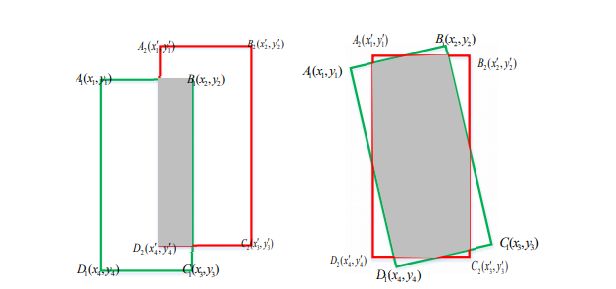
上图均是二维的情形，其中左图表示的是在
axis-aligned的情形，右图是二维中rotated bounding boxes的情形
3.2. Axis-aligned BBox
对于axis-aligned的情形，作者给出的计算步骤如下，不做过多解释，很简单。
3.3. Rotated BBox
我们所要关心的问题也是，rotat-iou是如何计算的
作者这里提到了两中计算IOU的策略：
- 将3D框投影到BEV视角下（在我研究的代码中也是如此做的）
- 直接计算3D的IOU
作者这里优先考虑2D情形，最后考虑3D的情形实际就是给加上一个高度维度进行类似的计算。
如下是针对上图中的二维rotated bounding boxes的情形的IOU计算：
（1）计算gt的面积，也就是先计算两点之间的距离，然后再通过长×宽的方式求得gt的面积
（2）计算预测框的面积：同样的方式。
（3）确定重叠区域的顶点。
（4）按逆时针顺序对这些多边形顶点进行排序
（5）计算overlap
这里的核心就是该如何确定交点和根据交点得到相交的面积。但是作者还没有在文章中给出比较清晰的方法，需要进一步研究代码（下一个工作吧）
一旦有了这样的二维上的旋转的IOU计算公式，那么我们只需要乘以一个高度就得到的对应的IOU
I O U 3 D = Area overlap × h overlap ( Area g × h g + A r e a d × h d − A r e a overlap × h overlap ) \mathbf{I}_{\mathbf{O}} \mathbf{U}_{3 D}=\frac{\text { Area overlap } \times h_{\text {overlap }}}{\left(\text { Area }_{g} \times h_{\mathrm{g}}+\mathbf{A r e a}_{d} \times h_{\mathrm{d}}-\mathbf{A r e a}_{\text {overlap }} \times h_{\text {overlap }}\right)} IOU3D=( Area g×hg+Aread×hd−Areaoverlap ×hoverlap ) Area overlap ×hoverlap
这也就很好的解释了很多的代码中计算IOU为什么直接转移到BEV下进行计算
4. IoU Loss for 2D/3D BBox Regression
上面我们知道了应该如何求的IOU LOSS，但是最重要的是我们应该怎么把这个IOU当做LOSS来计算。
4.1. IoU as Loss
和很多前人在axis-aligned的工作一样，作者定义IOU LOSS如下：这是因为实际上IOU的值是介于0~1，因此就这么设计了。（有一点太简单了8.。。。）
L I O U = 1 − I O U \mathbf{L}_{\mathrm{IOU}}=1-\mathbf{IOU} LIOU=1−IOU
4.2. IoU Loss Layer
作者为此IoU loss layer实现了Forward和backward操作。
这是个啥去？我的理解就是前馈就是计算LOSS，backward应该是通过LOSS更新对应的一些参数。？
4.2.1 Forward
也就是上面那个计算的表格
4.2.2 Backward
这里的主要内容正是反向传播的内容，作者提到大部分的LOSS的反向传播已经可以通过通用框架实现，但是IOU LOSS比较特殊，因此不是很容易实现，作者在后续会把这个项目开源出来（开始期待）
5. Experimental Results
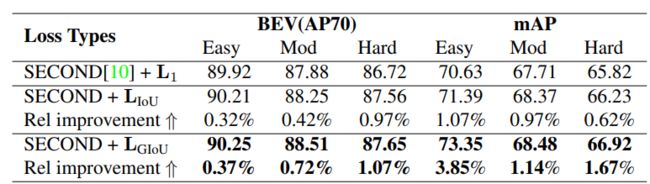
SECOND
在SECOND上加IIOU LOSS，在验证集上的测试：
都是针对的
car的检测效果，同时APnum表示最少大于多少的IOU。
在SECOND上加IIOU LOSS，在测试集的测试：
都是car,不过一个是bev,一个是3D
PointRCNN
和总的实验效果
