Leetcode一起攻克搜索(BFS,DFS,回溯,并查集)
文章目录
- BFS简介
- DFS简介
- 回溯简介
- 并查集简介
- DFS题目
- 690. 员工的重要性
- 1.dfs解法:
- 2.bfs算法
- 547.朋友圈
- dfs解法
- 200.岛屿数量
- dfs解法
- 417.太平洋大西洋水流问题
- dfs解法
- 130.被围绕的范围
- dfs解法
- 733.图像渲染
- dfs解法
- 1020.飞地的数量
- dfs解法
- 841. 钥匙和房间
- dfs解法
- 1034. 边框着色
- dfs解法
- 851. 喧闹和富有
- dfs解法
- 542. 01矩阵
- dfs解法
- 533.孤独像素二(未完成)
- dfs解法
- 394. 字符串解码
- dfs解法
- 339. 嵌套列表权重和
- 思路
- 代码
- 364. 加权嵌套序列和 II
- 思路
- 代码
- 1254. 统计封闭岛屿的数目
- 思路
- 代码
- 回溯题目
- 980. 不同路径 III
- dfs+回溯
- 679.24点游戏
- dfs解法
- 488.祖玛游戏
- dfs解法
- 37.解数独
- 51. N皇后
- 并查集题目(暂未补充)
BFS简介
参考链接
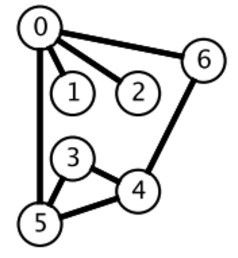
广度优先搜索一层一层地进行遍历,每层遍历都以上一层遍历的结果作为起点,遍历一个距离能访问到的所有节点。需要注意的是,遍历过的节点不能再次被遍历。
第一层:
0->{1,2,6,5}
第二层:
6->{4}
5->{3,4}
第三层:
3->{}
4->{}
每一层遍历的节点都与根节点距离相同。设 di 表示第 i 个节点与根节点的距离,推导出一个结论:对于先遍历的节点 i 与后遍历的节点 j,有 di <= dj。利用这个结论,可以求解最短路径等 最优解 问题:第一次遍历到目的节点,其所经过的路径为最短路径。应该注意的是,使用 BFS 只能求解无权图的最短路径,无权图是指从一个节点到另一个节点的代价都记为 1。
在程序实现 BFS 时需要考虑以下问题:
- 队列:用来存储每一轮遍历得到的节点;
- 标记:对于遍历过的节点,应该将它标记,防止重复遍历。
DFS简介
深度优先遍历顾名思义就是可着一条路去遍历。以下图举例,程序会优先去走一条路,比如会先a->b->e;之后以程序语言来说就是e是叶子节点了,所以结束递归,返回b的位置,此时b会取遍历f,路径就是a->b->f,之后就是返回a,a->c,a->d。其实上述描述语言为前序遍历,当前->左->右。

在程序实现 DFS 时需要考虑以下问题:
栈:用栈来保存当前节点信息,当遍历新节点返回时能够继续遍历当前节点。可以使用递归栈。
标记:和 BFS 一样同样需要对已经遍历过的节点进行标记。
回溯简介
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就 “回溯” 返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为 “回溯点”。许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
回溯算法的基本思想是:从一条路往前走,能进则进,不能进则退回来,换一条路再试。
并查集简介
DFS题目
690. 员工的重要性
题目链接。本题需要考虑的就是不是直系下属的重要程度也需要考虑入内。
1.dfs解法:
dfs的思路就是一条路一条路的去走。
以该例子举例
[[1,5,[2,3]],[2,3,[4]],[3,4,[]],[4,1,[]]]
1
程序的流程是:首先找到员工1,之后找到直系下属员工2,之后找到非直系下属4,最后在非直系下属4的时候结束寻找。也就是传递的始终是当前要找的员工id。
路径为:1->2->4,1->3。
/*
// Employee info
class Employee {
// It's the unique id of each node;
// unique id of this employee
public int id;
// the importance value of this employee
public int importance;
// the id of direct subordinates
public List subordinates;
};
*/
class Solution {
//不是直系下属的也需要添加进去。
int impo;
public int getImportance(List<Employee> employees, int id) {
//还是dfs最好用我觉得
//id与对应的员工信息
Map<Integer,Employee>map = new HashMap<>();
for(Employee e:employees)
map.put(e.id,e);
dfs(map,id);
return impo;**加粗样式**
}
public void dfs(Map<Integer,Employee>map,int id)
{
Employee e = map.get(id);
impo += e.importance;
for(Integer i:e.subordinates)
{
dfs(map,i);
}
return ;
}
}
2.bfs算法
bfs算法是一层一层的遍历。
以该例子举例
[[1,5,[2,3]],[2,3,[4]],[3,4,[]],[4,1,[]]]
1
程序的流程是,一层一层的去遍历,首先遍历的是我们要找的父员工,然后去遍历父员工的所有直系下属员工,之后遍历所有直系下员工的所有直系下属员工。也就是说每一回遍历传递的是一个列表,列表中存储当前层的所有id。
路径为:
第一层:1;
第二层:2,3;
第三层:4。
/*
// Employee info
class Employee {
// It's the unique id of each node;
// unique id of this employee
public int id;
// the importance value of this employee
public int importance;
// the id of direct subordinates
public List subordinates;
};
*/
class Solution {
//不是直系下属的也需要添加进去。
int impo;
public int getImportance(List<Employee> employees, int id) {
//还是dfs最好用我觉得
//id与对应的员工信息
Map<Integer,Employee>map = new HashMap<>();
for(Employee e:employees)
map.put(e.id,e);
List<Integer>list = new ArrayList<>();
list.add(id);
bfs(map,list);
return impo;
}
public void bfs(Map<Integer,Employee>map,List<Integer>l)
{
List<Integer>list=new ArrayList<>();
for(Integer i:l)
{
Employee e = map.get(i);
impo+=e.importance;
list.addAll(e.subordinates);
}
if(list.size()!=0)
bfs(map,list);
return ;
}
}
547.朋友圈
题目链接
dfs解法
这道题我的思路就是深度优先遍历。其实是两层遍历,第一层是遍历每个学生,第二层是遍历每个学生和他有好友关系的学生。第一层的含义其实是循环一次就代表一个朋友圈,因为我们要做的是有记忆功能的dfs。我们使用一个boolean型数组来存储,flag【i】代表i是否已经在一个朋友圈里了。当该学生不在朋友圈中,此时进入dfs递归。在dfs中我们去把该学生的好友关系挨个寻找一遍,以此类推,直到学生的好友关系的那些好友都已经在某个朋友圈当中了。
首先要理解第一个循环走一次就代表一个朋友圈,因为我会在这一次里把所有与该A学生有关的学生全部找到(不是直接有关系,有间接关系的也会找到),这些都在一个朋友圈内。下一次去找的学生是与他们一点关系都没有的学生,然后和这个学生有关系的学生们会组成另一个朋友圈。所以第一个循环走几次就代表有几个朋友圈。
其次,dfs中会遇到两个误导。
1.是否可以从(M【i】数组)i位置往后走,因为i位置以前的学生我都看过了。
答案是否定的。因为比如有四个学生。有可能第一个学生和第二个学生没关系,和第三个学生有关系,那么我们去找第三个学生的时候,就直接去看第三个和第四个学生是否有关系,那万一第三个和第二个学生还有关系呢?
更改做法:所以我们每次都必须从0开始往后找。
2.是否可以在dfs后再将flag【j】赋值为true呢?
答案是否定的。设想第二个学生和第三个学生有关系,那么我们会在M【2】数组的第三个位置进入dfs循环,之后又会在M【3】数组的第二个位置进入上一个dfs循环,这样就会一直循环。
**更改做法:**我们在进入dfs的时候将flag【i】设为true,因为我们是从i学生走过来的,所以我们要将i学生放入我们的朋友圈。
class Solution {
int circles = 0;
//有存储记忆
boolean[]flag;
public int findCircleNum(int[][] M) {
//代表i是否已经在一个朋友圈了
flag = new boolean[M.length];
for(int i=0;i<M.length;i++){
if(flag[i])
continue;
//循环几次就是有几个朋友圈(因为能循环,就代表这个学生没有被加入到朋友圈之中)
circles++;
dfs(M,flag,i);
}
return circles;
}
public void dfs(int[][]M,boolean[]flag,int i) {
//列i之前的不用看了,肯定都看过了。
//因为i行之前的行都看过了。
//要看i学生,是否能和后面的学生继续互为朋友关系。
//上面的是错的,因为比如有四个学生
//有可能第一个学生和第二个学生没关系,和第三个学生有关系,
//那么我们去找第三个学生的时候,就直接去看第三个和第四个学生是否有关系,那万一第三个和第二个学生还有关系呢?
//我们把第i个同学加进我们的朋友圈。
flag[i]=true;
for(int j=0;j<M[0].length;j++)
{
if(flag[j]||i==j)
continue;
if(M[i][j]==1)
{
dfs(M,flag,j);
//这会导致我们一直在dfs循环中,比如第二个和第三个有关系,那么第三个也和第二个有关系。
//就会不断的循环dfs(M,flag,1),和dfs(M,flag,2),去dfs一次就应该把当前循环的那个
//学生加入到朋友圈之中,但不能再dfs之后,应该在dfs初始就加入,防止陷入死循环。
//flag[j]=false;
}
}
}
}
200.岛屿数量
题目链接
本题实在是与朋友圈太像了,与陆地相连的陆地都算是一个岛屿中的陆地,找到数组中所有的岛屿。
dfs解法
使用具有记忆性的dfs。同样是首先循环判断数组中的每个值,当我们发现一个值为1,且他没有被寻找过,那我们就进入dfs递归。在dfs递归中,我们去继续判断该位置的上下左右位置。递归的结束条件是当位置越界或者该值为0(水)或该值被访问过了。
最后判断第一次循环中,走了多少else分支,就代表有多少个岛屿。具体见代码。
class Solution {
//尝试dfs
//其实思路就是当找到一个1后,就将所有与其垂直与水平连通(直接与间接)的1放一起组成岛屿,
//然后看有多少个这样的岛屿
char[][]grid;
//必须带有记忆性
boolean [][]flag;
int rows;
int columns;
public int numIslands(char[][] grid) {
this.grid = grid;
//防止有空
if(grid==null||grid.length==0)
return 0;
rows = grid.length;
columns = grid[0].length;
flag = new boolean [rows][columns];
int island=0;
for(int i=0;i<rows;i++)
{
for(int j=0;j<columns;j++)
{
if(flag[i][j]||grid[i][j]=='0')
continue;
//能执行几次该语句就说明有多少个独立的岛屿
else{
island++;
dfs(i,j);
}
}
}
return island;
}
public void dfs(int i,int j)
{
//判断越界以及是否为水以及是否已经判断过。
if(i<0||i>=rows||j<0||j>=columns||grid[i][j]=='0'||flag[i][j])
return ;
//该值找过了
flag[i][j]=true;
//水平垂直方向
dfs(i-1,j);
dfs(i+1,j);
dfs(i,j-1);
dfs(i,j+1);
}
}
417.太平洋大西洋水流问题
题目链接。
要找到一个位置,它既可以将水流流到太平洋也可以流到大西洋。从位置(i,j)流动到(k,t)的条件为matrix[i][j]>=matrix[k][t]。

dfs解法
- 最初的想法是对每个位置去判断是否可以到达太平洋或者大西洋,后来想到这样递归的时间成本太大,所以最后思路是从太平洋(第一行和第一列)和大西洋的海岸(最后一行,最后一列)开始往陆地去寻找。
- 使用两个boolean数组来存放该位置是否可以到达大西洋/太平洋
- 需要注意的就是dfs要传入四个参数,前两个为位置i和j,第三个为对应海洋的数组,第四个为一个高度值第四个代表的是什么呢,可以理解为当前位置对应的高度值,只有大于等于该高度值才可以满足该位置能够到达对应海洋。
- 当所有海洋的边界(以及可到达海洋边界的点)都递归结束后,可以循环所有点了,将同时满足两个数组的值添加进list。
- 本算法的好处是节省时间。以上述例子的第二行来举例:32344,如果以正常每个位置都判断的算法,会判断3,判断2,判断3,判断4,判断4,而2,3,4,4还会继续向左判断。如果以我们的算法判断,在判断到2的时候就会停止判断,因为2<3,后面的水都无法从这里走到3。
class Solution {
//原本思路是需要从大陆判断到海洋边界(每一块陆地去判断能否到达太平洋和大西洋)
//后来发现可能会超时,那我们从海洋边界逆向判断吧。
int[][]matrix;
int rows;
int columns;
public List<List<Integer>> pacificAtlantic(int[][] matrix) {
List<List<Integer>>results = new ArrayList<>();
this.matrix=matrix;
if(matrix==null||matrix.length==0)
return results;
rows = matrix.length;
columns = matrix[0].length;
//是否能到达太平洋
boolean[][]tai = new boolean[rows][columns];
//是否能到达大西洋
boolean[][]da = new boolean[rows][columns];
//第一行最后一行
for(int j=0;j<columns;j++)
{
dfs(0,j,tai,-1);
dfs(rows-1,j,da,-1);
}
//第一列,最后一列
for(int i=0;i<rows;i++)
{
dfs(i,0,tai,-1);
dfs(i,columns-1,da,-1);
}
for(int i=0;i<rows;i++)
{
for(int j=0;j<columns;j++)
{
if(tai[i][j]&&da[i][j])
{
List<Integer>list = new ArrayList<>();
list.add(i);
list.add(j);
results.add(list);
}
}
}
return results;
}
//传入4个参数,前两个为当前位置,flag为存储能否到达当前洋的数组,last是上一个值(也是能到达flag海岸的最小值)
public void dfs(int i,int j,boolean[][]flag,int last)
{
//越界
if(i<0||i>=rows||j<0||j>=columns||matrix[i][j]<last)
return ;
//已经可以达到了。
if(flag[i][j])
return;
flag[i][j]=true;
dfs(i,j+1,flag,matrix[i][j]);
dfs(i,j-1,flag,matrix[i][j]);
dfs(i+1,j,flag,matrix[i][j]);
dfs(i-1,j,flag,matrix[i][j]);
}
}
130.被围绕的范围
题目链接
本题乍一看会不明白题目要搞锤子?什么样的O要换成X呢,难道我要判断每个O的四周是不是都是X?
其实核心在这里:被围绕的区间不会存在于边界上,换句话说,任何边界上的 ‘O’ 都不会被填充为 ‘X’。 任何不在边界上,或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
其实是要找到所有与边界上的’O’以及与边界上‘O’相连的’O’,这些’O’不被填充为X,其他的O全部填充为X,那么这样就好解决了。
dfs解法
对四个边角分别进行dfs递归。同时更改在边界上以及与边界上O相连的O为‘b’,最后去数组判断,将为b的改回O,为O的改成X。
class Solution {
//解释中写道任何不在边界上,或不与边界上的‘o’相连的‘o’最终都会被填充为‘x’
//本题可以转化为寻找与边界'o'连通(水平与垂直)的'o'
char[][]board;
int rows;
int columns;
public void solve(char[][] board) {
this.board = board;
if(board==null||board.length==0)
return ;
rows = board.length;
columns = board[0].length;
//第一行和最后一行
for(int i=0;i<board[0].length;i++)
{
dfs(0,i);
dfs(rows-1,i);
}
//第一列和最后一列
for(int j=0;j<board.length;j++)
{
dfs(j,0);
dfs(j,columns-1);
}
//将所有不与边界o连通的o换成x。
//将之前更改过的o也改回去
for(int i=0;i<rows;i++)
{
for(int j=0;j<columns;j++)
{
if(board[i][j]=='b')
board[i][j]='O';
else if(board[i][j]=='O')
board[i][j]='X';
}
}
}
public void dfs(int i,int j)
{
if(i<0||i>=rows||j<0||j>=columns||board[i][j]=='X'||board[i][j]=='b')
return ;
board[i][j]='b';
dfs(i,j-1);
dfs(i,j+1);
dfs(i-1,j);
dfs(i+1,j);
}
}
733.图像渲染
题目链接
dfs解法
本题比较简单。
class Solution {
int[][]image;
int rows;
int columns;
int oldColor;
public int[][] floodFill(int[][] image, int sr, int sc, int newColor) {
//还有一个条件是与初始位置的像素值相同
this.image = image;
if(image==null||image.length==0)
return image;
rows = image.length;
columns = image[0].length;
oldColor = image[sr][sc];
dfs(sr,sc);
for(int i=0;i<rows;i++)
{
for(int j=0;j<columns;j++)
{
if(image[i][j]==-1)
image[i][j]=newColor;
}
}
return image;
}
public void dfs(int sr,int sc)
{
if(sr<0||sr>=rows||sc<0||sc>=columns||image[sr][sc]==-1||image[sr][sc]!=oldColor)
return ;
image[sr][sc]=-1;
dfs(sr+1,sc);
dfs(sr-1,sc);
dfs(sr,sc+1);
dfs(sr,sc-1);
}
}
1020.飞地的数量
题目链接
dfs解法
这题和之前的题类似,也是从边界开始找,我们找到所有与边界的1所连通的1。将这些1更改为-1,之后遍历数组,统计数值仍然为1的数量,就是无法离开的陆地。
class Solution {
int[][]A;
int rows;
int columns;
public int numEnclaves(int[][] A) {
//找到所有与边界1连接的1,统计其他1的数量
this.A = A;
int numbers = 0;
if(A==null||A.length==0)
return 0;
rows = A.length;
columns = A[0].length;
//第一列和最后一列
for(int i=0;i<rows;i++)
{
dfs(i,0);
dfs(i,columns-1);
}
//第一行和最后一行
for(int j=0;j<columns;j++)
{
dfs(0,j);
dfs(rows-1,j);
}
for(int i=0;i<rows;i++)
{
for(int j=0;j<columns;j++)
{
if(A[i][j]==1)
numbers++;
}
}
return numbers;
}
public void dfs(int i,int j)
{
if(i<0||i>=rows||j<0||j>=columns||A[i][j]==0||A[i][j]==-1)
return;
A[i][j]=-1;
dfs(i-1,j);
dfs(i+1,j);
dfs(i,j+1);
dfs(i,j-1);
}
}
841. 钥匙和房间
题目链接
dfs解法
本题要看能不能把所有的房间遍历一遍,也需要使用记忆性dfs,使用一个boolean数组来存储该房间是否走过,使用一个变量代表可以去的房间的数量,在dfs中,遍历当前房间中的钥匙列表,直到完成dfs。
class Solution {
List<List<Integer>>rooms;
boolean[]flags;
//可以去的房间数
int canRooms = 0;
public boolean canVisitAllRooms(List<List<Integer>> rooms) {
this.rooms = rooms;
if(rooms == null||rooms.size()==0)
return true;
int nums = rooms.size();
flags = new boolean[nums];
dfs(0);
if(canRooms==nums)
return true;
else
return false;
}
public void dfs(int index)
{
//到这里代表i房间我们已经去过惹
flags[index]=true;
canRooms++;
List<Integer>keys = rooms.get(index);
for(int i=0;i<keys.size();i++)
{
//已经可以就不去
if(flags[keys.get(i)])
continue;
dfs(keys.get(i));
}
}
}
1034. 边框着色
题目链接
我先说下我对于DFS的理解,我觉得应该在到达边界之后不应该结束DFS,因为其上下左右可能还有连通分量,应该继续去走。本题不需要多余的数组去存储我们更改的位置,直接使用原始的数组即可。不过我们需要记录我们走过的位置,走过的位置我们就不走了。
我简单说下我DFS的思路,首先判断是否越界,越界返回-1,(1代表该位置的值不是连通分量的值,也就是该位置上下左右的连通分量为连通分量边界,-1为其他)。之后先判断该位置的值是否被更改过,如果被更改过就可以直接返回-1,如果不是在这一分支,说明该值要么可能没走过要么可能走过了但该值不等于连通分量中的值,假如该值不为连通分量的值,那么我们就要返回1,不管其是否走过,之后不处于这个分支,就只能是没走过的连通分量支或走过的连通分支但没有被更改,只要是走过的我们就应该返回-1。核心思路就是留下我们没走过的连通分量,之后去该位置的上下左右,之后去判断该位置是否为第一/最后一行或者第一/最后一列,如果是直接可以更改该位置的值为color,如果不是的话就去判断该位置是否为边界(上下左右是否有一个为1)。结束判断。
讲一下为什么是这个逻辑,假如我们先判断该值不等于oldColor,那么该值可能之前等于,但后来更改了就变成了不等于oldColor,这样返回1就是错误的。之后还有第二个分支为什么要在前面,不管该值我们遍历没遍历过,只要原本就不等于oldColor,我们就会返回1,他旁边的连通分量就是连通分量的边界。
dfs解法
class Solution {
int[][]grid;
boolean[][]flag;
int rows;
int columns;
int oldColor;
int color;
public int[][] colorBorder(int[][] grid, int r0, int c0, int color) {
this.color = color;
this.grid = grid;
if(grid==null||grid.length==0)
return grid;
oldColor = grid[r0][c0];
rows = grid.length;
columns = grid[0].length;
flag = new boolean[rows][columns];
dfs(r0,c0);
return grid;
}
public int dfs(int i,int j)
{
//不能先判断flag[i][j]再判断grid[i][j]!=oldColor,
//这样有一个bug(比如第二行的第四个1,是连通分量的边界(上面是2),但可能这个2已经走过了,这样先判断flag[i]就会跳出去了)
//比如21221
// 11111
// 22212
// 12212
// 21112
//r0=1,c0=4,也就是oldColor=1。
if(i<0||i>=rows||j<0||j>=columns)
return -1;
//防止该值被更改过了值
if(flag[i][j]&&grid[i][j]==color)
return -1;
//不管遍历没遍历过只要该值本来就不是连通分量的值,就返回1。
else if(grid[i][j]!=oldColor){
return 1;
}//如果该遍历过了,不再继续遍历了。
else if(flag[i][j])
return -1;
flag[i][j] = true;
//边界(要涂色)
int d = dfs(i+1,j);
int u = dfs(i-1,j);
int r = dfs(i,j+1);
int l = dfs(i,j-1);
if(i==0||j==0||i==rows-1||j==columns-1)
{
grid[i][j] = color;
}
else if(d==1||u==1||r==1||l==1)
{
grid[i][j] = color;
}
return -1;
}
}
851. 喧闹和富有
题目链接
dfs解法
如果 y 比 x 富有,考虑带有边 x -> y 的有向图。对于每个人(person x),我们都希望最安静的人就在 x 的子树中。
因此我们为每个人(person)设置列表,包含比他有钱的人,每一个列表其实为一个有向图。
构建上面所描述的图,并且称 dfs(person) 是 person 的子树上最安静的人。注意,因为语句在逻辑上是一致的,所以图必须是有向无环图(即,DAG)—— 任意一条边有方向,且不存在环路的图。
现在 dfs(person) 可以是 person,或者是 min(dfs(child))。也就是说,子树中最安静的人可以是 person 本身,或者是 person 的孩子结点的某个子树中最安静的人。
当执行图的 后序遍历 时,我们可以将 dfs(person) 的值作为 answer [person] 缓存。
这里dfs第一次返回的是在当前这个person没有人(肯定)比他更有钱了,那么他的answer就是他自己。
class Solution {
//给每个人设置个列表,代表比他有钱的人的编号(其实为有向图(好多个分支),而x->y则代表x没有y富有)
//最安静的是quiet[i]中最小的。
ArrayList<Integer>[]richMap;
//另设置一个数组代表这个人是否已经判断完比他有钱的人中最安静的人。
int[]answers;
//总人数
int N;
public int[] loudAndRich(int[][] richer, int[] quiet) {
N = quiet.length;
richMap = new ArrayList[N];
answers = new int[N];
//防止这个人(i)的最安静且比他有钱的人就是0。
Arrays.fill(answers,-1);
for (int node = 0; node < N; ++node)
richMap[node] = new ArrayList<Integer>();
for (int[] edge: richer)
richMap[edge[1]].add(edge[0]);
//每个人都得dfs一次
for(int i=0;i<N;i++)
dfs(quiet,i);
return answers;
}
//这里需要返回比这个人富有且最安静的人的编号()
public int dfs(int[]quiet,int person)
{
if(answers[person]==-1)
{
List<Integer>richers = richMap[person];
int Maxperson = person;
if(richers!=null)
{
for(int richer:richers)
{
int Quietestperson = dfs(quiet,richer);
Maxperson =quiet[Quietestperson]<quiet[Maxperson]?Quietestperson:Maxperson;
}
}
answers[person] = Maxperson;
}
return answers[person];
}
}
542. 01矩阵
题目链接
dfs解法
本题的思路就是先把0加入队列,然后去影响周围的元素,之后把1加入队列,继续去影响周围的元素。。。。
class Solution {
public int[][] updateMatrix(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
Queue<int[]> q = new LinkedList<>();
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++) {
// 把0元素加入队列中,以备波及影响周围元素
if (matrix[i][j] == 0)
q.offer(new int[] { i, j });
else
// 设为最大值,方便求0元素影响值
matrix[i][j] = Integer.MAX_VALUE;
}
// 上下左右
int[][] dirs = { { -1, 0 }, { 1, 0 }, { 0, -1 }, { 0, 1 } };
while (!q.isEmpty()) {
int cell[] = q.poll();
for (int[] d : dirs) {
int row = cell[0] + d[0];
int col = cell[1] + d[1];
if (row < 0 || row >= m || col < 0 || col >= n)
continue;
// 上下左右取到的值
int value = matrix[row][col];
int tmp = matrix[cell[0]][cell[1]] + 1;
// 如果value小,那说明之前已经更新过,不是max
if (value <= tmp)
continue;
q.offer(new int[] { row, col });
matrix[row][col] = tmp;
}
}
return matrix;
}
}
533.孤独像素二(未完成)
题目链接
dfs解法
394. 字符串解码
题目链接
dfs解法
本题比较复杂的就是要考虑括号中套括号的情况,其实遇到这种情况第一反应就是要使用栈来进行解答。使用两个栈,一个用来存储数字,另一个用来存储当前的字符串(当遇到‘[‘时存入,当遇到]时要弹出与【】内的字符串组成新的字符串)。下面的代码写了遇到四种情况。
接下来来个例子:"3[a]2[b4[F]c]"
1:数字3。3入栈此时,num=3,numStack = “”, StringStack = “”;
2:左括号。将num入栈,将sb入栈,num=0,numStack = 3, StringStack = “”
3.: a。将字母添加进sb,其他不变,sb为a
4.右括号。将【】中的与之前的字符串(字符串栈中)组合起来,newString = aaa,oldString = “”;
sb=aaa,
一个坑:这里我想大家就会有个疑问了,为什么在遇到左括号时清空num,而不是在右括号之后清空num呢。
考虑这个例子:“2[ab3[cd]]4[xy]”,如果不在遇到左括号时就将数字清空,当我们到第二个左括号时,num已经变成了23,所以需要遇到左括号就清空一下num,也符合我们的题意,num后面就会紧跟着【】,所以这个num只和【】中的字母有关系。下次在遇到【】时,必须要让【】只匹配他前面,再往前的不匹配。所以要遇到【,就要将num清空。
第二个坑:为什么我们不在遇到右括号处理之后就把结果压入栈中呢,理由如下:因为我们只有遇到左括号才能说明,当前的sb是与后面的左括号以后的字符串是并列关系,只有这时才会分oldString与newString。
话不多说我们继续往下走
5.数字2,num = 2,numStack = “”,StringStack =“”,
6.左括号,numStack=2,sb入栈,StringStack=aaa,num=0,sb=“”
7.b,sb=b,其他不变
8.4,num=4,其他不变
9.左括号,numStack={2,4},StringStack={aaa,b},sb=“”,num=0
10.F,sb=F,其他不变
11.右括号,numStack出栈,与F组合newString为FFFF(二次元莫名喜感),弹出StringStack的栈顶(b)为oldString,组合之后sb为bFFFF。
12.c,sb=bFFFFc
13.右括号,numStack出栈(2),组合厚度newString就是bFFFFcbFFFFc,oldString为aaa。组合之后为aaabFFFFcbFFFFc。
返回aaabFFFFc。好累,但是这个例子比较好,
class Solution {
//使用两个栈(存储数字和字符串,每次遇到],应该先使用最新的数字,所以使用先进后出的栈)
//有四种情况:
//1.数字:有可能是连续的数字,比如44
//用num存储
//2.左括号[
//1).遇到该字符要将数字入栈,以便用于遇到]时将[]中的字符串进行处理
//2).要将之前累积的sb入栈,用于在之后遇到]时,将新做出来的字符串与之前的字符串拼接起来
//3).要将sb和num清空,要去记录左左括号后面的东西惹
//3.右括号]
//先将数字(最新的)出栈,组成数字*res,之后再将字符串出栈,将旧字符串与新组成的字符串组合到一起,组成sb。
//4.字母
//将字母加入sb
public String decodeString(String s) {
StringBuilder sb = new StringBuilder();
Stack<Integer>numStack = new Stack<>();
Stack<String>StringStack = new Stack<>();
int num = 0;
for(int i=0;i<s.length();i++)
{
char now = s.charAt(i);
if(Character.isDigit(now))
{
//可能是连续的呀
num = num*10+ now-'0';
}
//到了这里要把前面做好的StringBuilder入栈
else if(now == '[')
{
//这里的sb就是从上一个[到这个[的
//比如3【a2【c】】中的a,也是3[a]2[bc]的aaa。
numStack.push(num);
StringStack.push(sb.toString());
//清空sb
sb.delete(0,sb.length());
num = 0;
}
else if(now == ']')
{
String old = StringStack.pop();
String curr = sb.toString();
//本身就有一次了,咱们就让他再往里加num-1次就好
int times = numStack.pop()-1;
for(int j=0;j<times;j++)
{
sb.append(curr);
}
//将old与新的添加进去。old直接放在所有的最前面即可。
sb.insert(0,old);
}
//可能是大写
else
{
sb.append(now);
}
}
return sb.toString();
}
}
339. 嵌套列表权重和
题目链接
思路
这种有括号的其实第一反应是栈,但是后来看到这里涉及了一个新的数据结构NestedInteger,题目中也说到了每个元素要么是整数,要么是列表。同时,列表中元素同样也可以是整数或者是另一个列表。为了验证心中所想,我返回了[[1,1],2,[1,1]]这个list的长度,果然是三,也就是说NestedInteger要么是整数,要么是一个List。那就不需要去找左右括号了,直接判断当前的NestedInteger是list还是整数,是整数就加上当前的数与当前深度的乘积,是list就继续递归(传入这个list与当前深度+1)。在dfs中循环list中的每个值,对每个值都进行如上判断。
代码
/**
* // This is the interface that allows for creating nested lists.
* // You should not implement it, or speculate about its implementation
* public interface NestedInteger {
* // Constructor initializes an empty nested list.
* public NestedInteger();
*
* // Constructor initializes a single integer.
* public NestedInteger(int value);
*
* // @return true if this NestedInteger holds a single integer, rather than a nested list.
* public boolean isInteger();
*
* // @return the single integer that this NestedInteger holds, if it holds a single integer
* // Return null if this NestedInteger holds a nested list
* public Integer getInteger();
*
* // Set this NestedInteger to hold a single integer.
* public void setInteger(int value);
*
* // Set this NestedInteger to hold a nested list and adds a nested integer to it.
* public void add(NestedInteger ni);
*
* // @return the nested list that this NestedInteger holds, if it holds a nested list
* // Return null if this NestedInteger holds a single integer
* public List getList();
* }
*/
class Solution {
int sum=0;
public int depthSum(List<NestedInteger> nestedList) {
dfs(nestedList,1);
return sum;
}
public void dfs(List<NestedInteger> list,int depth)
{
if(list==null||list.size()==0)
return ;
for(int i=0;i<list.size();i++)
{
NestedInteger nested = list.get(i);
if(nested.isInteger())
{
sum+=nested.getInteger()*depth;
}
else{
dfs(nested.getList(),depth+1);
}
}
}
}
364. 加权嵌套序列和 II
思路
有一说一,这个思路我觉得有点丑陋,但是一看题解里都是这么做。这道题的要求和上一道题有些许不同,与前一个问题不同的是,前一题的权重按照从根到叶逐一增加,而本题的权重从叶到根逐一增加。那么我们就先找出他的深度,然后再在之前判断为整数后乘上(总深度-当前深度)即可。注意我的dfs函数设置了一个boolean型变量,以便判断是否求解出了总深度。
代码
/**
* // This is the interface that allows for creating nested lists.
* // You should not implement it, or speculate about its implementation
* public interface NestedInteger {
* // Constructor initializes an empty nested list.
* public NestedInteger();
*
* // Constructor initializes a single integer.
* public NestedInteger(int value);
*
* // @return true if this NestedInteger holds a single integer, rather than a nested list.
* public boolean isInteger();
*
* // @return the single integer that this NestedInteger holds, if it holds a single integer
* // Return null if this NestedInteger holds a nested list
* public Integer getInteger();
*
* // Set this NestedInteger to hold a single integer.
* public void setInteger(int value);
*
* // Set this NestedInteger to hold a nested list and adds a nested integer to it.
* public void add(NestedInteger ni);
*
* // @return the nested list that this NestedInteger holds, if it holds a nested list
* // Return null if this NestedInteger holds a single integer
* public List getList();
* }
*/
class Solution {
int times = 0;
int counts = Integer.MIN_VALUE;
public int depthSumInverse(List<NestedInteger> nestedList) {
//先DFS求出最深的层,然后在一次DFS求解
dfs(nestedList,1,false);
dfs(nestedList,0,true);
return times;
}
public void dfs(List<NestedInteger>nestedList,int deepth,boolean flag)
{
if(nestedList==null||nestedList.size()==0)
{
return ;
}
for(int i=0;i<nestedList.size();i++)
{
NestedInteger now = nestedList.get(i);
if(now.isInteger())
{
if(flag)
times+=(counts-deepth)*now.getInteger();
}else{
dfs(now.getList(),deepth+1,flag);
}
}
counts = Math.max(deepth,counts);
}
}
1254. 统计封闭岛屿的数目
思路
本题和不同的岛屿数量相似,区别在于要求岛屿封闭,该位置如果位于陆地的边界(比如左边界就要其左边必须是1)就要求其所在边界方向上前一个位置要为水(1)。同时本题中有两个隐含条件:1.数组边界外都是陆地。2.第一行第一列最后一行最后一列都不可能包含陆地,因为二维矩阵的边界之外可以理解都是陆地。使用记忆性搜索,但不多用一个boolean数组直接使用grid。本题不涉及回溯。
本题思路就是判断一个位置是否为封闭岛屿就是该位置四个方向返回的都是true,那么什么情况下该方向返回true呢?
以左方向为例,有两种情况,1.该位置的左方向的值为1,说明该位置为岛屿左边界,且左边为水域,则返回true;
2.该位置左方向的值为0,那么说明该位置不是岛屿左边界,左边还有陆地,因此也应该返回true。
理解了上述的话,j就很容易理解下面的话。
本题的一个核心是走过的0要赋值为1。为什么要赋值为1呢,我们假设grid[i,j]=1,那么有哪些位置可能再次访问该位置(i,j)呢,其左边位置(i,j-1)访问其右方向,右边位置(i,j+1)访问其左方向,上边位置(i-1,j)访问其下方向,下边位置(i+1,j)访问其上方向。访问时,都可以看出该位置右/左/下/上方向还有陆地,因此对应该位置的该方向应该返回true,所以就把走过的0都赋值为1。
那么问题又来了,我现在赋值为1会不会影响到第二次大DFS(指第一次大dfs结束,又返回closedIsland的循环中去判断,找到了其他的0,进入第二次大DFS)呢,憨憨一次dfs会把所有连通的0都走一遍,现在走的0是与上一次DFS中的那些0不连通的,那为什么不连通呢,因为中间被水隔开了啊,所以不会影响第二次大DFS的判断。
代码
class Solution {
public int closedIsland(int[][] grid) {
//区别在于要求封闭(假如该位置为陆地的最左边则要求其左边必须是1)
//同时第一行第一列最后一行最后一列都不可能包含陆地,因为二维矩阵的边界之外可以理解都是陆地
//使用记忆性搜索但不多用一个数组了直接用grid
int times = 0;
for(int i=1;i<grid.length;i++)
{
for(int j=1;j<grid[0].length;j++)
{
if(grid[i][j]==0)
{
if(dfs(grid,i,j))
times++;
}
}
}
return times;
}
//对应每个位置要求四个方向返回的都是true,才可以返回true
public boolean dfs(int[][]grid,int i,int j)
{
if(i<0||j<0||i>grid.length-1||j>grid[0].length-1)
return false;
if(grid[i][j]==1)
return true;
//标记走过了
//为什么赋值grid[i][j]为1呢,
//因为当dfs(i,j+1)时,会判断(i,j+1)位置的上下左右位置,而其左位置为dfs(i,j),当前位置(i,j+1)并不是岛屿的最左边界(当j为j-1时为最左边界),因此当前位置左边可以是陆地也可以是水域。所以当我们遇到一个陆地之后就要把他赋值为1,其上边位置的值对应down就为true,其左边位置的值对应right就为true,其下边的值对应up就为true,其右边的值对应left就为true,因为这四个位置的值在对应的这四个方向都不是边界位置。
grid[i][j] = 1;
boolean left = dfs(grid,i,j-1);
boolean right = dfs(grid,i,j+1);
boolean up = dfs(grid,i-1,j);
boolean down = dfs(grid,i+1,j);
return left&&right&&up&&down;
}
}
回溯题目
980. 不同路径 III
dfs+回溯
class Solution {
int [][]grid;
boolean[][]flag;
int rows;
int columns;
int nums;
int starti;
int startj;
int endi;
int endj;
int results=0;
public int uniquePathsIII(int[][] grid) {
this.grid = grid;
if(grid==null||grid.length==0)
return 0;
rows = grid.length;
columns = grid[0].length;
flag = new boolean[rows][columns];
for(int i=0;i<rows;i++)
{
for(int j=0;j<columns;j++)
{
if(grid[i][j]==0)
nums++;
if(grid[i][j]==1)
{
starti=i;
startj=j;
}
if(grid[i][j]==2)
{
endi=i;
endj=j;
}
}
}
dfs(starti,startj,-1);
return results;
}
public void dfs(int i,int j,int counts)
{
//需要回溯
if(i<0||i>=rows||j<0||j>=columns||grid[i][j]==-1||flag[i][j])
return ;
if(i==endi&&j==endj&&counts==nums)
{
results++;
return ;
}
flag[i][j]=true;
dfs(i+1,j,counts+1);
dfs(i-1,j,counts+1);
dfs(i,j-1,counts+1);
dfs(i,j+1,counts+1);
flag[i][j]=false;
}
}
679.24点游戏
题目链接
dfs解法
只有 4 张牌,且只能执行 4 种操作。即使所有运算符都不进行交换,最多也只有 12 * 6 * 2 * 4 * 4 * 4 = 921612∗6∗2∗4∗4∗4=9216 种可能性,这使得我们可以尝试所有这些可能。
具体来说,我们有 12(43) 种方式先选出两个数字(有序),并执行 4 种操作之一(12 * 4)。然后,剩下 3 个数字,我们从中选择 2 个并执行 4 种操作之一(32 * 4)。
最后我们剩下两个数字,并在 2 * 4(有序) 种可能之中作出最终选择。
对于在我们的列表中移除 a, b 这两个数字的每一种方法,以及它们可能产生的每种结果,如 a + b、a / b等,我们将采用递归的方法解决这个较小的数字列表上的问题。
class Solution {
public boolean judgePoint24(int[] nums) {
List<Double>nowNums = new ArrayList<>();
for(int num:nums)
nowNums.add((double)num);
return dfs(nowNums);
}
public boolean dfs(List<Double>nowNums)
{
/*
if(nowNums.size()==0)
return false;
*/
if(nowNums.size()==1)
//浮点数有问题
return (Math.abs(nowNums.get(0)-24)<1e-6);
//当四个的时候,第一次选两个数时有4*3种,之后选运算符为12*4=48,
//然后3个选两个为3*2种,之后选运算符:6*4 = 24;
//最后2个选运算符:2*4种(有先后顺序之分哦)
//不过+和*满足交换律
for(int i=0;i<nowNums.size();i++)
{
for(int j=0;j<nowNums.size();j++)
{
if(i==j)
continue;
List<Double>newNums = new ArrayList<>();
for(int k=0;k<nowNums.size();k++)
{
//不能添加i,j因为i和j所在位置的数接下里我们要进行计算,
if(k!=i&k!=j)
{
newNums.add(nowNums.get(k));
}
}
//+*-/
for(int times = 0;times<4;times++)
{
//加和乘满足交换律
if(times<2&&j>i)
continue;
if(times==0) newNums.add(nowNums.get(i)+nowNums.get(j));
if(times==1) newNums.add(nowNums.get(i)*nowNums.get(j));
if(times==2) newNums.add(nowNums.get(i)-nowNums.get(j));
if(times==3)
{
if(nowNums.get(j)!=0)
newNums.add(nowNums.get(i)/nowNums.get(j));
else
continue;
}
//一路递归找到了结果
if(dfs(newNums)) return true;
//之前添加的那个运算符不行,扔了之前那个结果吧,回溯到之前选择运算符
newNums.remove(newNums.size()-1);
}
}
}
//一个都不行
return false;
}
}
488.祖玛游戏
题目链接
dfs解法
这道题坑太多了
1.本题中dfs其实有两个,第一个是将每个球向指定位置插入,位置可以是从[0,board.length)
2.在每次dfs之前,我们要先判断一下当前字符串中是否有大于等于3个的字符,因为比如:BRRWWRBB,我向WW中放入一个W,之后dfs传入的字符串就变成了了BRRRBB,这其中就包含了RRR,所以需要一个函数去除掉当前字符串中已经大于等于三个的字符(这里涉及一个递归的思想,我去掉RRR之后,就变成了BBB,还需要继续递归,直到找不到相同的,返回这个字符串)
3.为什么findMinStep中判断的结果是
return results==maxBall?-1:results;
我们以"WRRBBW", “RB” 这个为例,如果到了怎么都移除不了的时候,在hands为空的时候或hands中不够的那一次dfs时,会返回maxBall的个数,之后返回上一层dfs时,dfs(i-1)在比较的时候,rs=min(maxBall,maxBall(dfs(i))+needBalls),这里又会返回maxBall,所以直到返回第一层dfs时,都会是rs=min(maxBall,maxBall(dfs(1))+needBalls),最终返回maxBall。所以如果没有办法清除,最终第一层dfs会返回maxBall。
4.dfs的时候,board加上#号的好处,我们不需要考虑走到board中最后一位这种情况。我们让j始终往后跑,去判断是否可以和i的值相等,最后有两种情况:1.字符串为B#,2.字符串为BB#,第一种是j已经走到#号了,i为B,最后i=j,走到#号。第二种情况是j和i都在第一个B处,之后j先走到#,之后i=j时,i和j走到#号。
5.回溯就不用说了,我们在插入该位置去掉手中的这些球,在dfs之后,我们在加回来,因为下一次插球(插入其他位置)可能会用到
代码如下:
class Solution {
//对board中每一个位置去添加手中的球(前提是添加进去可以消除)之后继续递归,直到手中的球全没有了
//去判断是否board为空了
//最大为5个
int maxBall = 6;
public int findMinStep(String board, String hand) {
//用整形数组来存储我们手中球
int[]hands = new int[26];
for(int i=0;i<hand.length();i++)
hands[hand.charAt(i)-'A']++;
//防止出现问题,这个#号加的太精髓了。
int results = dfs(board+"#",hands);
return results==maxBall?-1:results;
}
//如果怎么都移除不了,在hands为空的时候或hands中不够的那一次dfs时,会返回maxBall的个数
//之后返回上一层dfs时,dfs(i-1)在比较的时候,min(maxBall,maxBall(dfs(i))+needBalls),
//这里又会返回maxBall
//所以直到返回第一层dfs时,都会是min(maxBall,maxBall(dfs(1))+needBalls),最终返回maxBall
public int dfs(String board,int []hands)
{
board = removeConsecutive(board);
//全移除了
if(board.equals("#"))
return 0;
int rs = maxBall;
//插入board字符串中的哪一个字符都是可以的哦
//(走到最后的时候,可能是i指向最后一个字母,而j指向了#,然后进行最后一次判断(尝试为最后一个字母填进去2个球),之后i和j一同走向#。
//或者是i和j都指向了最后一个#(之前j不是#,j在本次走到#),然后下一次就会停止循环。
//i永远不会到"#",或者说即使到了下一次j++就出来了
//所以不用担心nowBall不是数组中的index。
for(int i=0,j=0;j<board.length();j++)
{
//看看有几个相同的,必然小于三个
if(board.charAt(i)==board.charAt(j)) continue;
int needBalls = 3-(j-i);
int nowBall = board.charAt(i)-'A';
if(hands[nowBall]>=needBalls)
{
//铁憨憨你在外面拼,那不是下一个i的时候也用你这个board了么
//拼一下(不包含i,包含j)
//board = board.substring(0,i)+board.substring(j);
hands[nowBall]-=needBalls;
//这里不是+1,是加上需要的球
rs = Math.min(rs,dfs(board.substring(0,i)+board.substring(j),hands)+needBalls);
//回溯回去
hands[nowBall]+=needBalls;
}
//这些相同的是一样的,可以直接往后走即可
i=j;
}
return rs;
}
/**
有可能我们将三个球清理之后,又前面后面的碰到一起又超过了三个球
**/
private String removeConsecutive(String board) {
//最后还是会走到j到#,然后i不是#,然后下一次退出。
for (int i = 0, j = 0; j < board.length(); j++) {
if (board.charAt(j) == board.charAt(i)) continue;
if (j - i >= 3) return removeConsecutive(board.substring(0, i) + board.substring(j));
//继续往后看
else i = j;
}
return board;
}
}
37.解数独
题目链接
思路:使用三个数组分别用于存储该行是否包含这个数,该列是否包含这个数,该宫里是否包含这个数,使用一个boolean变量用于判断是否找到了结果。需要先遍历一遍数组,填充上述三个数组,然后进行dfs,dfs的顺序是从左上角到右上角,一个一个遍历(依次向右遍历,如果到了本行最后一个就跳下一行第一个),终止条件就是已经到了第十行,说明前九行已经全部赋值结束。
需要注意的是:
1.以前就有的值我们不能更改,要单独区分一下,这样的位置我们直接向后去判断即可。当我们dfs下一个位置结束后返回到该位置后,也会直接再返回前一个位置。
2.当我们找到结果之后要将boolean变量赋值为true。此时dfs(9,0)就会返回到dfs(8,8),假如(8,8)本身就有值,那么就会继续返回(8,7),我们假设(8,7)本身没有值,是我们后添加的值,那么就会走到如下代码。我们要判断下究竟是(8,7)这个值不合适,还是已经找到了所有数独的解,如果是找到了所有数独的解就直接返回就行了,这样就会一直返回到dfs(0,0)的这里,然后返回。
//这里可能是当前位置不能选取这个数,因为选取完这个数之后下一个位置的数无法找到合适的数
//也可能是当前的i和j下一个位置已经到达终点,然后return,就会走到这里
if(!find){
rows[i][num-1] = false;
columns[j][num-1] = false;
tables[table][num-1] = false;
board[i][j] = '.';
}else{
//如果找到了所有的值,dfs(9,0)就会将find置为true,然后返回dfs(8,8)的if(!find)这里,之后就会继续返回,直到返回dfs(0,0)的这里
return ;
3.返回的两种情况:比如dfs(i,j)没有找到一个合适的数,或已经找到了所有数独(find=true)。就会返回至dfs(i,j-1),那么其中会有两种情况。
1.如果(i,j-1)位置的为原本就有值的,就会继续返回dfs(i,j-2);
2.如果没有值的话,就会走到if(!find)语句,去判断是舍弃(i,j-1)位置的值去寻找其他的值,还是已经找到结果继续向前返回。
完整代码
class Solution {
//该行是否包含这个数,rows[i][j]代表第i行是否有j+1这个数
boolean[][]rows;
//该列是否包含这个数,columns[i][j]代表第i列是否有j+1这个数
boolean[][]columns;
//这个宫里是否包含这个数tables[i][j]代表第i个宫是否有j+1这个数
boolean[][]tables;
char[][]board;
boolean find = false;
public void solveSudoku(char[][] board) {
this.board = board;
rows = new boolean[9][9];
columns = new boolean[9][9];
tables = new boolean[9][9];
for(int i = 0;i<9;i++)
{
for(int j = 0;j<9;j++)
{
if(board[i][j]!='.')
{
int num = board[i][j]-'0';
rows[i][num-1] = true;
columns[j][num-1] = true;
tables[(i/3)*3+j/3][num-1] = true;
}
}
}
dfs(0,0);
}
//从0,0一直递归到8,8
//一行一行递归,
public void dfs(int i,int j)
{
//到了第10行(也就是说明第9行的第9个已经完成)
if(i==9){
//代表已经找到了结果
find = true;
return ;
}
//之前就不是的空格的数字我们不能改
if(board[i][j]!='.')
{
if(j==8)
//下一行
dfs(i+1,0);
else
//下一列
dfs(i,j+1);
//比如当执行完下一个返回到这里之后,就会执行出循环,返回上一个dfs循环
//假定都在一行,dfs(i,j)为之前就存在的数,那么执行完dfs(i,j+1)后就会返回这里,
//然后程序继续往下走就会跳出循环,然后返回到dfs(i,j-1)中。
}
else{
for(int num=1;num<10;num++)
{
//第i行已经有num,或第j列已经有num
if(rows[i][num-1]||columns[j][num-1])
continue;
int table = (i/3)*3+j/3;
//第table个宫中已经有了num。
if(tables[table][num-1])
continue;
rows[i][num-1] = true;
columns[j][num-1] = true;
tables[table][num-1] = true;
board[i][j] = (char)('0'+num);
if(j==8)
//下一行
dfs(i+1,0);
else
//下一列
dfs(i,j+1);
//这里可能是当前位置不能选取这个数,因为选取完这个数之后下一个位置的数无法找到合适的数
//也可能是当前的i和j下一个位置已经到达终点,然后return,就会走到这里
if(!find){
rows[i][num-1] = false;
columns[j][num-1] = false;
tables[table][num-1] = false;
board[i][j] = '.';
}else{
//如果找到了所有的值,dfs(9,0)就会将find置为true,然后返回dfs(8,8)的if(!find)这里,之后就会继续返回,直到返回dfs(0,0)的这里
return ;
}
}
}
}
}
51. N皇后
题目链接
其实本题最最核心的就是怎么区别主对角和副对角线。主对角线是行-列=常数,副对角线是行+列=常数。

class Solution {
//很明显我们的大体思路为回溯
//接下来要用四个数组来存储哪些位置是不可以走的
//其实可以不要行的判断,因为是一行一行往下走的,不存在该行被选中的问题。
//boolean[]rows;
boolean[]columns;
//其实主对角线和副对角线的判断才是本题的核心
// 主对角线(\)(行-列=常数)
Set<Integer>mains;
// 副对角线(/)(行+列=常数)
Set<Integer>seconds;
//对应每行的j的位置
int[]results;
List<List<String>>list;
int n;
public List<List<String>> solveNQueens(int n) {
list = new ArrayList<>();
this.n = n;
//rows = new boolean[n];
columns = new boolean[n];
mains = new HashSet<>();
seconds = new HashSet<>();
results = new int[n];
dfs(0);
return list;
}
public void dfs(int row)
{
if(row==n)
{
//组成答案
List<String>ll = new ArrayList<>();
for(int i=0;i<n;i++)
{
//一行一行组成
String s = "";
for(int j=0;j<n;j++)
{
if(results[i]==j)
s+="Q";
else
s+=".";
}
ll.add(s);
}
list.add(ll);
return ;
}
for(int j=0;j<n;j++)
{
//该列被占用
if(columns[j])
continue;
int thismain = row-j;
int thissecond = row+j;
//该位置在已经有的主对角线Set里或副对角线Set中。
if(mains.contains(thismain)||seconds.contains(thissecond))
continue;
results[row] = j;
columns[j] = true;
mains.add(thismain);
seconds.add(thissecond);
dfs(row+1);
//走到这里说明row行不可以选用这个j了,
//1.可能是当前列不符合条件(因为row+1行找不到符合的结果)
//2.也可能是包含此列的results已经是一种答案了(在dfs(row+1)时(满足结果直接return;)会返回这里),
//于是接下来要去寻找当前行的其他位置答案。
results[row] = 0;
columns[j] = false;
mains.remove(thismain);
seconds.remove(thissecond);
}
//走出来说明没有一个列是满足当前条件的,就会返回dfs(row)这一行,这一行选取的列不对,要重新选取。
}
}