目标检测框回归损失函数-SmoothL1、Iou、Giou、Diou和Ciou

目录

1 引言

2 检测框回归损失函数

2.1 SmoothL1

     2.1.1 SmoothL1 Torch实现代码

     2.1.2 SmoothL1的缺点

2.2 Iou

      2.2.1 Iou Torch代码实现

      2.2.2 Iou的缺点

2.3 Giou

      2.3.1 Giou Torch实现代码

      2.3.2 Giou 缺点

2.4 Diou和Ciou

     2.4.1 Diou Torch实现代码

     2.4.2 Ciou Torch实现代码 

     2.4.3 Ciou和Diou缺点

3 总结 

 

---

1 引言

    在目标检测的视觉任务中，分类和检测框的回归是核心内容，因此损失函数的选择对模型的表现效果也具有较大影响，对于分类损失函数这里不多做赘述（Focal loss考虑到了正负样本以及难例和简单例平衡的问题，目前已经被各位炼丹师广泛使用。）所以这个博客主要讲解检测框回归损失函数，根据其演变路线SmoothL1>Iou>Giou>Diou>Ciou进行详细介绍。

2 检测框回归损失函数

2.1 SmoothL1

    SmoothL1最早在何凯明大神的Faster RCNN模型中使用到。计算公式如下所示，SmoothL1预测框值和真实框值差的绝对值大于1时采用线性函数，其导数为常数，避免了因差值过大造成梯度爆炸。当差值小于1时采用非线性函数，导数值变小有利用模型收敛到更高精度。

     2.1.1 SmoothL1 Torch实现代码

def Smooth_L1(predict_box,gt_box,th=1.0,reduction = "mean"):
    '''
    predict_box:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
    gt_box:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
    th: float
    reduction:"mean"or"sum"
    return: loss
    '''
    # 计算坐标差
    x_diff = torch.abs(predict_box - gt_box)
    print("x_diff:\n",x_diff)
    #torch.where(fu(ction:: where(condition, x, y) -> Tensor)
    #满足条件返回x，不满足条件返回y
    loss = torch.where(x_diff < th, 0.5 * x_diff * x_diff, x_diff - 0.5)
    print("loss_first_stage:\n",loss)
    if reduction == "mean":
        loss = torch.mean(loss)
    elif reduction == "sum":
        loss = torch.sum(loss)
    else:
        pass
    print("loss_last_stage:\n",loss)
    return loss
if __name__ == "__main__":
    pred_box = torch.tensor([[2,4,6,8],[5,9,13,12]])
    gt_box = torch.tensor([[3,4,7,9]])
    loss = Smooth_L1(predict_box=pred_box,gt_box=gt_box)

#输出结果
"""
x_diff:
 tensor([[1, 0, 1, 1],
        [2, 5, 6, 3]])
loss_first_stage:
 tensor([[0.5000, 0.0000, 0.5000, 0.5000],
        [1.5000, 4.5000, 5.5000, 2.5000]])
loss_last_stage:
 tensor(1.9375)
"""

     2.1.2 SmoothL1的缺点

             在nms或者计算AP的时候对检测框采用的是Iou的标准，因此SmoothL1和评价标准的关联性不是很大，具有相同SmoothL1 值的一对框可能具有不同的Iou。针对这一问题，提出了以下的Iou作为损失函数。

2.2 Iou

       Iou的就是交并比，预测框和真实框相交区域面积和合并区域面积的比值，计算公式如下，Iou作为损失函数的时候只要将其对数值输出就好了。

      2.2.1 Iou Torch代码实现

def Iou_loss(preds, bbox, eps=1e-6, reduction='mean'):
    '''
    preds:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
    bbox:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
    reduction:"mean"or"sum"
    return: loss
    '''
    x1 = torch.max(preds[:, 0], bbox[:, 0])
    y1 = torch.max(preds[:, 1], bbox[:, 1])
    x2 = torch.min(preds[:, 2], bbox[:, 2])
    y2 = torch.min(preds[:, 3], bbox[:, 3])
    
    w = (x2 - x1 + 1.0).clamp(0.)
    h = (y2 - y1 + 1.0).clamp(0.)
    inters = w * h
    print("inters:\n",inters)

    uni = (preds[:, 2] - preds[:, 0] + 1.0) * (preds[:, 3] - preds[:, 1] + 1.0) + (bbox[:, 2] - bbox[:, 0] + 1.0) * (
            bbox[:, 3] - bbox[:, 1] + 1.0) - inters
    print("uni:\n",uni)
    ious = (inters / uni).clamp(min=eps)
    loss = -ious.log()

    if reduction == 'mean':
        loss = torch.mean(loss)
    elif reduction == 'sum':
        loss = torch.sum(loss)
    else:
        raise NotImplementedError
    print("last_loss:\n",loss)
    return loss
if __name__ == "__main__":
    pred_box = torch.tensor([[2,4,6,8],[5,9,13,12]])
    gt_box = torch.tensor([[3,4,7,9]])
    loss = Iou_loss(preds=pred_box,bbox=gt_box)

# 输出结果
"""
inters:
 tensor([20.,  3.])
uni:
 tensor([35., 63.])
last_loss:
 tensor(1.8021)
"""

       2.2.2 Iou的缺点

             当预测框和真实框不相交时Iou值为0，导致很大范围内损失函数没有梯度。针对这一问题，提出了Giou作为损失函数。

2.3 Giou

         Giou Loss先计算闭包区域（闭包区域是包含预测框和检测框的最小区域），再计算闭包区域中不属于两个框区域占闭包区域的比重，最后用Iou减去这个比重。Giou计算公式如下，最后将1-Giou的输出作为损失值。这样也能够衡量出不相交情况下的距离，以及不同相交方式下的距离。论文地址：https://arxiv.org/pdf/1902.09630.pdf

       2.3.1 Giou Torch实现代码

def Giou_loss(preds, bbox, eps=1e-7, reduction='mean'):
    '''
    https://github.com/sfzhang15/ATSS/blob/master/atss_core/modeling/rpn/atss/loss.py#L36
    :param preds:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
    :param bbox:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
    :return: loss
    '''
    ix1 = torch.max(preds[:, 0], bbox[:, 0])
    iy1 = torch.max(preds[:, 1], bbox[:, 1])
    ix2 = torch.min(preds[:, 2], bbox[:, 2])
    iy2 = torch.min(preds[:, 3], bbox[:, 3])

    iw = (ix2 - ix1 + 1.0).clamp(0.)
    ih = (iy2 - iy1 + 1.0).clamp(0.)

    # overlap
    inters = iw * ih
    print("inters:\n",inters)
    # union
    uni = (preds[:, 2] - preds[:, 0] + 1.0) * (preds[:, 3] - preds[:, 1] + 1.0) + (bbox[:, 2] - bbox[:, 0] + 1.0) * (
            bbox[:, 3] - bbox[:, 1] + 1.0) - inters + eps
    print("uni:\n",uni)
    # ious
    ious = inters / uni
    print("Iou:\n",ious)
    ex1 = torch.min(preds[:, 0], bbox[:, 0])
    ey1 = torch.min(preds[:, 1], bbox[:, 1])
    ex2 = torch.max(preds[:, 2], bbox[:, 2])
    ey2 = torch.max(preds[:, 3], bbox[:, 3])
    ew = (ex2 - ex1 + 1.0).clamp(min=0.)
    eh = (ey2 - ey1 + 1.0).clamp(min=0.)

    # enclose erea
    enclose = ew * eh + eps
    print("enclose:\n",enclose)

    giou = ious - (enclose - uni) / enclose
    loss = 1 - giou

    if reduction == 'mean':
        loss = torch.mean(loss)
    elif reduction == 'sum':
        loss = torch.sum(loss)
    else:
        raise NotImplementedError
    print("last_loss:\n",loss)
    return loss
if __name__ == "__main__":
    pred_box = torch.tensor([[2,4,6,8],[5,9,13,12]])
    gt_box = torch.tensor([[3,4,7,9]])
    loss = Giou_loss(preds=pred_box,bbox=gt_box)

# 输出结果
"""
inters:
 tensor([20.,  3.])
uni:
 tensor([35., 63.])
Iou:
 tensor([0.5714, 0.0476])
enclose:
 tensor([36., 99.])
last_loss:
 tensor(0.8862)
"""

      2.3.2 Giou 缺点

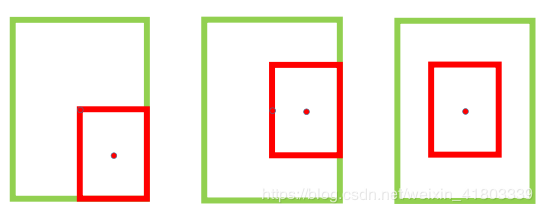
              如下图所示，当预测框被真实框包含，或者真实框被预测框包含，则闭包区域和相并区域一样，因此Giou退化为Iou，未能反映出包含的各种方式，针对这一问题，提出了Diou和Ciou。

2.4 Diou和Ciou

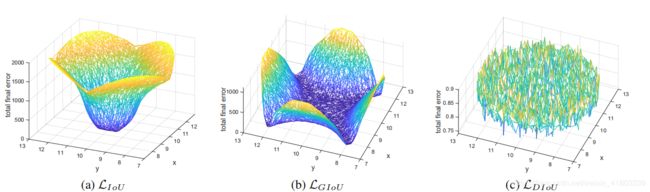
       Diou和Ciou是哥哥和弟弟的关系，是在同一篇论文中被提出。论文链接：https://arxiv.org/pdf/1911.08287.pdf，在论文中作者对Iou和Giou进行对比：(1)认为Iou和Giou收敛速度较慢，因此需要更多的迭代步数。（2）特殊情况下（互相包含），Iou和Giou错误率依旧很高，如下图所示：

    论文的贡献点总结为四点：

     （1）Diou相对Giou效率高，模型更易收敛。

     （2）Ciou对精度更加有利，考虑到了三个重要的几何因素：重叠面积、中心点距离和长宽比。能够更好的描述框的回归问题。

     （3）Diou能够直接插入到后处理过程nms里面，比原始nms里面用到的Iou表现更好。

     （4）Diou和Ciou的可移植性强，很牛逼！

    Diou计算公式如下：

    式中：b和b(gt)分别表示预测框和真实框的中心点，然后计算欧式距离的平方。c表示预测框和真实框的最小闭包区域的对角线长度。

     2.4.1 Diou Torch实现代码

def Diou_loss(preds, bbox, eps=1e-7, reduction='mean'):
    '''
    preds:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
    bbox:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
    eps: eps to avoid divide 0
    reduction: mean or sum
    return: diou-loss
    '''
    ix1 = torch.max(preds[:, 0], bbox[:, 0])
    iy1 = torch.max(preds[:, 1], bbox[:, 1])
    ix2 = torch.min(preds[:, 2], bbox[:, 2])
    iy2 = torch.min(preds[:, 3], bbox[:, 3])

    iw = (ix2 - ix1 + 1.0).clamp(min=0.)
    ih = (iy2 - iy1 + 1.0).clamp(min=0.)

    # overlaps
    inters = iw * ih

    # union
    uni = (preds[:, 2] - preds[:, 0] + 1.0) * (preds[:, 3] - preds[:, 1] + 1.0) + (bbox[:, 2] - bbox[:, 0] + 1.0) * (
            bbox[:, 3] - bbox[:, 1] + 1.0) - inters

    # iou
    iou = inters / (uni + eps)
    print("iou:\n",iou)

    # inter_diag
    cxpreds = (preds[:, 2] + preds[:, 0]) / 2
    cypreds = (preds[:, 3] + preds[:, 1]) / 2

    cxbbox = (bbox[:, 2] + bbox[:, 0]) / 2
    cybbox = (bbox[:, 3] + bbox[:, 1]) / 2

    inter_diag = (cxbbox - cxpreds) ** 2 + (cybbox - cypreds) ** 2
    print("inter_diag:\n",inter_diag)

    # outer_diag
    ox1 = torch.min(preds[:, 0], bbox[:, 0])
    oy1 = torch.min(preds[:, 1], bbox[:, 1])
    ox2 = torch.max(preds[:, 2], bbox[:, 2])
    oy2 = torch.max(preds[:, 3], bbox[:, 3])

    outer_diag = (ox1 - ox2) ** 2 + (oy1 - oy2) ** 2
    print("outer_diag:\n",outer_diag)

    diou = iou - inter_diag / outer_diag
    diou = torch.clamp(diou, min=-1.0, max=1.0)

    diou_loss = 1 - diou
    print("last_loss:\n",diou_loss)

    if reduction == 'mean':
        loss = torch.mean(diou_loss)
    elif reduction == 'sum':
        loss = torch.sum(diou_loss)
    else:
        raise NotImplementedError
    return loss
if __name__ == "__main__":
    pred_box = torch.tensor([[2,4,6,8],[5,9,13,12]])
    gt_box = torch.tensor([[3,4,7,9]])
    loss = Diou_loss(preds=pred_box,bbox=gt_box)

# 输出结果
"""
iou:
 tensor([0.5714, 0.0476])
inter_diag:
 tensor([ 1, 32])
outer_diag:
 tensor([ 50, 164])
last_loss:
 tensor([0.4286, 0.9524])
"""

      Ciou在Diou的基础上进行改进，认为Diou只考虑了中心点距离和重叠面积，但是没有考虑到长宽比。

      Ciou计算公式： 

      2.4.2 Ciou Torch实现代码 

import math
def Ciou_loss(preds, bbox, eps=1e-7, reduction='mean'):
    '''
    https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/loss/multibox_loss.py
    :param preds:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
    :param bbox:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
    :param eps: eps to avoid divide 0
    :param reduction: mean or sum
    :return: diou-loss
    '''
    ix1 = torch.max(preds[:, 0], bbox[:, 0])
    iy1 = torch.max(preds[:, 1], bbox[:, 1])
    ix2 = torch.min(preds[:, 2], bbox[:, 2])
    iy2 = torch.min(preds[:, 3], bbox[:, 3])

    iw = (ix2 - ix1 + 1.0).clamp(min=0.)
    ih = (iy2 - iy1 + 1.0).clamp(min=0.)

    # overlaps
    inters = iw * ih

    # union
    uni = (preds[:, 2] - preds[:, 0] + 1.0) * (preds[:, 3] - preds[:, 1] + 1.0) + (bbox[:, 2] - bbox[:, 0] + 1.0) * (
            bbox[:, 3] - bbox[:, 1] + 1.0) - inters

    # iou
    iou = inters / (uni + eps)
    print("iou:\n",iou)

    # inter_diag
    cxpreds = (preds[:, 2] + preds[:, 0]) / 2
    cypreds = (preds[:, 3] + preds[:, 1]) / 2

    cxbbox = (bbox[:, 2] + bbox[:, 0]) / 2
    cybbox = (bbox[:, 3] + bbox[:, 1]) / 2

    inter_diag = (cxbbox - cxpreds) ** 2 + (cybbox - cypreds) ** 2

    # outer_diag
    ox1 = torch.min(preds[:, 0], bbox[:, 0])
    oy1 = torch.min(preds[:, 1], bbox[:, 1])
    ox2 = torch.max(preds[:, 2], bbox[:, 2])
    oy2 = torch.max(preds[:, 3], bbox[:, 3])

    outer_diag = (ox1 - ox2) ** 2 + (oy1 - oy2) ** 2

    diou = iou - inter_diag / outer_diag
    print("diou:\n",diou)

    # calculate v,alpha
    wbbox = bbox[:, 2] - bbox[:, 0] + 1.0
    hbbox = bbox[:, 3] - bbox[:, 1] + 1.0
    wpreds = preds[:, 2] - preds[:, 0] + 1.0
    hpreds = preds[:, 3] - preds[:, 1] + 1.0
    v = torch.pow((torch.atan(wbbox / hbbox) - torch.atan(wpreds / hpreds)), 2) * (4 / (math.pi ** 2))
    alpha = v / (1 - iou + v)
    ciou = diou - alpha * v
    ciou = torch.clamp(ciou, min=-1.0, max=1.0)

    ciou_loss = 1 - ciou
    if reduction == 'mean':
        loss = torch.mean(ciou_loss)
    elif reduction == 'sum':
        loss = torch.sum(ciou_loss)
    else:
        raise NotImplementedError
    print("last_loss:\n",loss)
    return loss
if __name__ == "__main__":
    pred_box = torch.tensor([[2,4,6,8],[5,9,13,12]])
    gt_box = torch.tensor([[3,4,7,9]])
    loss = Ciou_loss(preds=pred_box,bbox=gt_box)

# 输出结果
"""
iou:
 tensor([0.5714, 0.0476])
diou:
 tensor([0.5714, 0.0476])
last_loss:
 tensor(0.6940)
"""

     2.4.3 Ciou和Diou缺点

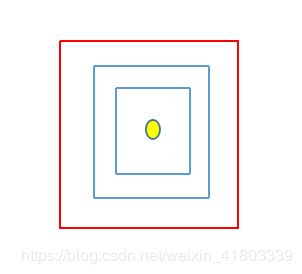
             通过对论文的理解，我认为Ciou和Diou依然有一些特殊情况没有解决。如下图所示，红色代表真实框，蓝色表示预测框，当共中心点时，Diou退化为Iou，当然Ciou因为长宽比惩罚项的原因能对这一情况有很好的处理，但是当出现共中心点、预测框和真实框的长宽比也相同的情况则Ciou也退化为Iou。因为我认为应该从Ciou的alpha*v的惩罚项入手，设计新的惩罚项来避免这种情况，我愿意将未来的这种检测框回归损失函数称为Yiyi_Iou。

3 总结 

      希望我的这篇文章能对你产生帮助。