【Python - OpenCV】数字图像项目实战（二） - 数字图像处理算法基础

1.理论架构

基础知识汇总篇：
https://blog.csdn.net/weixin_42237113/article/details/104500993
API详解：
https://blog.csdn.net/weixin_42237113/article/details/104488809

2.基础梗概

2.1卷积滤波

1.1卷积滤波基本原理：

线性滤波可以说是图像处理最基本的方法，它可以允许我们对图像进行处理，产生很多不同的效果。做法很简单。首先，我们有一个二维的滤波器矩阵（有个高大上的名字叫卷积核）和一个要处理的二维图像。然后，对于图像的每一个像素点，计算它的邻域像素和滤波器矩阵的对应元素的乘积，然后加起来，作为该像素位置的值。这样就完成了滤波过程。

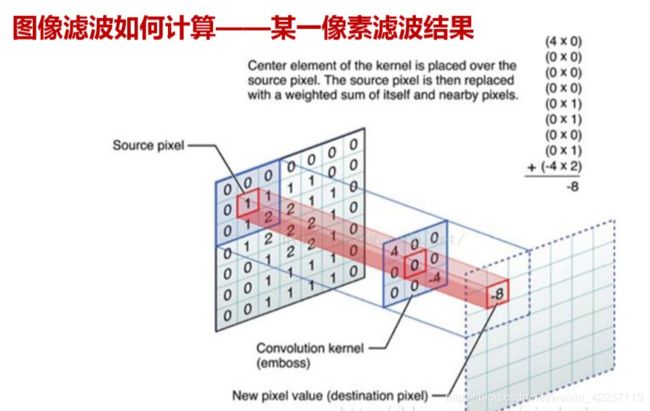
对图像和滤波矩阵进行逐个元素相乘再求和的操作就相当于将一个二维的函数移动到另一个二维函数的所有位置，这个操作就叫卷积或者协相关。卷积和协相关的差别是，卷积需要先对滤波矩阵进行180的翻转，但如果矩阵是对称的，那么两者就没有什么差别了。

ref:
https://blog.csdn.net/zouxy09/article/details/49080029
https://www.jianshu.com/p/8dfe02b61686

2.2 图像平滑滤波算法

常见平滑滤波算法：
均值滤波、高斯滤波、中值滤波

均值滤波：

从待处理图像首元素开始用模板对原始图像进行卷积，均值滤波直观地理解就是用相邻元素灰度值的平均值代替该元素的灰度值。
在一个小区域内（通常3*3）像素值平均,表示为：

高斯滤波：

高斯滤波一般针对的是高斯噪声，能够很好的抑制图像输入时随机引入的噪声，将像素点跟邻域像素看作是一种高斯分布的关系，它的操作是将图像和一个高斯核进行卷积操作。
模板：通过高斯内核函数产生的高斯内核函数：

中值滤波：

同样是空间域的滤波，主题思想是取相邻像素的点，然后对相邻像素的点进行排序，取中点的灰度值作为该像素点的灰度值。
统计排序滤波器，对椒盐噪声有很好的抑制

ref:https://blog.csdn.net/csdnforyou/article/details/82216301

2.3 边缘检测的基本原理（Sobel、LoG和Canny算子的原理说明、及其差异）。

边缘检测基本原理

先来看张图，左边是原图，右边是边缘检测后的图，边缘检测就是检测出图像上的边缘信息，右图用白色的程度表示边缘的深浅。

边缘其实就是图像上灰度级变化很快的点的集合。

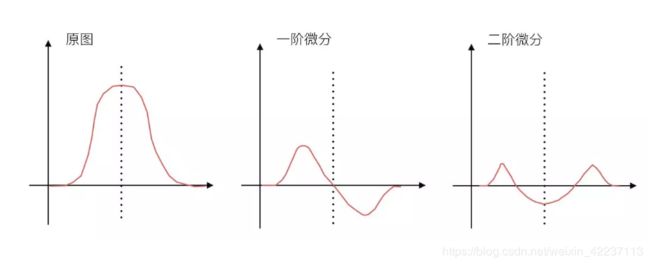
如上图所示，图像的灰度值、灰度值一阶导数、二阶导数在边缘点的变化，都有共同特点：

	（1）一阶导数在边缘点正好是极值点（最大、最小值）
	（2）二阶导数在边缘点为0。因此检测边缘即使检测相关图像的微分值变化过程。实际中计算x,y方向差分来计算。

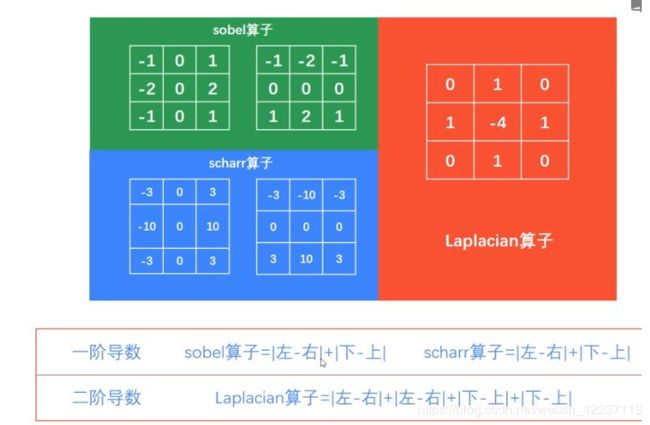
sobel/log/canny算子的原理差异

sobel算子
（以3*3为例）如下所示：

sobel算子边缘算子所采用的算法是先进行加权平均，然后进行微分运算，算子的计算方法如上。
Sobel算子垂直方向和水平方向的模板如图中相关模板的第一、二个矩阵，前者可以检测出图像中的水平方向的边缘，后者则可以检测图像中垂直方向的边缘。图像的每一个像素的横向及纵向梯度近似值的平方和，来计算梯度的大小。
sobel算子不但产生较好的检测效果，而且对噪声具有平滑抑制作用，但是得到的边缘较粗，且可能出现伪边缘。

LoG算子
先对图象平滑，后拉氏变换求二阶微分，等效于把拉氏变化作用于平滑函数，得到1个兼有平滑和二阶微分作用的模板，再与原来的图像进行卷积。用Marr-Hildreth模板与图像进行卷积的优点在于，模板可以预先算出，实际计算可以只进行卷积。

LOG滤波器有以下特点:
(1)通过图象平滑，消除了一切尺度小于σ的图像强度变化;
(2)若用其它微分法，需要计算不同方向的微分，而它无方向性，因此可以节省计算量;
(3)它定位精度高，边缘连续性好，可以提取对比度较弱的边缘点。
LOG滤波器也有它的缺点:当边缘的宽度小于算子宽度时，由于过零点的斜坡融合将会丢失细节。
LOG滤波器有无限长的拖尾，若取得很大尺寸，将使得计算不堪重负。

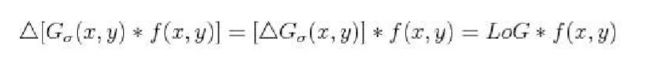
Canny算子
Canny算子是是一阶算子。
其方法的实质是用1个准高斯函数作平滑运算fs=f(x,y)*G(x,y),
然后以带方向的一阶微分算子定位导数最大值。
Canny算子也可用高斯函数的梯度来近似，在理论上很接近4个指数函数的线性组合形成的最佳边缘算子。在实际工作应用中编程较为复杂且运算较慢。

ref: https://www.jianshu.com/p/2334bee37de5
https://blog.csdn.net/aidem_brown/article/details/81542996

3. 直方图和大津算法（ostu）

3.1 直方图基本概念

• 统计各个灰度级别在图像中的出现次数或概率，并用直方图显示出来，一般直方图显示图像数据时会以左暗又亮的分布曲线形式呈现出来。
• 图像直方图由于其计算代价较小，且具有图像平移、旋转、缩放不变性等众多优点，广泛地应用于图像处理的各个领域，特别是灰度图像的阈值分割、基于颜色的图像检索以及图像分类。

3.2 大津算法进行图像分割的基本原理

基本原理

• 在计算机视觉和图像处理中，大津二值化法用来自动对基于聚类的图像进行二值化，或者说，将一个灰度图像退化为二值图像。算法假定该图像根据双模直方图（前景像素和背景像素）把包含两类像素，于是它要计算能将两类分开的最佳阈值，使得它们的类内方差最小；由于两两平方距离恒定，所以即它们的类间方差最大。因此，大津二值化法粗略的来说就是一维Fisher判别分析的离散化模拟。

计算过程

• 遍历灰度取值，确定最佳阈值，使背景和目标之间的类间方差最大 (因为二者差异最大)；
• （1）记t为前景与背景的分割阈值，前景点数占图像比例为w0，平均灰度为u0；背景点数占图像比例为w1，平均灰度为u1。则图像的总平均灰度为：u=w0u0+w1u1。
• （2）前景和背景图象的方差：g=w0*(u0-u)(u0-u)+w1(u1-u)(u1-u)=w0w1*(u0-u1)*(u0-u1),此公式为方差公式。
• （3）当方差g最大时，可以认为此时前景和背景差异最大，此时的灰度t是最佳阈值sb = w0w1(u1-u0)*(u0-u1)

4. Harris角点检测

ref : https://blog.csdn.net/zhyh1435589631/article/details/62039743

4.1 Harris算子对角点定义
Harris算子是Harris和Stephens在1998年提出的一种基于信号的点特征提取算子。其前身是Moravec算子。

4.2 对角点检测基本原理

基本现象：

• 在灰度变化平缓区域，窗口内像素灰度积分近似保持不变
• 在边缘区域，边缘方向：灰度积分近似不变，其余任意方向 ：剧烈变化；
• 在角点处，任意方向均剧烈变化
  
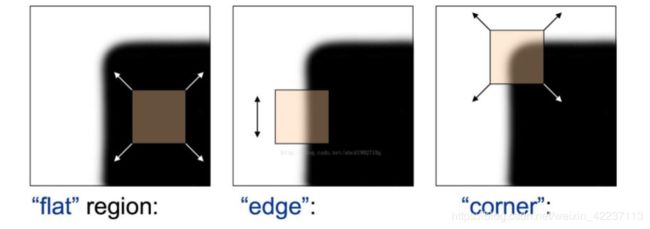
  可以通过灰度积分的变化情况不同，检测出相关的角点。

对于图像I(x,y)，当在点(x,y)处平移(Δx,Δy)后的自相似性，可以通过自相关函数给出：

   c(x,y;Δx,Δy)=   ∑    w(u,v)(I(u,v)–I(u+Δx,v+Δy))2
            (u,v)∈W(x,y)

其中，W(x,y)是以点(x,y)为中心的窗口，w(u,v)为加权函数，它既可是常数，也可以是高斯加权函数。

根据泰勒展开，对图像I(x,y)在平移(Δx,Δy)后进行一阶近似：

I(u+Δx,v+Δy)=I(u,v)+Ix(u,v)Δx+Iy(u,v)Δy+O(Δx2,Δy2)
         ≈I(u,v)+Ix(u,v)Δx+Iy(u,v)Δy

其中，Ix,Iy是图像I(x,y)的偏导数，这样的话，自相关函数则可以简化为：

c(x,y;Δx,Δy)≈∑w(Ix(u,v)Δx+Iy(u,v)Δy)^ 2=[Δx,Δy]M(x,y)[ΔxΔy]

其中

    M(x,y)=∑w[ Ix(x,y)^2       Ix(x,y)Iy(x,y)
            Ix(x,y)Iy(x,y)     Iy(x,y)2     ]     =
    
    [∑wIx(x,y)^2         ∑wIx(x,y)Iy(x,y)
    ∑wIx(x,y)Iy(x,y)      ∑wIy(x,y)^2        ]
    
    =[ A C
      C B]

也就是说图像I(x,y)在点(x,y)处平移(Δx,Δy)后的自相关函数可以近似为二项函数：

c(x,y;Δx,Δy)≈AΔx^2+2CΔxΔy+BΔy^2

其中

A=∑wIx^2,
B=∑wIy^2,
C=∑wIxIy

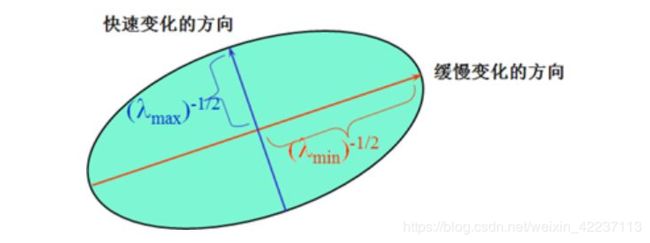
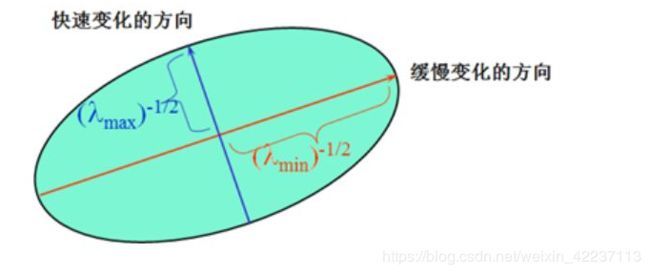
二次项函数本质上就是一个椭圆函数。椭圆的扁率和尺寸是由M(x,y)的特征值λ1、λ2决定的，椭贺的方向是由M(x,y)的特征矢量决定的，如下图所示，椭圆方程为：

    [Δx,Δy]M(x,y)[Δx  = 1
               	  Δy]

椭圆函数特征值与图像中的角点、直线（边缘）和平面之间的关系如下图所示。共可分为三种情况：

• 图像中的直线一个特征值大，另一个特征值小，λ1≫λ2或λ2≫λ1。自相关函数值在某一方向上大，在其他方向上小。
• 图像中的平面。两个特征值都小，且近似相等；自相关函数数值在各个方向上都小。
• 图像中的角点。两个特征值都大，且近似相等，自相关函数在所有方向都增大
  。

4.3 引入对角点相应函数的意义

根据二次项函数特征值的计算公式，我们可以求M(x,y)矩阵的特征值。但是Harris给出的角点差别方法并不需要计算具体的特征值，而是计算一个角点响应值R来判断角点。R的计算公式为：

R=detM−α(traceM)2   

detM=λ1λ2 = AC−B^2 ,  
 
traceM=λ2+λ2 = A + C

式中，detM为矩阵的行列式；traceM为矩阵M的直迹；α为经常常数，取值范围为0.04~0.06。M如下

        M=[A   B   
           B   C]

• 当R接近于零时，处于灰度变化平缓区域；
• 当R<0时，点为边界像素；
• 当R>0时，点为角点。

引入角点响应函数的意义是由于λ1、λ2的大小是相对而言的，无法量化进行判断，所以引入角点响应函数，方便判断该点是否是角点。

5. Hough变换的基本原理(包括参数空间变换及参数空间划分网格统计)。

5.1 Hough变换的基本原理

参数空间变化：
霍夫变换最简单的是检测直线。我们知道，直线的方程表示可以由斜率和截距表示（这种表示方法，称为斜截式），如下所示：

    y= mx + b   (1)

如果用参数空间表示则为(b,m),即用斜率和截距就能表示一条直线。
  但是这样会参数问题，垂直线的斜率不存在（或无限大），这使得斜率参数m的值接近于无限。为此，为了更好的计算，Richard O. Duda和Peter E. Hart在1971年4月，提出了Hesse normal form(Hesse法线式).

	r=xcosθ+ysinθ  (2)

其中r是原点到直线上最近点的距离(其他人可能把这记录为ρ，下面也可以把r看成参数ρ)，θ是x轴与连接原点和最近点直线之间的夹角。如图所示。

直角坐标系的一点(x,y)，对应极坐标系下 的一条正弦曲线.同一条直线上的多个点，在极坐标系下必 相交于一点。通过在参数空间中的多条正弦曲线的角点，可以找到此时的极坐标，从而可以反推出相关直线的坐标公式。
因此，可以将图像的每一条直线与一对参数(r,θ)相关联,这个参数(r,θ)平面有时被称为霍夫空间，用于二维直线的集合。

网格统计：
将空间量化成许多小格 ，根据x-y平面每一个直线点代入θ的量化值 ，算出各个ρ，将对应格计数累加。 当全部点变换后，对小格进行检验。设置累计阈值T，计数器大于T的小格对应于共 线点，其可以用作直线拟合参数。小于T 的反映非共线点，丢弃不用。

6. SIFT、ORB算子原理。

SIFT原理

SIFT，即尺度不变特征变换（Scale-invariant feature transform，SIFT），是用于图像处理领域的一种描述。这种描述具有尺度不变性，可在图像中检测出关键点，是一种局部特征描述子。
尺度空间理论的基本思想是：在图像信息处理模型中引入一个被视为尺度的参数，通过连续变化尺度参数获得多尺度下的尺度空间表示序列，对这些序列进行尺度空间主轮廓的提取，并以该主轮廓作为一种特征向量，实现边缘、角点检测和不同分辨率上的特征提取等。
方向直方图原理：为了使描述符具有旋转不变性，需要利用图像的局部特征为给每一个关键点分配一个基准方向。使用图像梯度的方法求取局部结构的稳定方向。对于在DOG金字塔中检测出的关键点点，采集其所在高斯金字塔图像3σ邻域窗口内像素的梯度和方向分布特征。

ORB算子原理

ORB采用FAST（features from accelerated segment test）算法来检测特征点。FAST核心思想就是找出那些卓尔不群的点，即拿一个点跟它周围的点比较，如果它和其中大部分的点都不一样就可以认为它是一个特征点。

1.FAST具体计算过程：

从图片中选取一个像素点P，下面我们将判断它是否是一个特征点。我们首先把它的密度（即灰度值）设为Ip。
设定一个合适的阙值t ：当2个点的灰度值之差的绝对值大于t时，我们认为这2个点不相同。
考虑该像素点周围的16个像素。

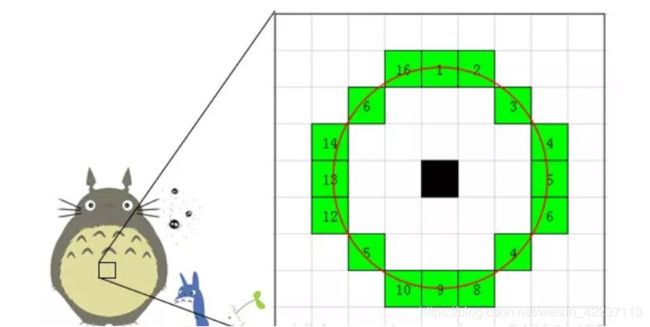
现在如果这16个点中有连续的n个点都和点不同，那么它就是一个角点。 这里n设定为12。
我们现在提出一个高效的测试，来快速排除一大部分非特征点的点。该测试仅仅检查在位置1、9、5和13四个位置的像素（首先检查1和9，看它们是否和点相同。如果是，再检查5和13）。如果是一个角点，那么上述四个像素点中至少有3个应该和点相同。如果都不满足，那么不可能是一个角点。

2.BRIEF： 

得到特征点后我们需要以某种方式F描述这些特征点的属性。这些属性的输出我们称之为该特征点的描述子（Feature DescritorS）.ORB采用BRIEF算法来计算一个特征点的描述子。BRIEF算法的核心思想是在关键点P的周围以一定模式选取N个点对，把这N个点对的比较结果组合起来作为描述子。 具体来讲分为以下几步。

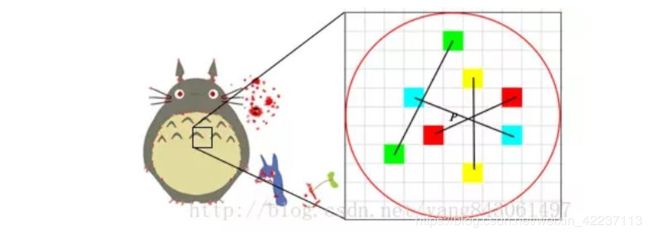
1.以关键点P为圆心，以d为半径做圆O。
2.在圆O内某一模式选取N个点对。这里为方便说明，N=4，实际应用中N可以取512.
假设当前选取的4个点对如上图所示分别标记为：
P1(A,B)、P2(A,B)、P3(A,B)、P4(A,B)

3.定义操作T

4.分别对已选取的点对进行T操作，将得到的结果进行组合。
假如：

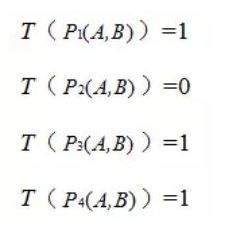
则最终的描述子为：1011

3.代码实践

1. 以Lena为原始图像，通过OpenCV实现平均滤波，高斯滤波及中值滤波，比较滤波结果。

# Q1.图片低通滤波
import cv2
from matplotlib import pyplot as plt

img_ori = cv2.imread("./lena.jpg")
img = cv2.resize(img, (int(img_ori.shape[1]/2), int(img_ori.shape[0]/2)))

# 均值
img_average = cv2.blur(img, (5,5))

# 高斯
img_gaussian = cv2.GaussianBlur(img, (5,5), 0)

# 中值
img_midia = cv2.medianBlur(img, 5)

cv2.imshow("original", img)
cv2.imshow("average", img_average)
cv2.imshow("gaussian", img_gaussian)
cv2.imshow("median", img_midia)

cv2.waitKey()
cv2.destroyAllWindows()

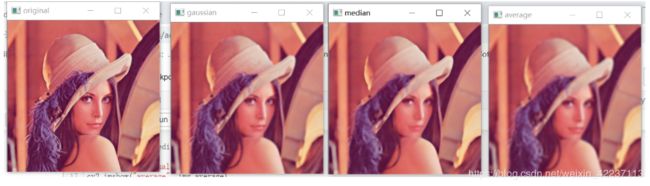
从上图的可以看到，滤波后清晰度，guassian > median > average；
但是如果有椒盐噪声的话，median会是最好

2. 以Lena为原始图像，通过OpenCV使用Sobel及Canny算子检测，比较边缘检测结果。
   sobel/scharr/laplacian算子差异：
   

#Q2.边缘检测
import cv2

# 滤波、变灰度和直接读取灰度图片作用一样
# img_org = cv2.imread("./lena.jpg")
# img_gauss = cv2.GaussianBlur(img_org, (3,3), 0)
# img_size = cv2.resize(img_gauss,(int(img_gauss.shape[0]*0.5),int(img_gauss.shape[1]*0.6)))
# img = cv2.cvtColor(img_size, cv2.COLOR_BGR2GRAY)

# 直接读取灰度图片
img_org = cv2.imread("./lena.jpg",cv2.IMREAD_GRAYSCALE)
img = cv2.resize(img_org,(int(img_org.shape[0]*0.5),int(img_org.shape[1]*0.6)))

# sobel 边缘检测
sobelx = cv2.Sobel(img,cv2.CV_64F,1,0)
sobely = cv2.Sobel(img,cv2.CV_64F,0,1)
sobelx_abs = cv2.convertScaleAbs(sobelx) #转回uint8
sobely_abs = cv2.convertScaleAbs(sobely)
sobelxy = cv2.addWeighted(sobelx,0.5,sobely,0.5,0)

# sobel wrong
sobel_xy = cv2.Sobel(img, -1, 1, 1)

# scharr 边缘检测
scharrx = cv2.Scharr(img,cv2.CV_64F,1,0)
scharry = cv2.Scharr(img,cv2.CV_64F,0,1)
scharrx_abs = cv2.convertScaleAbs(scharrx)
scharry_abs = cv2.convertScaleAbs(scharry)
scharrxy = cv2.addWeighted(scharrx,0.5,scharry,0.5,0)

# laplacian算子
laplacian = cv2.Laplacian(img, cv2.CV_64F)
la_abs = cv2.convertScaleAbs(laplacian)

# Cannny算子
# canny = cv2.Canny(img, 100, 200)#大阈值
# canny = cv2.Canny(img, 50, 60)#小阈值
canny = cv2.Canny(img, 50, 120)

cv2.imshow("original",img)
cv2.imshow("Sobel",sobelxy)
cv2.imshow("Sobel_wrong", sobel_xy)
# sobel_x -> 让图片信息丢失，只保留x轴信息（我觉得课上演示有问题，按照此处理方法）
cv2.imshow("soble_x",cv2.Sobel(img,-1,1,0))
cv2.imshow("Scharr",scharrxy)
cv2.imshow("Laplacian", la_abs)
cv2.imshow("Canny",canny)

cv2.waitKey()
cv2.destroyAllWindows()

比较经过滤波+ cvtcolor转换 和直接读取灰度图片，最终结果图片区别不大。可能因为图片中明显噪点不多、滤波影响较小。
(1)sobel 算子：
如果ddepth = -1(保持原图。但是遇到 白->黑边界点，计算值为负数，会被溢出强制保留为0。所以此类边界会丢失），并且dx=1;dy=1，同时保留x,y轴信息的情况下，图像出现比较虚的现象，很多信息丢失。 如果ddepth = -1, 并且只保留x轴信息的话，图像较为暗淡，过度不明显，像是凸像画。 如果选择避免溢出、通过权重方式合成x,y轴信息，图像检测边界点过于细碎。
(2) Laplacian算子：
图像边界虚化严重，“毛边”严重
(3) canny算子：
边界化情况相对较好，只勾勒了一些边界内容。

3. 在OpenCV安装目录下找到课程对应演示图片(安装目录\sources\samples\data)，首先计算灰度直方图，进一步使用大津算法进行分割，并比较分析分割结果。

# Q3 直方图
import cv2
import matplotlib.pyplot as plt

# 直方图
img = cv2.imread("./lena.jpg")
cv2.imshow("original",img)

# matplot直方图
img_plt = plt.hist(img.ravel(), 256, [0, 255])
plt.xlabel("scores")
plt.ylabel("counts")
plt.show()

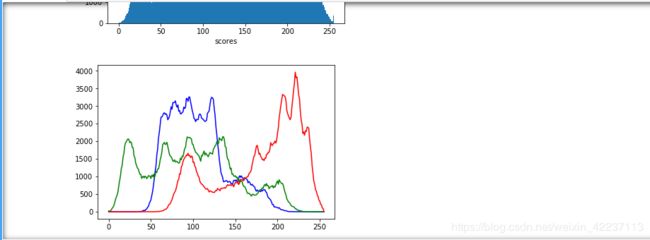
# opencv直方图
img_b = cv2.calcHist([img],[0],None,[256],[0,255])
img_g = cv2.calcHist([img],[1],None,[256],[0,255])
img_r = cv2.calcHist([img],[2],None,[256],[0,255])
plt.plot(img_b,color='b')
plt.plot(img_g,color='g')
plt.plot(img_r,color='r')
plt.show()

cv2.waitKey()
cv2.destroyAllWindows()

# Q3 大津算法分割
import cv2
import matplotlib.pyplot as plt

img_org = cv2.imread("./rice.jpg")#读取图片
# img_org = cv2.resize(img_org, (int(img_org.shape[0]/2),int(img_org.shape[1]/2)))

# img_blur = cv2.GaussianBlur(img_org, (5,5), 0) # 高斯滤波
img_blur = cv2.medianBlur(img_org, 5) # 椒盐噪声，选择中值滤波
img = cv2.cvtColor(img_blur, cv2.COLOR_BGR2GRAY) # 灰度变换

# ostu's阈值
ret,th = cv2.threshold(img, 0, 255, cv2.THRESH_OTSU)
element = cv2.getStructuringElement(cv2.MORPH_CROSS,(3, 3)) #形态学去噪
dst=cv2.morphologyEx(th,cv2.MORPH_OPEN,element)  #开运算去噪

# 自适应阈值：均值效果优于高斯；高斯会引入较多噪点，尤其当block size较小
# dst = cv2.adaptiveThreshold(img,255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY,103, 1) #自适应阈值法，阈值取平均值
dst = cv2.adaptiveThreshold(img,255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY,103, 1) #阈值取高斯函数权重分布
element = cv2.getStructuringElement(cv2.MORPH_CROSS,(3, 3))#形态学去噪
dst=cv2.morphologyEx(dst,cv2.MORPH_OPEN,element)  #开运算去噪

cv2.imshow("original", img_org)
cv2.imshow("ostu_global",th)
cv2.imshow("adapt",dst)

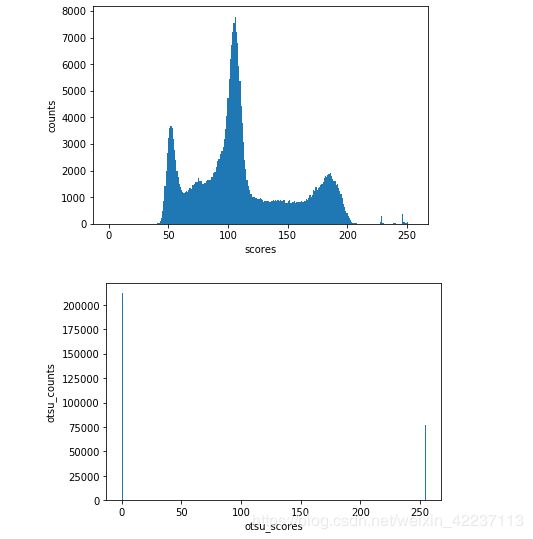
img_plt = plt.hist(img.ravel(), 256, [0, 255])
plt.xlabel("scores")
plt.ylabel("counts")
plt.show()

img_plt = plt.hist(th.ravel(), 256, [0, 255])
plt.xlabel("otsu_scores")
plt.ylabel("otsu_counts")
plt.show()

cv2.waitKey()
cv2.destroyAllWindows()

4. 使用米粒图像，分割得到各米粒，首先计算各区域(米粒)的面积、长度等信息，进一步计算面积、长度的均值及方差，分析落在3sigma范围内米粒的数量。

# Q4 米粒检测问题

import cv2
import copy
import numpy as np


img = cv2.imread("./rice.jpg")
grey = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) #转换为灰度图
cv2.imshow("original image", img)
cv2.imshow("grey", grey)

dst = cv2.adaptiveThreshold(grey, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY,103, 1) #阈值取高斯函数权重分布
element = cv2.getStructuringElement(cv2.MORPH_CROSS,(3, 3))#形态学去噪
bw = cv2.morphologyEx(dst,cv2.MORPH_OPEN,element)  #开运算去噪

seg = copy.deepcopy(bw)
bin, cnts, hier = cv2.findContours(seg, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE) # 检测米粒轮廓

# 分析目标
count = 0
area_array = np.array([])  # 米粒面积数组
line_array = np.array([])  # 米粒长度数组

for i in range(len(cnts), 0, -1):
    cnt = cnts[i - 1]
    area = cv2.contourArea(cnt)  # 计算米粒面积
    if area < 10:
        continue
#     if area < 10 or area > 1700:
#         continue
    count = count + 1
    area_array = np.append(area_array, area)

    minAreaRect = cv2.minAreaRect(cnt) # 精确米粒边界
    x, y, z, p = cv2.boxPoints(minAreaRect)  # 得到米粒的4个坐标
    
    # 计算米粒的长度
    l1 = ((x[0] - y[0]) ** 2 + (x[1] - y[1]) ** 2) ** 0.5 # 第一个点和第二个点的欧几里得距离，相当于矩阵长度
    l2 = ((x[0] - p[0]) ** 2 + (x[1] - p[1]) ** 2) ** 0.5 # 第一个点和第四个点的欧几里得距离，相当于矩阵宽度
    if l1 > l2:
        line = l1
    else:
        line = l2
    print("米粒", i, "面积:", area, "长度:", round(line, 2))
    line_array = np.append(line_array, line)
    cv2.line(img, tuple(x), tuple(y), (255, 0, 0), 1)
    cv2.line(img, tuple(y), tuple(z), (255, 0, 0), 1)
    cv2.line(img, tuple(z), tuple(p), (255, 0, 0), 1)
    cv2.line(img, tuple(p), tuple(x), (255, 0, 0), 1)
    cv2.putText(img, str(count), (x[0], x[1]), cv2.FONT_HERSHEY_PLAIN, 0.5, (0, 0xff, 0)) # 标记字体信息

print("------------------------------")

print("米粒总数量: ", len(area_array))
print("------------------------------")

area_all = area_array.sum()
print("总面积:", round(area_all, 3))
average_area = area_all / count
print("平均面积:", round(average_area, 3))
std = area_array.std()
print("面积标准差:", round(std, 3))
area1 = average_area - std * 3
area2 = average_area + std * 3
# 3 sigma原理：https://zhidao.baidu.com/question/585044313.html
print("面积3sigma的取值范围:", round(area1, 3), "--", round(area2, 3))
count1 = 0
for i in area_array:
    if i > area1 and i < area2:
        count1 = count1 + 1
print("米粒面积在3sigma内的数量为:", count1)

print("------------------------------")

line_all = line_array.sum()
print("总长度:", round(line_all, 3))
average_line = line_all / count
print("平均长度:", round(average_line, 3))
std_line = line_array.std()
print("长度标准差:", round(std_line, 3))
line1 = average_line - std_line * 3
line2 = average_line + std_line * 3
print("长度3sigma的取值范围:", round(line1, 3), "--", round(line2, 3))
count2 = 0
for i in line_array:
    if line2 > i > line1:
        count2 = count2 + 1
print("米粒长度在3sigma内的数量为:", count2)

print("------------------------------")

cv2.imshow("fenGeTu", img)  # 显示标记后的图
cv2.waitKey()
cv2.imshow("yuZhiHuaTu: ", bw)
cv2.waitKey()

cv2.destroyAllWindows()

全局使用大津算法，对于米粒图片，效果不太好，一些角落的米粒都未被检测到，出现少数米粒“丢失”现象。 使用自适应阈值，将画面切成小块进行分别分割效果相对大津算法来说，效果较好。

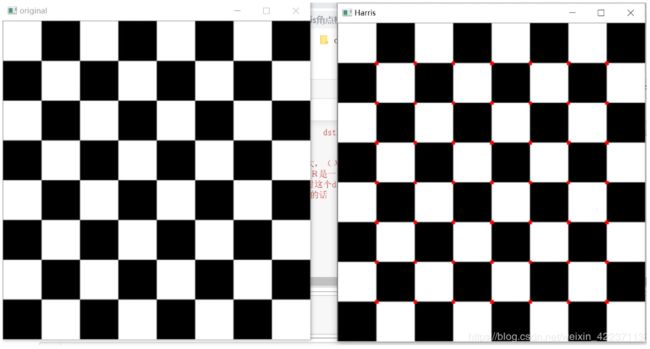
5 使用Harris角点检测算子检测棋盘格，并与上述结果比较

#  Harris 角点检测
# ref : opecv turial python
import cv2
import numpy as np

img = cv2.imread("./chessboard.jpg")
cv2.imshow("original",img)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) #图像灰度化
gray = np.float32(gray) #图像转换为float32

dst = cv2.cornerHarris(gray,2,3,0.04)#角点检测
#result is dilated for marking the corners, not important
dst = cv2.dilate(dst,None) #图像膨胀提升后续图像角点标注的清晰准确度

# 选择较大的相应函数R值的阈值，从而标定角点；阈值选择 [0.03,0.05]为佳
'''
img[dst>0.01*dst.max()]=[0,0,255]这段代码是什么意思吧　    dst>0.01*dst.max()这么多返回是满足条件的dst索引值　　根据索引值来设置这个点的颜色
这里是设定一个阈值　当大于这个阈值分数的都可以判定为角点
这里的dst其实就是一个个角度分数R组成的
当 λ 1 和 λ 2 都很大，并且 λ 1 ～λ 2 中的时，R 也很大，（λ 1 和 λ 2 中的最小值都大于阈值）说明这个区域是角点。
那么这里为什么要大于０．０１×ｄｓｔ.max()呢　注意了这里Ｒ是一个很大的值　我们选取里面最大的Ｒ
然后　只要dst里面的值大于百分之一的Ｒ的最大值　　那么此时这个dst的Ｒ值也是很大的　可以判定他为角点
也不一定要０．０１　　　可以根据图像自己选取不过如果太小的话　可能会多圈出几个不同的角点
'''
img[dst>0.03*dst.max()]=[0,0,255] #角点位置用红色标记

cv2.imshow('Harris',img)

cv2.waitKey()
cv2.destroyAllWindows()

6 使用棋盘格及自选风景图像，分别使用SIFT、FAST及ORB算子检测角点，并比较分析检测结果。

# Q5 使用棋盘格及自选风景图像，
# 分别使用SIFT、FAST及ORB算子检测角点，并比较分析检测结果
import cv2
import numpy as np

################## SIFT算子##################
"""
step1；构建初始图片
"""
# img_org = cv2.imread(r"D:\111111Python\AI\img_project\chapter2_homework\left12.jpg")
img_org = cv2.imread(r"D:\111111Python\AI\img_project\chapter2_homework\scences.jpg")
# 读取原图片的行、列、通道数
rows,cols,channels = img_org.shape
#沿着原图像顺指针旋转90度，并且缩减为原来的0.5
M = cv2.getRotationMatrix2D((cols/2, rows/2), 0, 0.5)
img_rot = cv2.warpAffine(img_org, M, (cols, rows))
# 转换成灰度图片
gray_org = cv2.cvtColor(img_org, cv2.COLOR_BGR2GRAY)
gray_rot = cv2.cvtColor(img_rot, cv2.COLOR_BGR2GRAY)
# 显示初始图片
# cmp_org = np.hstack((gray_org, gray_rot))# 水平拼接两个图片
# cv2.imshow("cmp_org",cmp_org)

"""
step2:提取特征点
"""
# 创建sift对象
sift = cv2.xfeatures2d_SIFT.create()
# 检测、计算特征点和描述子
kp_org,des_org =sift.detectAndCompute(gray_org,None)
kp_rot,des_rot =sift.detectAndCompute(gray_rot,None)
# 画出特征点
pic_org = cv2.drawKeypoints(gray_org, kp_org, None, (0, 0, 255))
pic_rot = cv2.drawKeypoints(gray_rot, kp_rot, None, (0, 0, 255))
# 显示特征点图片
# cmp_kp = np.hstack((pic_org, pic_rot))# 水平拼接两个图片
# cv2.imshow("cmp_org",cmp_kp)

"""
step3:特征匹配
"""
# # 创建BFMatcher对象
# bf = cv2.BFMatcher(cv2.NORM_L2)
# # 匹配特征点
# matches = bf.match(des_org,des_rot)
#
# # 画出匹配点
# img_match = cv2.drawMatches(gray_org, kp_org, gray_rot, kp_rot, matches[:100], None,flags=2)
# cv2.imshow("img_match", img_match)
"""
使用bf.match的两个图像检测的特征点错误比较多，简直不能直视
"""
# #######################################
# 设置FLANN 超参数
FLANN_INDEX_KDTREE = 0
# K-D树索引超参数
index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
# 搜索超参数
search_params = dict(checks=50)
# 初始化FlannBasedMatcher匹配器
flann = cv2.FlannBasedMatcher(index_params, search_params)
# 通过KNN的方式匹配两张图的描述子
matches = flann.knnMatch(des_org, des_rot, k=2)
print(matches)
# 筛选比较好的匹配点
good = []
for i, (m, n) in enumerate(matches):
    if m.distance < 0.6 * n.distance:
        good.append(m)
# 画出匹配点
img_nnmatch = cv2.drawMatches(img_org, kp_org, img_rot, kp_rot, good[100:130], None, flags=2)
cv2.imshow("SIFT-FLANN", img_nnmatch)
"""
使用FlannBasedMatcher匹配效果要好的太多
"""

cv2.waitKey()
cv2.destroyAllWindows()

不论是，缩放、旋转、平移，两张图的特征点都相同。但是很多并不是角点。 而且速度确实略慢。

################## sift改进版SURF算子 ##################
import cv2
import numpy as np

######step1；构建初始图片
img_org = cv2.imread(r"D:\111111Python\AI\img_project\chapter2_homework\left12.jpg")
# img_org = cv2.imread(r"D:\111111Python\AI\img_project\chapter2_homework\scences.jpg")
# 读取原图片的行、列、通道数
rows,cols,channels = img_org.shape
#沿着原图像顺指针旋转90度，并且缩减为原来的0.5
M = cv2.getRotationMatrix2D((cols/2, rows/2), 90, 0.5)
img_rot = cv2.warpAffine(img_org, M, (cols, rows))

######step2；提取图像特征点
hessian_threshold =  1000
# 创建检测算子
surf = cv2.xfeatures2d.SURF_create(hessian_threshold)
# 检测特征点、计算描述子
kp_org, des_org = surf.detectAndCompute(img_org, None)
kp_rot, des_rot = surf.detectAndCompute(img_rot, None)
######step3；特征匹配
# BFMacther类对象创建
# bf = cv2.BFMatcher(cv2.NORM_L1)
# # 匹配描述子
# matches = bf.match(des_org, des_rot)
# ## 此方法效果较差，出现较多的其他错误检测点，需要将hessian_threshold设置为很高才行。

# #######################################
# 设置FLANN 超参数
FLANN_INDEX_KDTREE = 0
# K-D树索引超参数
index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
# 搜索超参数
search_params = dict(checks=50)
# 初始化FlannBasedMatcher匹配器
flann = cv2.FlannBasedMatcher(index_params, search_params)
# 通过KNN的方式匹配两张图的描述子
matches = flann.knnMatch(des_org, des_rot, k=2)
# 筛选比较好的匹配点
good = []
for i, (m, n) in enumerate(matches):
    if m.distance < 0.6 * n.distance:
        good.append(m)


#####step4；画出相关匹配点
img_nnmatch = cv2.drawMatches(img_org, kp_org, img_rot, kp_rot, good[100:130], None, flags=2)
cv2.imshow("SURF", img_nnmatch)

cv2.waitKey()
cv2.destroyAllWindows()

感觉和纯sift相比，速度并没有提升那么快，但是相同情况下检测到特征点确实是少了比较多。不过相对来说还是比较准确。

################## FAST算子 ##################
import cv2
import numpy as np

######step1；构建初始图片
# img_org = cv2.imread(r"D:\111111Python\AI\img_project\chapter2_homework\left12.jpg")
img_org = cv2.imread(r"D:\111111Python\AI\img_project\chapter2_homework\scences.jpg")
# 读取原图片的行、列、通道数
rows,cols,channels = img_org.shape
#沿着原图像顺指针旋转90度，并且缩减为原来的0.5
M = cv2.getRotationMatrix2D((cols/2, rows/2), 90, 0.5)
img_rot = cv2.warpAffine(img_org, M, (cols, rows))

######step2；提取图像特征点
fast = cv2.FastFeatureDetector_create(threshold=40,
                                      nonmaxSuppression=True,
                                      type=cv2.FAST_FEATURE_DETECTOR_TYPE_9_16)
kp_org = fast.detect(img_org, None)
kp_rot = fast.detect(img_rot, None)
######step4；计算描述符
# 注意！！！！此处用的是 cv2.BRISK_create
br = cv2.BRISK_create()
kp_org, des_org = br.compute(img_org, kp_org)
kp_rot, des_rot = br.compute(img_rot, kp_rot)

######step3；特征匹配
# 创建BFMatcher对象
bf = cv2.BFMatcher(cv2.NORM_L2)
# 根据描述子匹配特征点
matches = bf.match(des_org, des_rot)
# 初始化Bruteforce匹配器
bf = cv2.BFMatcher()
# 通过KNN匹配两张图片的描述子
matches = bf.knnMatch(des_org, des_rot, k=2)
# 筛选比较好的匹配点
good = []
for i, (m, n) in enumerate(matches):
    if m.distance < 0.9 * n.distance:
        good.append(m)
# # 画出匹配点
# img3 = cv2.drawMatches(img_org, kp_org, img_rot, kp_rot, good, None, flags=2)
# cv2.imshow("FAST-BF", img3)

img3 = cv2.drawMatches(img_org, kp_org, img_rot, kp_rot, good, None, flags=2)
cv2.imshow("FAST-BF", img3)

FAST的特征点都是角点（以棋盘为例，其他算子都是在棋盘格子的中央，或者边缘地位），而且速度也是不慢的。但是检测到的特征点相对少一些。

################## ORB算子 ##################
import cv2
import numpy as np

######step1；构建初始图片
# img_org = cv2.imread(r"D:\111111Python\AI\img_project\chapter2_homework\left12.jpg")
img_org = cv2.imread(r"D:\111111Python\AI\img_project\chapter2_homework\scences.jpg")
# 读取原图片的行、列、通道数
rows,cols,channels = img_org.shape
#沿着原图像顺指针旋转90度，并且缩减为原来的0.5
M = cv2.getRotationMatrix2D((cols/2, rows/2), 90, 0.5)
img_rot = cv2.warpAffine(img_org, M, (cols, rows))

######step2；提取图像特征点
orb = cv2.ORB_create()
kp_org, des_org = orb.detectAndCompute(img_org,None)
kp_rot, des_rot = orb.detectAndCompute(img_rot,None)
######step3；特征匹配
bf = cv2.BFMatcher(cv2.NORM_L2)
# 通过KNN匹配两张图片的描述子
matches = bf.knnMatch(des_org,des_rot,k=2)
# 筛选较好的匹配点
good = []
for i, (m, n) in enumerate(matches):
    if m.distance < 1.1 * n.distance:
        good.append(m)
#####step4；画出相关匹配点
img2 = cv2.drawMatches(img_org, kp_org, img_rot, kp_rot, good, None, flags=2)
cv2.imshow("ORB-BF", img2)

cv2.waitKey()
cv2.destroyAllWindows()

ORB相对来说，速度较快，而且检测到的大部分都是角点。旋转、缩放操作并无较大影响。