建立线性回归模型的完整步骤（附代码）

---

O、简述

本案例所用数据为北京市统计局¹中的数据，欲了解 地区生产总值（因变量）与 全社会固定资产投资、社会消费品零售总额、进出口总值（三个自变量）之间的回归关系，即多元线性回归问题。
模型的建立，都是在一定的假设条件下成立的，线性回归自然也不会例外。其五大假设² 前提，具体见【数据诊断】部分。其中部分假设前提可以在数据准备好，也就是 建模前 就可以进行检验，包括：误差项ε服从正态分布、无多重共线性、线性相关性。来辅助初始模型的建立。当然，通过建模后，再诊断从而根据问题修正模型也是可以的。

像本博文梳理的目录结构，除了数据预处理环节，最后确定一个线性回归模型需要包括：建立模型、模型检验、模型诊断 及 针对诊断问题修正模型，不断重复这个过程，直到符合预期。
暂不对模型预测和部署做考虑，相对来说，建好模型后，预测只需按照建模过程中的数据准备工作，将待预测数据参照处理即可。

一、建立模型

本博文主要针对线性模型的一些主要方法步骤进行梳理，对于建模前的通用工作： 数据探索工作 内容暂不做考虑，后续会整理篇博文汇总这方面的相关要点。
简单点，直接进入建模环节。使用专门用于统计建模的第三方模块statsmodels，调用子模块中的ols函数进行建模。

# 导入第三方模块
import scipy.stats as stats
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn import model_selection
import statsmodels.api as sm

# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False

# 读取数据
gdp_data = pd.read_csv('北京市投资与GDP数据.csv',encoding='gbk',index_col=0)
# data.columns = ['全社会固定资产投资', '社会消费品零售总额', '进出口总值', '地区生产总值']
# 将数据集拆分为训练集和测试集
train,test = model_selection.train_test_split(gdp_data ,test_size=0.2,random_state=1234)
# 根据训练集train进行建模
model = sm.formula.ols('地区生产总值 ~ 全社会固定资产投资 + 社会消费品零售总额 + 进出口总值',data=train).fit()
print('模型的偏回归系数分别为：\n',model.params)

# 剔除测试集test中的 地区生产总值 变量，用剩下的自变量进行预测
test_x = test.drop(labels='地区生产总值',axis=1)
pred = model.predict(exog = test_x)
print('\n对比预测值和实际值的差异：\n',pd.DataFrame({'predict_y':pred,'real_y':test['地区生产总值']}))

回归模型已经构建完成，该模型的好与坏并没有相应的结论，也就是我们下一步要做的事情。

二、模型检验

模型检验包括：模型的显著性检验 和 模型回归系数的显著性检验。

• 模型的显著性检验 是指构成因变量的线性组合是否有效，即整个模型中是否至少存在一个自变量能够真正影响到因变量的波动。该检验是用来衡量模型的整体效应。
• 回归系数的显著性检验 是为了说明单个自变量在模型中是否有效，即自变量对因变量是否具有重要意义。这种检验则是出于对单个变量的肯定与否。

1 模型的显著性检验——F检验

# 导入模块
from scipy.stats import f

# 模型的F统计量值
print('模型的F统计量值：',model.fvalue)

# 计算F分布的理论值
p = model.df_model #统计变量个数
n = train.shape[0] # 观测个数
F_Theroy = f.ppf(q=0.95,dfn=p,dfd=n-p-1)
print('F分布的理论值：',F_Theroy)

模型的F统计量值： 478.94788648827745
F分布的理论值： 3.490294819497605

2 模型回归系数的显著性检验——t检验

关于系数的显著性检验，需要使用t检验法，构造t统计量。
在建立的模型中，其概览信息中就包含相应的各项指标值。简便起见，直接调用summary方法。

model.summary()

模型的概览信息包含三个部分:

• 第一部分主要是有关模型的信息
  • 模型的判决系数R2，用来衡量自变量对因变量的解释程度
  • 模型的F统计量值，用来检验模型的显著性
  • 模型的信息准则AIC或BIC，用来对比模型拟合效果的好坏等
• 第二部分主要包含偏回归系数的信息
  • 回归系数的估计值 coef、t统计量值、回归系数的置信区间 等
• 第三部分主要涉及模型误差项 $\epsilon$ 的有关信息
  • 杜宾－瓦特森统计量Durbin-Watson，用于检验误差项独立性
  • JB统计量，用于衡量误差项是否服从正态分布
  • 有关误差项偏度Skew和峰度Kurtosis的计算值等

三、数据诊断

统计学家在发明线性回归模型的时候就提出了一些假设前提，只有在满足这些假设前提的情况下，所得的模型才是合理的³。包括：

• 误差项ε服从正态分布
• 无多重共线性
• 线性相关性
• 误差项ε的独立性
• 方差齐性

除此之外，线性回归模型对异常值也是非常敏感的，以及缺失值等数据预处理的基础工作（后续会专门整理篇博文汇总这方面的相关处理手段）

1 正态性检验

模型的前提假设是对残差项要求服从正态分布，但是其实质就是要求因变量服从正态分布。关于正态性检验通常运用两类方法：

• 定性的图形法（直方图、PP图或QQ图）
• 定量的非参数法（Shapiro检验和K-S检验）

1.1 检验方法

1.1.1 直方图法

y = gdp_data['地区生产总值']
X = gdp_data[['全社会固定资产投资', '社会消费品零售总额', '进出口总值']]
# 绘制直方图
sns.distplot(a= y ,bins = 5, fit=stats.norm,norm_hist=True,
            hist_kws = {'color':'steelblue','edgecolor':'black'},
            kde_kws = {'color':'black','linestyle':'--','label':'核密度曲线'},
            fit_kws = {'color':'red','linestyle':':','label':'正态密度曲线'})
# 显示图例
plt.legend()
# 显示图形
plt.show()

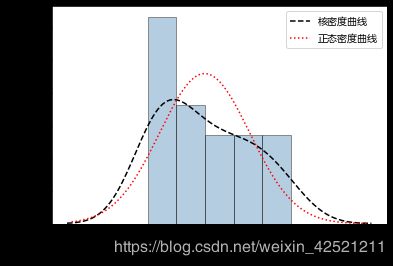
绘制了因变量地区生产总值的直方图、核密度曲线和理论正态分布的密度曲线，添加两条曲线的目的就是比对数据的实际分布与理论分布之间的差异。如果两条曲线近似或吻合，就说明该变量近似服从正态分布。

1.1.2 PP图与QQ图

• PP图的思想是比对正态分布的累计概率值和实际分布的累计概率值
• QQ图则比对正态分布的分位数和实际分布的分位数

判断变量是否近似服从正态分布的标准是：如果散点都比较均匀地散落在直线上，就说明变量近似服从正态分布，否则就认为数据不服从正态分布。

# 残差的正态性检验（PP和QQ）
pp_qq_plot = sm.ProbPlot(y)
# 绘制PP图
pp_qq_plot.ppplot(line = '45')
plt.title('P-P图')
# 绘制QQ图
pp_qq_plot.qqplot(line='q')
plt.title('Q-Q图')
plt.show()

1.1.3 Shapiro检验和K-S检验

这两种检验方法均属于非参数方法，它们的原假设被设定为变量服从正态分布，两者的最大区别在于适用的数据量不一样。

• 若数据量低于5000，则使用shapiro检验法比较合理
• 若数据量大于5000，则使用K-S检验法

scipy的子模块stats提供了专门的检验函数，分别是shapiro函数和kstest函数。
如果使用kstest函数对变量进行正态性检验，必须指定args参数，它用于传递被检验变量的均值和标准差。

# Shapiro检验
sp = stats.shapiro(y)
print("shapiro检验的统计量值：%.4f，对应的概率值p为：%.4f"%(sp))

shapiro检验的统计量值：0.9255，对应的概率值p为：0.1263

# K-S检验
# 为了应用K-S检验的函数kstest，这里随机生成正态分布变量rnorm和均匀分布变量runif
rnorm = np.random.normal(loc=5,scale=2,size=15000)
runif = np.random.uniform(low=1,high=50,size=15000)

# 正态性检验
ks_rnorm = stats.kstest(rvs=rnorm,args=(rnorm.mean(),rnorm.std()),cdf='norm')
ks_runif = stats.kstest(rvs=runif,args=(runif.mean(),runif.std()),cdf='norm')
print("rnorm 的 K-S检验的统计量值：%.4f，对应的概率值p为：%.4f"%(ks_rnorm))
print("runif 的 K-S检验的统计量值：%.4f，对应的概率值p为：%.4f"%(ks_runif))

rnorm 的 K-S检验的统计量值：0.0054，对应的概率值p为：0.7702
runif 的 K-S检验的统计量值：0.0631，对应的概率值p为：0.0000

1.2 校正方法

如果因变量的检验结果不满足正态分布时，需要对因变量做某种数学转换，使用比较多的转换方法有$log(y)$ 、$\sqrt{y}$、$\frac{1}{\sqrt{y}}$、$\frac{1}{y}$、$y^2$、$\frac{1}{y^2}$等。

2 多重共线性检验

多重共线性是指模型中的自变量之间存在较高的线性相关关系，它的存在会给模型带来严重的后果。包括：

• 由“最小二乘法”得到的偏回归系数无效
• 增大偏回归系数的方差
• 模型缺乏稳定性等

2.1 检验方法

2.1.1 方差膨胀因子VIF

关于多重共线性的检验可以使用方差膨胀因子VIF来鉴定。

• 如果VIF大于10，则说明变量间存在多重共线性；
• 如果VIF大于100，则表名变量间存在严重的多重共线性。

方差膨胀因子VIF的计算步骤如下：

1. 构造每一个自变量与其余自变量的线性回归模型:$x_1=c_0+{\alpha }_2{x}_2+...+{\alpha }_p{x}_p+\epsilon$
2. 根据如上线性回归模型得到相应的判决系数$R^2$，进而计算第一个自变量的方差膨胀因子VIF：$VI{F}_1=\frac{1}{1-R^2}$

# 导入statsmodels模块中的VIF函数
from statsmodels.stats.outliers_influence import variance_inflation_factor
# 自变量添加常数列
X = sm.add_constant(X)

# 构造空的数据框，用于存储VIF值
vif = pd.DataFrame()
vif['features'] = X.columns
vif['VIF Factor'] = [variance_inflation_factor(X.values,i) for i in range(X.shape[1])]
# 查看VIF值
vif

2.2 校正方法

如果发现变量之间存在多重共线性的话，可以考虑删除变量或者重新选择模型（如岭回归模型或LASSO模型）。

3 线性相关性检验

就是确保用于建模的自变量和因变量之间存在线性关系。

3.1 检验方法

关于线性关系的判断，可以使用Pearson相关系数和可视化方法进行识别。

3.1.1 Pearson相关系数

Pearson相关系数计算公式：
${\rho }_{x,y}=\frac{COV(x,y)}{\sqrt{D(x)}\sqrt{D(y)}}$

Pearson相关系数的计算可以直接使用数据框的corrwith“方法”，该方法最大的好处是可以计算任意指定变量间的相关系数。

# 计算因变量与每个自变量的相关系数
xy_corr = X.corrwith(y)
xy_corr

变量	Pearson相关系数
const	NaN
全社会固定资产投资	0.984303
社会消费品零售总额	0.995849
进出口总值	0.869777

3.1.2 可视化的方法——散点图矩阵

# 绘制散点图矩阵
sns.pairplot(data)
# 显示图形
plt.show()

4 残差的独立性检验

残差的独立性检验，实质上也是对因变量y的独立性检验，因为在线性回归模型的等式左右只有y和残差项ε属于随机变量，如果再加上正态分布，就构成了残差项独立同分布于正态分布的假设。

4.1 检验方法

4.1.1 DW检验（Durbin-Watson）

关于残差的独立性检验通常使用Durbin-Watson统计量值来测试。

• 如果DW值在2左右，则表明残差项之间是不相关的；
• 如果与2偏离的较远，则说明不满足残差的独立性假设。

对于DW统计量的值，它包含在模型的概览信息中，因此残差的独立性检验可以在建模后，通过模型的概览信息来查看。

model.summary()

5 方差齐性检验

方差齐性是要求模型残差项的方差不随自变量的变动而呈现某种趋势，否则，残差的趋势就可以被自变量刻画。如果残差项不满足方差齐性（方差为一个常数），就会导致偏回归系数不具备有效性，甚至导致模型的预测也不准确。所以，建模后需要验证残差项是否满足方差齐性。
关于方差齐性的检验，一般可以使用两种方法:

• 图形法（散点图）
• 统计检验法（BP检验和White检验）

5.1 检验方法

5.1.1 图形法-散点图

方差齐性是指残差项的方差不随自变量的变动而变动，所以只需要绘制残差与自变量之间的散点图，就可以发现两者之间是否存在某种趋势

fig = plt.figure(figsize=(15,5))
tu_num = 3 #子图数量
for i in range(tu_num):
    # 设置第一张子图的位置
    ax = plt.subplot2grid(shape=(1,tu_num),loc=(0,i))
    # 绘制散点图
    temp_x = train.ix[:,i]
    ax.scatter(temp_x,(model.resid-model.resid.mean())/model.resid.std())
    # 添加水平参考线
    ax.hlines(y=0,xmin=temp_x.min(),xmax=temp_x.max(),color='red',linestyles='--')
    #添加x轴和y轴标签
    ax.set_xlabel(train.columns[i])
    ax.set_ylabel('Std_Residual')
    
# #调整子图之间的水平间距和高度间距
# plt.subplots_adjust(hspace=0.1,wspace=0.3)
#显示子图   
plt.show()

标准化残差随自变量的变动而呈现一定趋势，所有的散点并未均匀的分布在参考线y=0的附近。可以说明模型的残差项不满足方差齐性的前提假设。

5.1.2 统计检验法（BP检验）

BP检验的原假设是残差的方差为一个常数，通过构造拉格朗日乘子LM统计量，实现方差齐性的检验。该检验可以借助于statsmodels模块中的het_breuschpagan函数完成。

# BP检验
bp_test = sm.stats.diagnostic.het_breuschpagan(model.resid,exog_het=model.model.exog)
                              
print('''
LM统计量：%.4f，
LM统计量对应的概率p值：%.4f，
F统计量：%.4f(用于检验残差平方项与自变量之间是否独立)，
F统计量的概率p值：%.4f(进一步验证残差项满足方差齐性的假设)
'''%(bp_test))

LM统计量：4.8883，
LM统计量对应的概率p值：0.1802，
F统计量：1.7597(用于检验残差平方项与自变量之间是否独立)，
F统计量的概率p值：0.2082(进一步验证残差项满足方差齐性的假设)

5.1.3 统计检验法（White检验）

# White检验
hw_test = sm.stats.diagnostic.het_white(model.resid,exog=model.model.exog)
                              
print('''
LM统计量：%.4f，
LM统计量对应的概率p值：%.4f，
F统计量：%.4f(用于检验残差平方项与自变量之间是否独立)，
F统计量的概率p值：%.4f(进一步验证残差项满足方差齐性的假设)
'''%(hw_test))

LM统计量：14.3086，
LM统计量对应的概率p值：0.1118，
F统计量：5.6398(用于检验残差平方项与自变量之间是否独立)，
F统计量的概率p值：0.0238(进一步验证残差项满足方差齐性的假设)

5.2 校正方法

如果模型的残差不满足齐性的话，可以考虑两类方法来解决：

1. 模型变换法
   对于模型变换法来说，主要考虑残差与自变量之间的关系。
   • 如果残差与某个自变量x成正比，则需将原模型的两边同除以$\sqrt{x}$；
   • 如果残差与某个自变量x的平方成正比，则需将原始模型的两边同除以x；
2. “加权最小二乘法”（可以使用statsmodels模块中的wls函数）
   对于加权最小二乘法来说，关键是如何确定权重，一般选择如下三种权重来进行对比测试：
   • 残差绝对值的倒数作为权重
   • 残差平方的倒数作为权重
   • 用残差的平方对数与自变量X重新拟合建模，并将得到的拟合值取指数，用指数的倒数作为权重

6 异常值检验

如果在建模过程中发现异常数据，需要对数据集进行整改，如删除异常值或衍生出是否为异常值的哑变量。对于线性回归模型来说，通常利用：

• 帽子矩阵
• DFFITS准则
• 学生化残差
• Cook距离
  进行异常点检测。

6.1 检验方法

6.1.1 帽子矩阵

帽子矩阵的设计思路就是考察第i个样本对预测值$\hat{y}$的影响大小。
帽子矩阵：$H=X(X^{\prime }X)X^{-1}{X}^{\prime }$。
判断样本是否为异常值的准则：$h_{ii}\ge \frac{2(p+1)}{n}$，
其中$h_{ii}$为帽子矩阵H的第i个主对角线元素，p为自变量个数，n为用于建模数据集的样本量。如果对角线元素满足上面的公式，则代表第i个样本为异常观测。

6.1.2 DFFITS准则

DFFITS准则借助于帽子矩阵，构造了另一个判断异常点的统计量：
$D_i(\sigma )=\sqrt{\frac{h_{ii}}{1-h_{ii}}}\frac{{\epsilon }_i}{\sigma \sqrt{1-h_{ii}}}$
其中${\epsilon }_i$为第i个样本点的预测误差，$\sigma$为误差项的标准差。在DFFITS准则的公式中，乘积的第二项实际上是学生化残差。
判断样本为异常值的准则：$\mid D_i(\sigma )\mid >2\sqrt{\frac{p+1}{n}}$

6.1.3 学生化残差

判断样本为异常值的准则：${\gamma }_i=\frac{{\epsilon }_i}{\sigma \sqrt{1-h_{ii}}}>2$

6.1.4 Cook距离

Cook距离是一种相对抽象的判断准则，无法通过具体的临界值判断样本是否为异常点，对于该距离，Cook统计量越大的点，其成为异常点的可能性越大。公式如下：
$Distanc{e}_i=\frac{1}{p+1}(\frac{h_{ii}}{1-h_{ii}}){{\gamma }_i}^2$

如果使用如上四种方法判别数据集的第i个样本是否为异常点，前提是已经构造好一个线性回归模型，然后基于get_influence方法获得四种统计量的值。

# 异常值检验
outliers = model.get_influence()

# 帽子矩阵
hat_mat = outliers.hat_matrix_diag
# DFFITS值
dffits = outliers.dffits[0]
# 学生化残差
resid_stu = outliers.resid_studentized_external
# cook距离
cook = outliers.cooks_distance[0]

# 合并四种异常值检验的统计量值
concat_four_out = pd.concat([pd.Series(hat_mat,name='帽子矩阵'),pd.Series(dffits,name='DFFITS值'),
                            pd.Series(resid_stu,name='学生化残差'),pd.Series(cook,name='Cook距离')],axis=1)

# 计算异常值比例，以学生会残差为例
outliers_ratio = sum(np.where(np.abs(resid_stu>2),1,0))/resid_stu.shape[0]
print("计算异常值比例，以学生会残差为准则，异常值比例为：",outliers_ratio)

# 挑选出无异常的观测点
none_outliers = train.ix[np.abs(resid_stu<=2),:]
none_outliers                  

计算异常值比例，以学生会残差为准则，异常值比例为： 0.0625。
之后可根据无异常值再进行建模过程。

四、小结

如你所看到的，很多诊断结果我们只是列了结果，没有给出相应的结论或者说明。这是因为小编想着重记录的是线性回归模型建模过程中，应该包括的一些必不可少的步骤及对应的python实现方法。如有不明之处，我们可评论区交流学习。

---

1. 北京市统计局 ↩︎

2. 计量经济学 / 张晓峒著. —北京：清华大学出版社，2017(2018.9重印) ↩︎

3. 从零开始学Python数据分析与挖掘／刘顺祥著．—北京：清华大学出版社，2018ISBN 978-7-302-50987-5 ↩︎