lgb--贝叶斯调参及代码

概述

贝叶斯优化问题有四个部分：

目标函数 objective()：我们想要最小化的内容，在这里，目标函数是机器学习模型使用该组超参数通过交叉验证计算损失值。

域空间 space：要搜索的超参数的取值范围。

优化算法 algo：构造替代函数并选择下一个超参数值进行评估的方法。

结果历史记录 result：来自目标函数评估的存储结果，包括超参数和验证集上的损失。

1.目标函数 objective()：

def objective(params, n_flods=5):
    # 记录迭代次数
    global ITERATION
    ITERATION += 1
  
    params['boosting_type'] = params['boosting_type']['boosting_type']
    for param in ['n_estimators','max_depth','num_leaves','min_child_samples','subsample_freq']:
        params[param] = int( params[param])
    
    start_time = timer()
    
    #cv_results = lgb.cv(params=params,train_set=train_set, num_boost_round=100, nfold=n_flods,
    #                    early_stopping_rounds=100, metrics='auc', seed=50,verbose_eval=False)
    model_lgb = lgb.LGBMClassifier(boosting_type=params['boosting_type'],
                    objective = params['objective'],
                    metric = 'auc', 
                    subsample_freq=params['subsample_freq'],
                    learning_rate= params['learning_rate'],
                    n_estimators = params['n_estimators'],
                    max_depth = params['max_depth'],
                    bagging_fraction = params['bagging_fraction'],
                    colsample_bytree = params['colsample_bytree'],
                    min_child_samples = params['min_child_samples'],
                    reg_alpha = params['reg_alpha'],
                    reg_lambda = params['reg_lambda'],
                    seed=5000,
                    n_jobs=4)
    auc= cross_val_score(model_lgb,x_train_train,y_train_train,cv=n_flods,scoring="roc_auc").mean()
    
    end_time = timer()
    run_time = end_time - start_time
    
    # 找出cv中最大的平均auc,因为Hyperopt需要返回最小值loss，所以用 1-auc来代替
    loss = 1 - auc
    
    # 最大平均auc对应的提升术的迭代次数
    n_estimators = int(params['n_estimators'])
    
    # 把关心的结果输出到csv文件
    of_connection = open(out_file, 'a')
    writer = csv.writer(of_connection)
    writer.writerow([loss,params,ITERATION,n_estimators,run_time])
    
    return_dict = {'loss':loss, 'params':params, 'iteration':ITERATION,
                   'estimators':n_estimators,'train_time':run_time,'status':STATUS_OK}
    return return_dict

注：

1.object()函数通过交叉验证计算损失值

2.通过lgb.cv计算loss值

    cv_results = lgb.cv(..., metrics = 'auc') ，

    best_score = np.max(cv_results['auc-mean'])

    loss = 1 - best_score

3.通过cross_val_score计算loss值

     model_lgb = lgb.LGBMClassifier(..., metric = 'auc' )

     auc= cross_val_score(model_lgb,...,scoring="roc_auc").mean()

     loss = 1 - auc 

2.域空间 space：

space = {
    # 'class_weight': hp.choice('class_weight', [None, 'balanced']),
    'boosting_type': hp.choice('boosting_type', [{'boosting_type': 'gbdt'}]),
    'num_leaves': hp.quniform('num_leaves', 20, 200, 5),
    'learning_rate': hp.choice('learning_rate',[0.1]),
    'min_child_samples': hp.quniform('min_child_samples', 40, 401, 20),
    'reg_alpha': hp.uniform('reg_alpha', 0.0, 1.0),
    'reg_lambda': hp.uniform('reg_lambda', 0.0, 1.0),
    'subsample_freq':hp.choice('subsample_freq',[1]),
    'colsample_bytree':hp.quniform('colsample_bytree',0.7, 1.0, 0.1),
    'bagging_fraction':hp.quniform('bagging_fraction', 0.7, 1.0, 0.1),
    'max_depth': hp.choice('max_depth',[5, 6, 7, 8]),
    'objective': hp.choice('objective', ['binary']), 
    'n_estimators': hp.quniform('n_estimators',50,201,20)
}

注：

Hyperopt 提供了10种定义参数空间的分布(详情可参考https://github.com/hyperopt/hyperopt/wiki/FMin):

hp.choice(label, options): 离散的均匀分布, 适用于参数中类别的选择, 如"boosting_type"中选"gbdt", "dart", "goss";

hp.randint(label, upper): [0, upper) 定义域的整数均分布;

hp.uniform(label, low, high): [low, high] 定义域的均匀分布;

hp.quniform(label, low, high, q): round(uniform(low, high) / q) * q;

hp.loguniform(label, low, high): exp(uniform(low, high)), 适用于夸量级的参数, 如learning_rate;

hp.qloguniform(label, low, high, q): round(exp(uniform(low, high)) / q) * q;

hp.normal(label, mu, sigma): 正态分布;

hp.qnormal(label, mu, sigma, q): round(normal(mu, sigma) / q) * q;

hp.lognormal(label, mu, sigma): exp(normal(mu, sigma));

hp.qlognormal(label, mu, sigma, q): round(exp(normal(mu, sigma)) / q) * q;

3.优化算法 algo

from hyperopt import tpe

from hyperopt import Trials
TPE + MEI 算法
先验假设(TPE)和采集函数(MEI)
tpe_algorithm = tpe.suggest

利用 Trials 实例存储
bayes_trials = Trials()

from hyperopt import fmin
 best = fmin(fn = objective, space = space, algo = tpe.suggest, 
                    max_evals = MAX_EVALS, trials = bayes_trials, rstate = np.random.RandomState(50),verbose=1)

注：

fn ：目标函数

space：超参数空间

algo：优化算法

max_evals：调参过程迭代次数

trials：实例存储

rstate：随机选取数据

verbose：日志冗长度，输出详细信息

4.结果历史记录 result：

columns=['loss', 'params', 'iteration', 'estimators', 'train_time']

注：

记录迭代过程中的模型信息及迭代信息

总结：

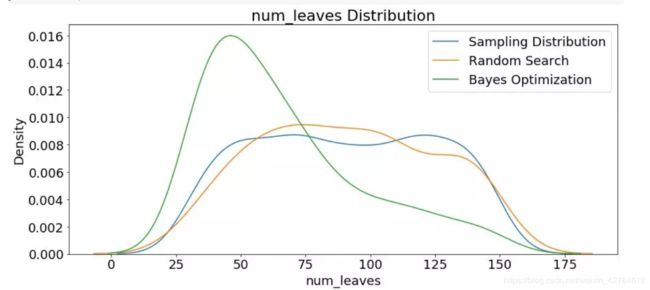
1.超参数分布num_leves

随机搜索与原样本分布如其所愿基本保持一直, 而贝叶斯在代理模型TPE的引导下"num_leaves"分布变化巨大.

2AUC演化趋势

Bayes确实在循序渐进地优化结果而随机搜索也的确很随机