《算法(第四版)》2.2部分习题
算法之路漫漫,还只是个初学者,仅做笔记,有很多不好的地方提前致歉。
代码都已上传到git/github,其中包括在力扣上的一些题解(目前较少)以及笔记。
git:https://gitee.com/yayako/algorithm.git
github:https://github.com/yayakoBlessing/algorithm.git
官方库jar包已上传至百度云
链接:https://pan.baidu.com/s/182L-CZHq–NimCPii95zAg
提取码:xgxb
前面的练习题官方网站上基本都有解答
https://algs4.cs.princeton.edu/22mergesort/
文章目录
- 算法比较 封装
- 2.2.8
- 题目
- 解答
- 代码实现
- 2.2.10
- 题目
- 评估
- 代码实现
- 2.2.11
- 题目
- 评估
- 代码实现
- 加快小数组的排序速度
- 检测数组是否已经有序
- 通过在递归中交换参数来避免数组复制
- 三合一
- *2.2.12 未解决
- 题目
- 评估
- 代码实现
- 2.2.14
- 题目
- 代码实现
- 2.2.15
- 题目
- 代码实现
- 2.2.16
- 题目
- 评估
- 代码实现
- 2.2.17
- 题目
- 评估
- 代码实现
- *2.2.18 未解决
- 题目
- 评估
- 代码实现
- 2.2.19
- 题目
- 评估
- 代码实现
- 2.2.20
- 题目
- 解答
- 代码实现
- 2.2.21
- 题目
- 解答
- 代码实现
- 2.2.22
- 题目
- 分析
- 代码实现
- 2.2.23
- 题目
- 评估
- 代码实现
- 2.2.24
- 题目
- 评估
- 代码实现
- *2.2.25 未解决
- 题目
- 评估
- 代码实现
- 2.2.26
- 题目
- 评估
- 代码实现
- 2.2.27
- 题目
- 评估
- 代码实现
- 2.2.28
- 题目
- 评估
- 代码实现
- 2.2.29
- 题目
- 评估
- 参考
算法比较 封装
/**
* 算法比较(基于不同算法对同一数组的排序的用时比较)
*
* @param s 名称
* @param baseSorts 算法类
*/
public static void timeRandomInput(String[] s, BaseSort[] baseSorts) {
List<Comparable[]> a = new ArrayList<>(T);
Comparable[] b;
double[] total, pre = new double[s.length];
int n;
// 生成从100~100000数量级长度的测试数组
for (int i = 2; i <= 5; i++) {
n = (int) Math.pow(10, i);
System.out.println();
System.out.println("ArraySize = " + n);
// 每个数量级的排序都要分别进行T次,所以需要初始化T个相同长度的不同数组
for (int j = 0; j < T; j++) {
b = ArrayGenerate.random(n);
a.add(b);
}
total = SortCompare.compare(baseSorts, a, n);
for (int k = 0; k < baseSorts.length; k++) {
System.out.println(s[k] + ":" + total[k] + "\tnow/pre = " + total[k] / pre[k]);
pre[k] = total[k];
}
a.clear();
}
}
/**
* 综合比较
*
* @param baseSorts 需要进行比较的各算法类型
* @param a 排序对象数组
* @param n 数组长度
* @return 用时数组
*/
public static double[] compare(BaseSort[] baseSorts, List<Comparable[]> a, int n) {
Comparable[] b;
int j;
double[] total = new double[baseSorts.length];
for (int i = 0; i < T; i++) {
b = new Comparable[n];
j = 0;
for (BaseSort baseSort : baseSorts) {
System.arraycopy(a.get(i), 0, b, 0, n);
total[j++] = SortCompare.time(baseSort, b);
}
}
return total;
}
/** 构造随机数组 */
public static Comparable[] random(int n) {
Comparable[] a = new Comparable[n];
for (int i = 0; i < n; i++) a[i] = Math.random() * 100;
return a;
}
2.2.8
题目
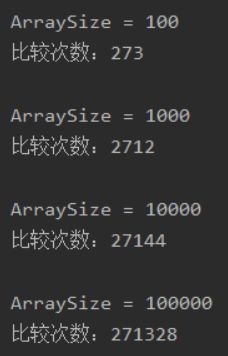
假设将算法2.4修改为:只要a[mid]<=a[mid+1]就不调用merge()方法,请证明用归并排序处理一个已经有序的数组所需的比较次数是线性级别的。
解答
理论上,根据命题F的证明过程有,当N为2的幂时,比较次数将满足递归T(N)= 2 T(N / 2)+1,其中T(1)= 0。
代码实现
/**
* 假设将算法2.4修改为:只要a[mid]<=a[mid+1]就不调用merge()方法,请证明用归并排序处理一个已经有序的数组所需的比较次数是线性级别的。
*
* @author cyy
*/
public class ex8 {
private static Comparable[] aux;
private static int ctime;
public static void main(String[] args) {
for (int n = 100; n <= 100000; n *= 10) {
ctime = 0;
sort(ArrayGenerate.inorder(n));
System.out.println("\nArraySize = " + n + "\n比较次数:" + ctime);
}
}
public static void sort(Comparable[] a) {
aux = new Comparable[a.length];
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int l, int r) {
ctime++;
if (l >= r) return;
int mid = (l + r) / 2;
sort(a, l, mid);
sort(a, mid + 1, r);
if (Common.less(a[mid], a[mid + 1])) return;
merge(a, l, mid, r);
}
private static void merge(Comparable[] a, int l, int mid, int r) {
int i = l, j = mid + 1;
System.arraycopy(a, l, aux, l, r - l + 1);
ctime++;
for (int k = l; k <= r; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > r) a[k] = aux[i++];
else if (Common.less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
}
2.2.10
题目
*快速归并。*实现一个merge()方法,按降序将a[]的后半部分复制到aux[],然后将其归并回a[]中。这样就可以去掉内循环中检测某半边是否用尽的代码。注意:这样的排序产生的结果是不稳定的(请见2.5.1.8节)。
评估
代码实现
/**
* 快速归并。
*
* 实现一个merge()方法,按降序将a[]的后半部分复制到aux[],然后将其归并回a[]中。 这样就可以去掉内循环中检测某半边是否用尽的代码。
* 注意:这样的排序产生的结果是不稳定的(请见2.5.1.8节)。
*
* @author cyy
*/
public class ex10 {
private static Comparable[] aux;
public static void main(String[] args) {
Comparable[] a = {1, 5, 9, 11, 2, 4, 12, 13};
aux = new Comparable[a.length];
merge(a, 0, (a.length - 1) / 2, a.length - 1);
Common.print(a);
}
private static void merge(Comparable[] a, int l, int mid, int r) {
for (int i = l; i <= mid; i++) aux[i] = a[i];
for (int i = mid + 1; i <= r; i++) aux[i] = a[r + mid - i + 1];
int i = l, j = r;
for (int k = l; k <= r; k++) {
if (Common.less(aux[i], aux[j])) a[k] = aux[i++];
else a[k] = aux[j--];
}
}
}
2.2.11
题目
*改进。*实现2.2.2节所述的对归并排序的三项改进:加快小数组的排序速度,检测数组是否已经有序以及通过在递归中交换参数来避免数组复制。
评估
代码实现
-
加快小数组的排序速度
设置一个界限
LIMIT,当要对小于这个LIMIT的数组进行排序时,直接调用插入排序private static final int LIMIT = 15; // 界限 private void sort(Comparable[] a, int l, int r) { if (r - l + 1 < LIMIT) { // 对小规模子数组使用插入排序 insertion(a, l, r); return; } int mid = (l + r) / 2; sort(a, l, mid); sort(a, mid + 1, r); merge(a, l, mid, r); } private void insertion(Comparable[] a, int l, int r) { for (int i = l + 1; i <= r; i++) for (int j = i; j > l && Common.less(a[j], a[j - 1]); j--) Common.exch(a, j - 1, j); } -
检测数组是否已经有序
就是题2.2.8中的方法,当测试数组满足
a[mid]<=a[mid+1]时,直接return,不调用merge方法private void sort(Comparable[] a, int l, int r) { if (l >= r) return; int mid = (l + r) / 2; sort(a, l, mid); sort(a, mid + 1, r); if (Common.less(a[mid], a[mid + 1])) return; // 测试数组已经有序跳过merge方法 merge(a, l, mid, r); } -
通过在递归中交换参数来避免数组复制
这个很神奇,就这几个字理解起来优点绕,但是理解后会发现其实就是这几个字。
通过在递归中交换两个数组来避免数组复制
-
原版中
一个是主数组对象a,一个是辅助数组对象aux。
我们是先将a中要比较的元素复制到aux中,再通过对aux中的元素进行比较重新存入a中。
-
改进后
这个改进的思路则是通过交换两个数组的地位。
一个是主数组对象dst,一个是辅助数组对象src。
在
merge方法中每次都是把src数组中的元素进行比较再存入dst数组中,但是在递归调用sort方法时交换两个数组的传参位置来实现两个数组的地位交换
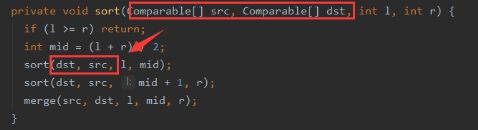
但其实输出结果会发现其实就是对同一串数组进行排序,在每次
merge方法中输出src数组和dst数组,实际上 每一次merge中的src都是上一次sort中修改后,即半边排序完后的dstprivate void sort(Comparable[] src, Comparable[] dst, int l, int r) { if (l >= r) return; int mid = (l + r) / 2; sort(dst, src, l, mid); sort(dst, src, mid + 1, r); merge(src, dst, l, mid, r); } private void merge(Comparable[] src, Comparable[] dst, int l, int mid, int r) { int i = l, j = mid + 1; // System.arraycopy(a, l, aux, l, r - l + 1); 避免数组复制 for (int k = l; k <= r; k++) { if (i > mid) dst[k] = src[j++]; else if (j > r) dst[k] = src[i++]; else if (Common.less(src[i], src[j])) dst[k] = src[i++]; else dst[k] = src[j++]; } }
-
-
三合一
/**
* 改进。
*
* 实现2.2.2节所述的对归并排序的三项改进:加快小数组的排序速度,检测数组是否已经有序以及通过在递归中交换参数来避免数组复制。
*
* @author cyy
*/
public class ex11 implements BaseSort {
private static final int LIMIT = 15;
@Override
public void sort(Comparable[] a) {
Comparable[] aux = a.clone();
sort(aux, a, 0, a.length - 1);
}
private void sort(Comparable[] src, Comparable[] dst, int l, int r) {
if (r - l + 1 < LIMIT) { // 对小规模子数组使用插入排序
insertion(dst, l, r);
return;
}
int mid = (l + r) / 2;
sort(dst, src, l, mid);
sort(dst, src, mid + 1, r);
if (Common.less(src[mid], src[mid + 1])) return; // 测试数组已经有序跳过merge方法
merge(src, dst, l, mid, r);
}
private void merge(Comparable[] src, Comparable[] dst, int l, int mid, int r) {
int i = l, j = mid + 1;
for (int k = l; k <= r; k++) { // 交换角色——将src进行比较后复制给a,将数据从辅助数组排序到输入数组
if (i > mid) dst[k] = src[j++];
else if (j > r) dst[k] = src[i++];
else if (Common.less(src[i], src[j])) dst[k] = src[i++];
else dst[k] = src[j++];
}
}
private void insertion(Comparable[] a, int l, int r) {
for (int i = l + 1; i <= r; i++)
for (int j = i; j > l && Common.less(a[j], a[j - 1]); j--) Common.exch(a, j - 1, j);
}
}
*2.2.12 未解决
题目
*次线性的额外空间。*用大小M将数组分为N/M块(简单起见,设M是N的约数)。实现一个归并方法,使之所需的额外空间减少到max(M,N/M):(i)可以先将一个块看做一个元素,将块的第一个元素作为块的主键,用选择排序将块排序;(ii)遍历数组,将第一块和第二块归并,完成后将第二块和第三块归并,等等。
评估
代码实现
2.2.14
题目
归并有序的队列。编写一个静态方法,将两个有序的队列作为参数,返回一个归并后的有序队列。
代码实现
/**
* 归并有序的队列。
*
* 编写一个静态方法,将两个有序的队列作为参数,返回一个归并后的有序队列。
*
* @author cyy
*/
public class ex14 {
public static void main(String[] args) {
Queue<Comparable> queue1 = initQueue(100);
Queue<Comparable> queue2 = initQueue(150);
System.out.println(isSorted(merge(queue1, queue2)));
}
private static boolean isSorted(Queue<Comparable> queue) {
Comparable a = queue.poll();
while (!queue.isEmpty()) {
if (Common.less(queue.element(), a)) return false;
a = queue.poll();
}
return true;
}
private static Queue<Comparable> initQueue(int n) {
Queue<Comparable> queue = new ArrayDeque<>(n);
queue.addAll(Arrays.asList(ArrayGenerate.inorder(n)));
return queue;
}
private static Queue<Comparable> merge(Queue<Comparable> queue1, Queue<Comparable> queue2) {
int n = queue1.size() + queue2.size();
Queue<Comparable> res = new ArrayDeque<>(n);
Comparable i = queue1.peek(), j = queue2.peek();
while (!queue1.isEmpty() || !queue2.isEmpty()) {
if (queue1.isEmpty()) res.add(queue2.remove());
else if (queue2.isEmpty()) res.add(queue1.remove());
else if (Common.less(j, i)) {
res.add(queue2.remove());
j = queue2.peek();
} else {
res.add(queue1.remove());
i = queue1.peek();
}
}
return res;
}
private static void print(Queue<Comparable> queue) {
while (!queue.isEmpty()) System.out.println(queue.poll());
}
}
2.2.15
题目
*自底向上的有序队列归并排序。*用下面的方法编写一个自底向上的归并排序:给定N个元素,创建N个队列,每个队列包含其中一个元素。创建一个由这N个队列组成的队列,然后不断用练习2.2.14中的方法将队列的头两个元素归并,并将幸福空间要重新加入到队列结尾,直到队列的队列只剩下一个元素为止。
代码实现
/**
* 自底向上的有序队列归并排序。
*
* 用下面的方法编写一个自底向上的归并排序:给定N个元素,创建N个队列,每个队列包含其中一个元素。
* 创建一个由这N个队列组成的队列,然后不断用练习2.2.14中的方法将队列的头两个元素归并,并将结果重新加入到队列结尾,直到队列的队列只剩下一个元素为止。
*
* @author cyy
*/
public class ex15 {
public static void main(String[] args) {
Comparable[] a = ArrayGenerate.random(100);
Queue<Queue<Comparable>> queues = createNQueue(a);
Queue<Comparable> i, j;
while (queues.size() > 1) {
i = queues.poll();
j = queues.poll();
queues.add(ex14.merge(i, j));
}
System.out.println(ex14.isSorted(queues.element()));
}
private static Queue<Queue<Comparable>> createNQueue(Comparable[] a) {
Queue<Queue<Comparable>> queues = new ArrayDeque<>(a.length);
Queue<Comparable> queue;
for (Comparable c : a) {
queue = new ArrayDeque<>(1);
queue.add(c);
queues.add(queue);
}
return queues;
}
}
2.2.16
题目
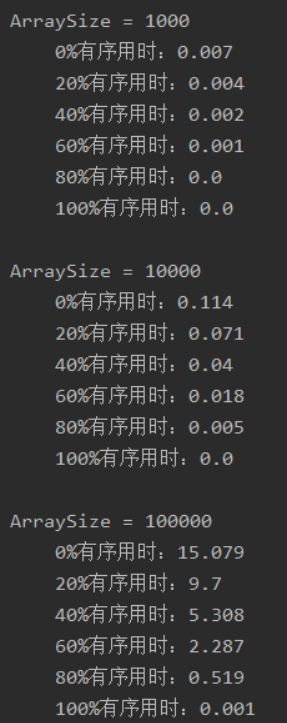
*自然的归并排序。*编写一个自底向上的归并排序,当需要将两个子数组排序时能够利用数组中已经有序的部分。首先找到一个有序的子数组(移动指针直到当前元素比上一个元素小为止),然后再找出另一个并将它们归并。根据数组大小和数组中递增子数组的最大长度分析算法的运行时间。
评估
代码实现
首先找到一个有序的子数组(移动指针直到当前元素比上一个元素小为止),用mid记录位置,再往下找出另一个有序子数组,并将它们归并,重新记录mid位置,再往后。
值得注意的两点
- 第一次找到有序数组是不用马上进行归并的,所以设了个flag来判断
- 当数组归并到只剩下两个有序的子数组时,循环将面临结束,因为a已经到达数组末尾,但无法确定下一个临界,因此在最后还需要对最后的有序子数组进行归并。即 1,2,6,4,5 这种情况。
package alg4.sort.ex.chap2.section2;
import alg4.sort.basesort.BaseSort;
import alg4.sort.utils.ArrayGenerate;
import alg4.sort.utils.Common;
import alg4.sort.utils.SortCompare;
/**
* 自然的归并排序。
*
* 编写一个自底向上的归并排序,当需要将两个子数组排序时能够利用数组中已经有序的部分。
*
*
首先找到一个有序的子数组(移动指针直到当前元素比上一个元素小为止),然后再找出另一个并将它们归并。
*
*
根据数组大小和数组中递增子数组的最大长度分析算法的运行时间。
*
* @author cyy
*/
public class ex16 implements BaseSort {
private static Comparable[] aux;
public static void main(String[] args) {
Comparable[] a;
for (int i = 100; i <= 100000; i *= 10) {
System.out.println("ArraySize = " + i);
for (int j = 0; j <= 100; j += 20) {
a = ArrayGenerate.partialInOrder(i, (double) j / 100);
System.out.println("\t" + j + "%有序用时:" + SortCompare.time(new ex16(), a));
}
System.out.println();
}
}
private static void merge(Comparable[] a, int l, int mid, int r) {
int i = l, j = mid + 1;
System.arraycopy(a, 0, aux, 0, r - l + 1);
if (!Common.less(a[l], a[r])) { // 后一个有序块的最大值 大于 首元素
System.arraycopy(aux, j, a, 0, r - mid);
System.arraycopy(aux, 0, a, r - mid, j);
} else {
for (int k = l; k <= r; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > r) a[k] = aux[i++];
else if (Common.less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
}
@Override
public void sort(Comparable[] a) {
aux = new Comparable[a.length];
int flag = -1, mid = 0;
for (int i = 1; i < a.length; i++) {
if (Common.less(a[i], a[i - 1])) {
if (flag == 1) merge(a, 0, mid, i - 1);
mid = i - 1;
flag = 1;
}
}
// 对最后的有序子数组进行归并
if (a.length > 1 && Common.less(a[mid + 1], a[mid])) merge(a, 0, mid, a.length - 1);
}
}
package alg4.sort.ex.chap2.section2;
import alg4.sort.basesort.BaseSort;
import alg4.sort.utils.ArrayGenerate;
import alg4.sort.utils.Common;
import alg4.sort.utils.SortCompare;
/**
* 自然的归并排序。
*
* 编写一个自底向上的归并排序,当需要将两个子数组排序时能够利用数组中已经有序的部分。
*
*
首先找到一个有序的子数组(移动指针直到当前元素比上一个元素小为止),然后再找出另一个并将它们归并。
*
*
根据数组大小和数组中递增子数组的最大长度分析算法的运行时间。
*
* @author cyy
*/
public class ex16 implements BaseSort {
private static Comparable[] aux;
public static void main(String[] args) {
Comparable[] a;
for (int i = 100; i <= 100000; i *= 10) {
System.out.println("ArraySize = " + i);
for (int j = 0; j <= 100; j += 20) {
a = ArrayGenerate.partialInOrder(i, (double) j / 100);
System.out.println("\t" + j + "%有序用时:" + SortCompare.time(new ex16(), a));
}
System.out.println();
}
}
private static void merge(Comparable[] a, int l, int mid, int r) {
int i = l, j = mid + 1;
System.arraycopy(a, 0, aux, 0, r - l + 1);
if (!Common.less(a[l], a[r])) { // 后一个有序块的最大值 大于 首元素
System.arraycopy(aux, j, a, 0, r - mid);
System.arraycopy(aux, 0, a, r - mid, j);
} else {
for (int k = l; k <= r; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > r) a[k] = aux[i++];
else if (Common.less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
}
@Override
public void sort(Comparable[] a) {
aux = new Comparable[a.length];
int flag = -1, mid = 0;
for (int i = 1; i < a.length; i++) {
if (Common.less(a[i], a[i - 1])) {
if (flag == 1) merge(a, 0, mid, i - 1);
mid = i - 1;
flag = 1;
}
}
// 对最后的有序子数组进行归并
if (a.length > 1 && Common.less(a[mid + 1], a[mid])) merge(a, 0, mid, a.length - 1);
}
}
package alg4.sort.ex.chap2.section2;
import alg4.sort.basesort.BaseSort;
import alg4.sort.utils.ArrayGenerate;
import alg4.sort.utils.Common;
import alg4.sort.utils.SortCompare;
/**
* 自然的归并排序。
*
* 编写一个自底向上的归并排序,当需要将两个子数组排序时能够利用数组中已经有序的部分。
*
*
首先找到一个有序的子数组(移动指针直到当前元素比上一个元素小为止),然后再找出另一个并将它们归并。
*
*
根据数组大小和数组中递增子数组的最大长度分析算法的运行时间。
*
* @author cyy
*/
public class ex16 implements BaseSort {
private static Comparable[] aux;
public static void main(String[] args) {
Comparable[] a;
for (int i = 100; i <= 100000; i *= 10) {
System.out.println("ArraySize = " + i);
for (int j = 0; j <= 100; j += 20) {
a = ArrayGenerate.partialInOrder(i, (double) j / 100);
System.out.println("\t" + j + "%有序用时:" + SortCompare.time(new ex16(), a));
}
System.out.println();
}
}
private static void merge(Comparable[] a, int l, int mid, int r) {
int i = l, j = mid + 1;
System.arraycopy(a, 0, aux, 0, r - l + 1);
if (!Common.less(a[l], a[r])) { // 后一个有序块的最大值 大于 首元素
System.arraycopy(aux, j, a, 0, r - mid);
System.arraycopy(aux, 0, a, r - mid, j);
} else {
for (int k = l; k <= r; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > r) a[k] = aux[i++];
else if (Common.less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
}
@Override
public void sort(Comparable[] a) {
aux = new Comparable[a.length];
int flag = -1, mid = 0;
for (int i = 1; i < a.length; i++) {
if (Common.less(a[i], a[i - 1])) {
if (flag == 1) merge(a, 0, mid, i - 1);
mid = i - 1;
flag = 1;
}
}
// 对最后的有序子数组进行归并
if (a.length > 1 && Common.less(a[mid + 1], a[mid])) merge(a, 0, mid, a.length - 1);
}
}
/**
* 部分有序数组(有序部分在后面)
*
* @param n 数组长度
* @param p 有序占比
*/
public static Comparable[] partialInOrder(int n, double p) {
Comparable[] a = inorder(n);
int i;
for (i = 0; i < n - n * p; i++) a[i] = Math.random() * 100;
return a;
}
2.2.17
题目
*链表排序。*实现对链表的自然排序(这是将链表排序的最佳方法,因为它不需要额外的空间,且运行时间是线性对数级别的)。
评估
写的太杂,不建议看。
我确确实实把链表都还给老师了orz
代码实现
package alg4.sort.ex.chap2.section2;
import alg4.datastructures.LinkList;
import alg4.datastructures.ListNode;
import alg4.sort.basesort.BaseSort;
import alg4.sort.utils.ArrayGenerate;
import alg4.sort.utils.Common;
import alg4.sort.utils.SortCompare;
import static alg4.datastructures.LinkList.creLLR;
/**
* 链表排序。
*
* 实现对链表的自然排序(这是将链表排序的最佳方法,因为它不需要额外的空间,且运行时间是线性对数级别的)。
*
* @author cyy
*/
public class ex17 implements BaseSort {
public static void main(String[] args) {
Comparable[] a;
for (int i = 100; i <= 10000; i *= 10) {
System.out.println("ArraySize = " + i);
for (int j = 0; j <= 100; j += 20) {
a = ArrayGenerate.partialInOrder(i, (double) j / 100);
System.out.println("\t" + j + "%有序用时:" + SortCompare.time(new ex17(), a));
}
System.out.println();
}
}
private static ListNode<Comparable> merge(
LinkList<Comparable> linkList,
ListNode<Comparable> l,
ListNode<Comparable> mid,
ListNode<Comparable> r) {
if (!Common.less(l.data, r.data)) { // 后一个有序块的最大值 大于 首元素
linkList.head = mid.next;
mid.next = r.next;
r.next = l;
return mid;
} else {
ListNode<Comparable> i = l, j = mid.next;
ListNode<Comparable> node = new ListNode<>();
ListNode<Comparable> pre = node, end = r.next;
while (true) {
if (i == mid.next) {
node.next = j;
r.next = end;
node = node.next;
break;
} else if (j == r.next) {
node.next = i;
mid.next = end;
node = node.next;
break;
} else if (Common.less(j.data, i.data)) {
node.next = j;
j = j.next;
} else {
node.next = i;
i = i.next;
}
node = node.next;
}
linkList.head = pre.next;
return node;
}
}
@Override
public void sort(Comparable[] a) {
LinkList linkList = creLLR(a);
ListNode<Comparable> pre = linkList.head, node = pre.next, mid = pre;
int flag = 0;
while (node != null) {
if (Common.less(node.data, pre.data)) {
if (flag == 1) pre = merge(linkList, linkList.head, mid, pre);
mid = pre;
pre = pre.next;
flag = 1;
} else pre = pre.next;
node = pre.next;
}
if (a.length > 1 && Common.less((Comparable) mid.next.data, mid.data))
merge(linkList, linkList.head, mid, pre);
}
}
*2.2.18 未解决
题目
*打乱链表。*实现一个分治算法,使用线性对数级别的时间和对数级别的额外空间随机打乱一条链表。
评估
代码实现
2.2.19
题目
*倒置。*编写一个线性对数级别的算法统计给定数组中的"倒置"数量(即插入排序所需的交换次数,请见2.1节)。这个数量和Kendall tau距离有关,请见2.5节。
评估
我是利用自底向上的归并方法统计次数,自顶向下也可
主要其实就是统计 此时满足 编写一个线性对数级别的算法统计给定数组中的"倒置"数量(即插入排序所需的交换次数,请见2.1节)。 这个数量和Kendall tau距离有关,请见2.5节。
*
* @author cyy
*/ *间接排序。*编写一个不改变数组的归并排序,它返回一个int[]数组perm,其中perm[i]的值是原数组中第i小的元素的位置。 用辅助数组 之前是对 所以在 编写一个不改变数组的归并排序,它返回一个int[]数组perm,其中perm[i]的值是原数组中第i小的元素的位置。
*
* @author cyy
*/ *一式三份。*给定三个列表,每个列表中包含N个名字,编写一个线性对数级别的算法来判定三份列表中是否含有公共的名字,如果有,返回第一个被找到了这种名字。 给定三个列表,每个列表中包含N个名字,编写一个线性对数级别的算法来判定三份列表中是否含有公共的名字,如果有,返回第一个被找到了这种名字。
*
* @author cyy
*/ *三向归并排序。*假设每次我们是把数组分成三个部分而不是两个部分并将它们分别排序,然后进行三向归并。这种算法的运行时间的增长数量级是多少? 先讨论三元素的数组在进行merge时所需要进行比较的次数,参考书本命题I的比较树我们可以知道,要获得三个元素中最小的值,需要进行2次比较,若有数组已经遍历完,则只需一次比较。 假设该三叉树(?)共有n层,即3n=N 则在第k层(0≤k≤n-1),数组长度为3n-k,需要进行2×3n-k次比较, 每层有3k个数组,因此每层需要进行 3k × 2×3n-k = 2×3n 次比较, 因为共有n层,因此总共需要n×2×3n = 2n3n次比较 因此,三向归并排序算法的运行时间的增长数量级是O(Nlog3N)。 假设每次我们是把数组分成三个部分而不是两个部分并将它们分别排序,然后进行三向归并。这种算法的运行时间的增长数量级是多少?
*
* @author cyy
*/ 改进。用实验评估正文中所提到的归并排序的三项改进(请见练习2.2.11)的效果,并比较正文中实现的归并和练习2.2.10所实现的归并之间的性能。根据经验给出应该在何时为子数组切换到插入排序。 用实验评估正文中所提到的归并排序的三项改进(请见练习2.2.11)的效果,
*
* 并比较正文中实现的归并和练习2.2.10所实现的归并之间的性能。
*
* 根据经验给出应该在何时为子数组切换到插入排序。
*
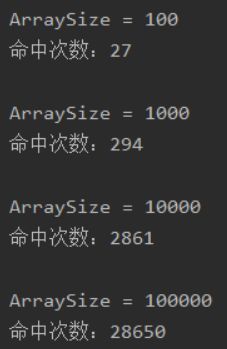
* @author cyy
*/ *改进的有序测试。*在实现中用大型随机数组评估练习2.2.8所做的修改的效果。根据经验用N(被排序的原始数组的大小)的函数描述条件语句(a[mid]<=a[mid+1])成立(无论数组是否有序)的平均次数。 *多向归并排序。*实现一个k向(相对双向而言)归并排序程序。分析你的算法,估计最佳的k值并通过实验验证猜想。 *创建数组。*使用SortCompare粗略比较在你的计算机上在merge()中和在sort()中创建aux[]的性能差异。 使用SortCompare粗略比较在你的计算机上在merge()中和在sort()中创建aux[]的性能差异。
*
* @author cyy
*/ *子数组长度。*用归并将大型随机数组排序,根据经验用N(某次归并时两个子数组的长度之和)的函数估计当一个子数组用尽时另一个子数组的平均长度。 平均围绕在1,也就是说排序下来,每次归并同一长度为N(某次归并时两个子数组的长度之和)的子数组时,平均下来很少出现顺序、倒序情况,两个子数组中的数值基于交叉存在。 用归并将大型随机数组排序,根据经验用N(某次归并时两个子数组的长度之和)的函数估计当一个子数组用尽时另一个子数组的平均长度。
*
* @author cyy
*/ *自顶向下与自底向上。*对于N=103、104、105和106,使用SortCompare比较自顶向下和自底向上的归并排序的性能。 对于N=10^3、10^4、10^5和10^6,使用SortCompare比较自顶向下和自底向上的归并排序的性能。
*
* @author cyy
*/ *自然的归并排序。*对于N=103、106和109,类型为Long的随机主键数组,根据经验给出自然的归并排序(请见练习2.2.16)所需要的遍数。提示:不需要实现这个排序(甚至不需要生成所有完整的64位主键)也能完成这道练习。 因此平均需要 N/2 次 https://home.cnblogs.com/u/longjin2018/ https://www.cnblogs.com/ikesnowy/p/9258128.htmlless(a[j],a[i])的次数,需要注意的是每一次的 a[j]less(a[j],a[i]),但是对应的倒置个数应该是 mid - i + 1 ,意味着 a[j] < a[i+1…] 也满足代码实现
/**
* 倒置。
*
* 2.2.20
题目
解答
int[] aux来作为排序对象数组 a的下标记录。a进行排序,现在直接对 perm进行排序,只是通过修改 aux即 a的下标 来记录数组的排序。merge方法中进行比较要使用 less(a[aux[j]], a[aux[i]])代码实现
/**
* 间接排序。
*
* 2.2.21
题目
解答
代码实现
/**
* 一式三份。
*
* 2.2.22
题目
分析
代码实现
/**
* 三向归并排序。
*
* 2.2.23
题目
评估
代码实现
/**
* 改进。
*
* 2.2.24
题目
评估
代码实现
public class ex8 implements BaseSort {
private static Comparable[] aux;
private static int ctime;
private static int count;
public static void main(String[] args) {
// 2.2.24
for (int n = 100; n <= 100000; n *= 10) {
count = 0;
for (int i = 0; i < 10; i++) {
new ex8().sort(ArrayGenerate.random(n));
}
System.out.println("\nArraySize = " + n + "\n命中次数:" + count / 10);
}
}
private static void sort(Comparable[] a, int l, int r) {
ctime++;
if (l >= r) return;
int mid = (l + r) / 2;
sort(a, l, mid);
sort(a, mid + 1, r);
if (Common.less(a[mid], a[mid + 1])) {
count++;
return;
}
merge(a, l, mid, r);
}
private static void merge(Comparable[] a, int l, int mid, int r) {
int i = l, j = mid + 1;
ctime++;
System.arraycopy(a, l, aux, l, r - l + 1);
for (int k = l; k <= r; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > r) a[k] = aux[i++];
else if (Common.less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
@Override
public void sort(Comparable[] a) {
aux = a.clone();
sort(a, 0, a.length - 1);
}
}
*2.2.25 未解决
题目
评估
代码实现
2.2.26
题目
评估
代码实现
/**
* 创建数组。
*
* 2.2.27
题目
评估

代码实现
/**
* 子数组长度。
*
* 2.2.28
题目
评估
代码实现
/**
* 自顶向下与自底向上。
*
* 2.2.29
题目
评估
Common.less(a[i], a[i - 1]),所以只需0次参考