数字图像处理第五章 几何变换与图像配准

几何变换与图像配准

几何变换改变了图像中像素间的空间关系，可以用于创建小场景，使之适应从某个重放分辨率到另一个分辨率的数字视频，校正由观察几何变换导致的失真，以及排列有相同场景和目标的多幅图像。这一章，我们研究图像几何变换的主要概念，以图像配准和为了定量比较对准有相同场景和目标的多幅图像的处理来结束本章。

1 点变换

假设(w,z)和(x,y)是两个空间坐标系统，分别称为输入空间和输出空间。几何坐标变换可定义为输入空间点到输出空间点的映射:$$(x,y)=T\{(w,z)\}$$这里，T{·}叫做正向变换或正向映射。如果T{·}有逆，可逆映射输出空间点到输入空间点:$$(w,z)=T^{-1}\{(x,y)\}$$这里，T^-1{·}叫做逆变换或逆映射。

下面我们用个实际例子来演示一下，第一个变换用因数3水平放大，用因数2垂直放大:

>> forward_fcn = @(wz, tdata) [3*wz(:,1),2*wz(:,2)]

forward_fcn = 

    @(wz,tdata)[3*wz(:,1),2*wz(:,2)]

>> inverse_fcn = @(xy, tdata) [xy(:,1)/3,xy(:,2)/2]

inverse_fcn = 

    @(xy,tdata)[xy(:,1)/3,xy(:,2)/2]

>> tform1 = maketform('custom', 2, 2, forward_fcn, inverse_fcn, [])

tform1 = 

       ndims_in: 2
      ndims_out: 2
    forward_fcn: @(wz,tdata)[3*wz(:,1),2*wz(:,2)]
    inverse_fcn: @(xy,tdata)[xy(:,1)/3,xy(:,2)/2]
          tdata: []
>> WZ = [1 1; 3 2];
>> XY = tformfwd(WZ, tform1)

XY =

     3     2
     9     4

>> WZ2 = tforminv(XY, tform1)

WZ2 =

     1     1
     3     2

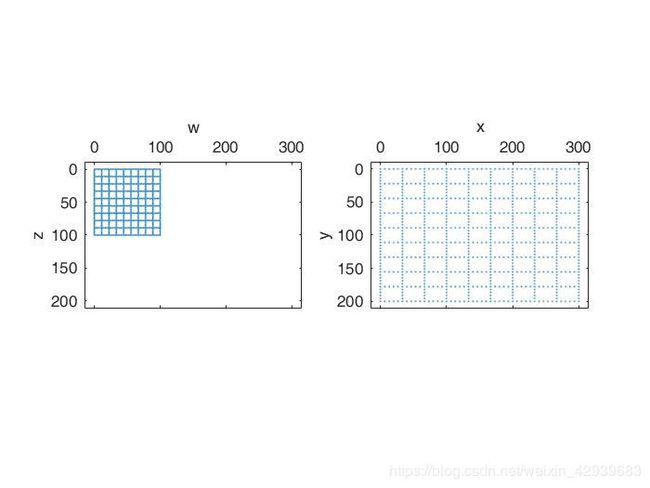
为了能对特殊的空间变换有一个较好的感觉，下面自定义两个M-函数pointgrid和vistform可帮助目测检验给定的变换。

function wz = pointgrid( corners )

[w1, z1] = meshgrid(linspace(corners(1,1), corners(2,1), 46), linspace(corners(1), corners(2), 10));

[w2, z2] = meshgrid(linspace(corners(1), corners(2), 10), linspace(corners(1), corners(2), 46));

wz = [w1(:) z1(:); w2(:) z2(:)];
end

function vistform(tform, wz )

xy = tformfwd(tform, wz);

minlim = min([wz; xy], [], 1);
maxlim = max([wz; xy], [], 1);

bump = max((maxlim - minlim) * 0.05, 0.1);
limits = [minlim(1) - bump(1), maxlim(1) + bump(1), minlim(2) - bump(2), maxlim(2) + bump(2)];

subplot(1,2,1)
grid_plot(wz, limits, 'w', 'z')
subplot(1,2,2)
grid_plot(xy, limits, 'x', 'y')
end

function grid_plot( ab, limits, a_label, b_label )

plot(ab(:,1), ab(:,2), '.', 'MarkerSize', 2)
axis equal, axis ij, axis(limits);
set(gca, 'XAxisLocation', 'top')
xlabel(a_label), ylabel(b_label)

end

>> vistform(tform1, pointgrid([0 0; 100 100]))

2 仿射变换

对于2D变换，仿射变换可写成下式：
$$\left[\begin{array}{cc}x& y\end{array}\right]=\left[\begin{array}{cc}w& z\end{array}\right]\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]+\left[\begin{array}{cc}{b}_1& b_2\end{array}\right]$$
为了数学和计算方便，仿射变换可用附加第三坐标的方法写成矩阵相乘形式：
$$\left[\begin{array}{ccc}x& y& 1\end{array}\right]=\left[\begin{array}{ccc}w& z& 1\end{array}\right]\left[\begin{array}{ccc}{a}_{11}& a_{12}& 0\\ a_{21}& a_{22}& 0\\ b_1& b_2& 1\end{array}\right]$$

>> T = [1 0 0 ; 0.4 1 0 ; 0 0 1];
>> tform3 = maketform('affine', T);
>> WZ

WZ =

     1     1
     3     2

>> XY1 = tformfwd(WZ, tform3)

XY1 =

    1.4000    1.0000
    3.8000    2.0000

这里我们设置的是一个简单的水平裁剪的仿射矩阵，仿射矩阵有很多种，会根据不同需要来使用，下面是几个常用的仿射矩阵。

3 投影变换

另一种有用的几何变换类型是投影变换，包括在空间情况下的仿射变换的投影变换在一幅图像的逆透视图变换中是很有用的。正如仿射变换那样，这对使用辅助第三维定义二维投影变换很有用。然而，与仿射变换不同，辅助坐标（下式中的h）不是常量。
$$\left[\begin{array}{ccc}{x}^{{}^{\prime }}& y^{{}^{\prime }}& h\end{array}\right]=\left[\begin{array}{ccc}w& z& 1\end{array}\right]\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ b_1& b_2& 1\end{array}\right]$$

>> T = [-2.7390 0.2929 -0.6373
0.7426 -0.7500 0.8088
2.8750 0.7500 1.0000];
>> tform = maketform('projective', T);
>> vistform(tform, pointgrid([0 0 ; 1 1]));

下面是投影变换的效果：

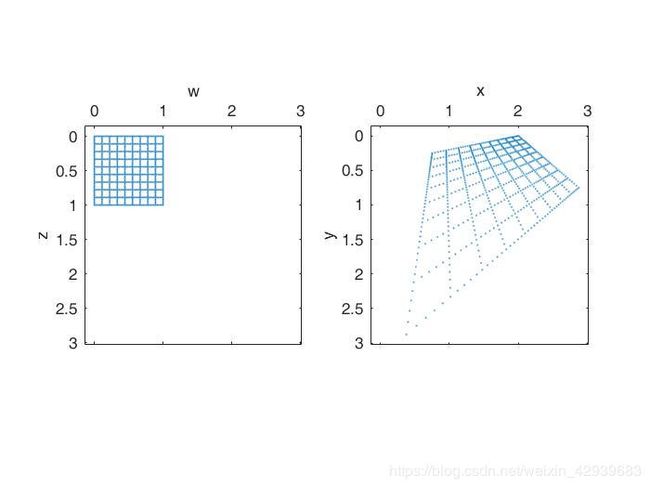
下图说明了上图中投影变换的某些几何特性，上图中输入空间网格中有两组平行线，一组是水平的，一组是垂直的。下图显示了两组平行线变换到输出空间后的线，在称为尽头点的位置交叉。尽头点位于地平线上，当变换的时候，仅平行于水平线的输入空间的线保持水平，所有其他平行线变换为在位于地平线上尽头点处交叉的线。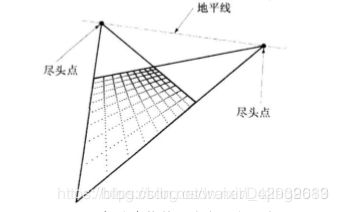

4 应用于图像的几何变换

我们已经学习了如何把几何变换应用于点，下面将进一步考虑如何把几何变换应用于图像。我们使用图像处理工具箱中的imtransform函数作用于图像：

>> f = checkerboard(50);
>> sx = 0.75;
>> sy = 1.25;
>> T = [sx 0 0
0 sy 0
0 0  1];
>> t1 = maketform('affine', T);
>> g1 = imtransform(f, t1);
>> imshow(g1,[])
>> theta = pi/6;
>> T2 = [cos(theta) sin(theta) 0
-sin(theta) cos(theta) 0
0           0          1];
>> t2 = maketform('affine', T2);
>> g2 = imtransform(f, t2);
>> imshow(g2,[])
>> T3 = [0.4788 0.0135 -0.0009
0.0135 0.4788 -0.0009
0.5059 0.5059 1.0000];
>> t3 = maketform('projective', T3);
>> g3 = imtransform(f, t3);
>> subplot(2,2,1),imshow(f,[]),title('Orginal Image');
>> subplot(2,2,2),imshow(g1,[]),title('Scale Transform Image');
>> subplot(2,2,3),imshow(g2,[]),title('Rotation Transform Image');
>> subplot(2,2,4),imshow(g3,[]),title('Projective Transform Image');

5 MATLAB中的图像坐标系统

5.1 输出图像位置
在之前的仿射变换中输出图像并没有显示在输出空间中图像的位置。函数imtransform可以通过使用附加参数来提供这个信息，其中XData特性是两向量元素，其中，第一个元素指定像素第一列中心的x坐标，第二个元素指定像素最后一列中心的x坐标。类似的，YData的两个元素指定了第一行和最后一行中心的y坐标，对于包含M行、N列的图像来说，默认的XData向量是[1,N]，默认的YData向量是[1,M]：

>> f = imread('dog2.jpg');
>> imshow(f)
>> iptsetpref imshowAxesVisible on
>> axis on
>> xlabel x
>> ylabel y
>> hold on
>> theta = 3 * pi /4;
>> T = [cos(theta) sin(theta) 0
-sin(theta) cos(theta) 0
0           0          1];
>> tform = maketform('affine', T);
>> [g,xdata,ydata]=imtransform(f,tform,'FillValue',255);
>> imshow(g,'XData',xdata,'YData',ydata)
>> axis auto

5.2 控制输出网格
前面说明了如何用 xdata 和 ydata 参数形象化平移的效果，从输出 imtransform 到输 入 imshow。另一个方法是在输出空间中用imtransform 直接控制像素网格。通常，imtransform 在输出空间中用下列步骤定位和计算输出图像：
(1) 决定输入图像的边界矩形。
(2) 在边界矩形上把点变换到输出空间中。
(3) 计算变换后输出空间中点的边界矩形。
(4) 计算位于输出空间中、边界矩形内的网格上的输出图像像素。
下面我们引入M-函数imtransform2来输出图像：

function g=imtransform2(f,varargin)
[M,N]=size(f);
xdata=[1 N];
ydata=[1 M];
g=imtransform(f,varargin{:},'XData',xdata,'YData',ydata);

>> f = imread('dog2.jpg');
>> tform1=maketform('affine',[1 0 0;0 1 0;300 500 1]);
>> g1=imtransform2(f,tform1,'FillValue',200);
>> h1=imtransform(f,tform1,'FillValue',200);
>> tform2=maketform('affine',[0.25 0 0;0 0.25 0;0 0 1]);
>> g2=imtransform2(f,tform2,'FillValues',200);
>> h2=imtransform(f,tform2,'FillValues',200);
>> subplot(1, 3, 1),imshow(f);title('Original Image');
>> subplot(1, 3, 2),imshow(g1);title('Transfer By imtransform2');
>> subplot(1, 3, 3),imshow(h1);title('Transfer By imtransform');
>> subplot(1, 2, 1),imshow(g2);title('Transfer By imtransform2');
>> subplot(1, 2, 2),imshow(h2);title('Transfer By imtransform');

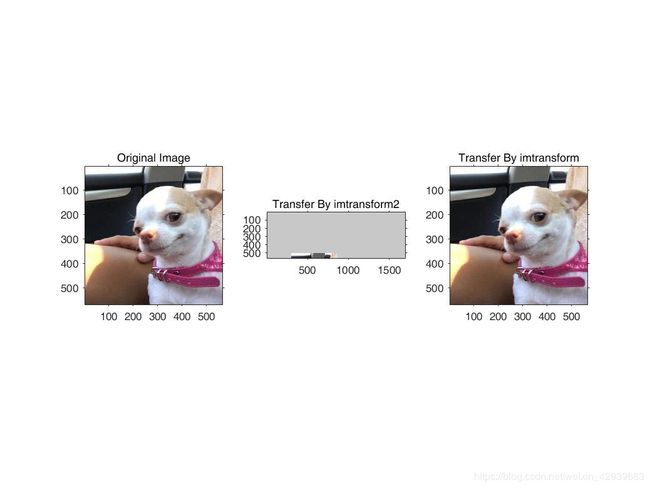
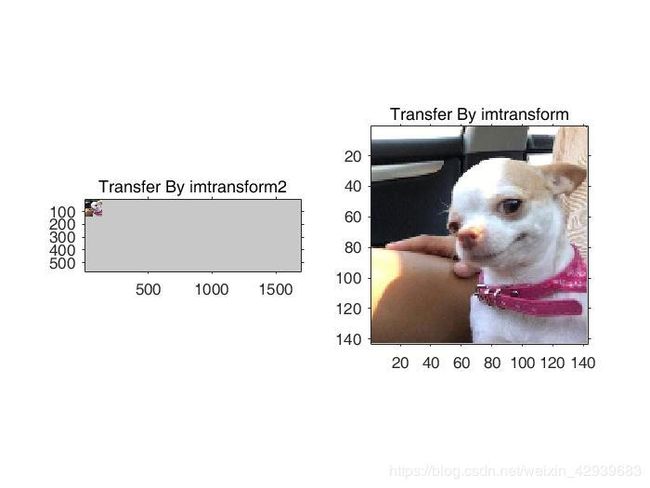
从上面两张图可以看出使用imtransform2 的结果，与imtransform进行比较，可以很容易地 看出平移的效果。第一张图imtransform2 的结果，输出图像的一部分已被切掉，而在imtransform 的结果中，全部输出图像是可见的，但是失去了平移效果。第二张图两个输出显示了全部输出图像。从 imtransform2 的输出可以看到，虽然比变换后的图像大，但填充的像素灰度很协调，而来自函数 imtransform 的输出刚好包含变换后的图像。

5 图像内插

对于数字图像，f的值仅在整数值位置的知道的。使用这些已知的值去估计在非整数值位置的f是内插的典型示例——用离散数据构建连续定义的函数。内插具有很长的历史，很多年来，已经提出了众多的内插方法。在信号处理文献中，内插常常被解释为拥有两个设计步骤的重采样过程：
（1）把连续变换离散化，把拥有连续域定义的函数f^’转换为在离散域定义的函数f。
（2）在离散位置估计f^’的值。
这里我们介绍两种基本的内插方法。

5.1 最近邻差值法
顾名思义，最近邻内插法就是选取距离内插像素最近的像素点，以一定的规则选取像素值作为内插的像素值。

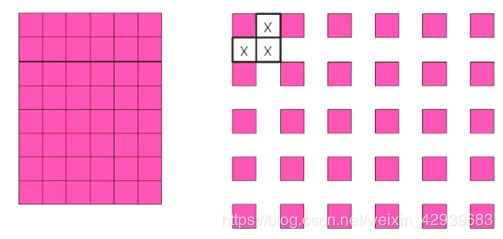
虽然的算法复杂度最低的内插方法，但是放大图像很容易产生马赛克效果，视觉上的效果也是最差的。

5.2 双线性差值
双线性插值是对最近邻的一种改进，即用线性内插方法，根据点的四个相邻点的灰度值，分别在和方向上进行两次插值，计算新值。


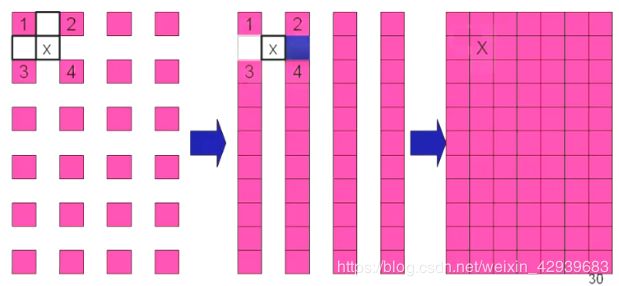
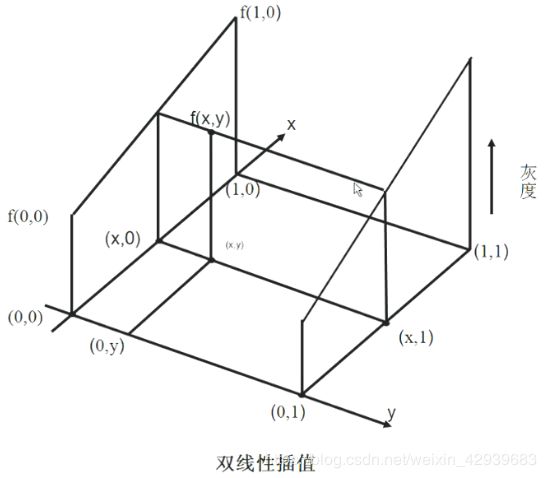
首先，在x方向上做线性插值，对上端的两个顶尖进行线性插值的：$$f(x,0)=f(0,0)+x[f(1,0)-f(0,0)]$$类似的，对于底端两个顶点进行线性插值有：$$f(x,1)=f(0,1)+x[f(1,1)-f(0,1)]$$y方向上做线性插值，以确定：$$f(x,y)=f(x,1)+y[f(x,1)-f(x,0)]$$最后得到双线性插值公式为：$$f(x,y)=[f(1,0)-f(0,0)]x+[f(0,1)-f(0,0)]y+[f(1,1)+f(0,0)-f(0,1)-f(1,0)]xy+f(0,0)$$上述两种方法都不是适用于真正图像处理内插时的最佳方法，效果越好的内插方法越会考虑内插像素周围更多的像素点的值并且加入了每个像素的权值，这里就不一一介绍了。

6 图像配准

几何变换最重要的图像处理应用之一是图像配准。图像配准方法寻求对两幅或多幅相同场景的图像。在同时获取多幅图像的时，会有不同的情节发生，但采用不同的手段。例如，为了测量场景深度，在不同位置的两台摄像机可能同时获取相同的场景同时发生的图像。图像配准方法通常由下列步骤组成：
（1）检测特征
（2）匹配相应特征
（3）推断几何变换
（4）通过几何变换用另一幅图像对准一幅图像
图像配准方法可以是手工的或自动的，这取决于特征检测和配准是由人辅助的还是用自动算法执行。

6.1基于区域的配准
对于外在特征选择和匹配的可供选择的方法是基于区域的配准。在基于区域的配准中，称做模板图像的一幅图像被移动以覆盖第二张图像的每个位置。在每个位置，计算基于区域的相似性度量。如果在相似性度量中，在某个特定位置找到明显的峰值，就可以说模板图像在第二幅图像的某个特定位置匹配。

对于基于区域的配准来说，使用的相似性度量是归一化互相关（也叫相关系数）。图像和模板之间的归一化互相关的定义是：$$\gamma (x,y)=\frac{{\sum }_{s,t}[w(s,t)-\bar{w}][f(x+s,y+t)-\overline{f_{xy}}]}{\sqrt{{\sum }_{s,t}[w(s,t)-\bar{w}{]}^2{\sum }_{s,t}[f(x+s,y+t)-\overline{f_{xy}}{]}^2}}$$其中，w是模板，wbar是模板像素的平均值，f是图像，fbar是w和f覆盖的那个区域图像的平均值。

>> f = rgb2gray(imread('mona_target.jpg'));
>> w = rgb2gray(imread('mona_source.png'));
>> g = normxcorr2(w,f);
>> subplot(1, 3, 1), imshow(f);title('Original Image');
>> subplot(1, 3, 2), imshow(w);title('Template Image');
>> subplot(1, 3, 3), imshow(abs(g));title('Normalized Absolute Value');

图像配准的优秀算法很多，并且成熟的算法也很多，这里仅仅只是最基础的方法，感兴趣的话就要深入这个领域了。