四种常用聚类及代码(一):K-Means
K-Means
- K-Means
- K-Means算法:
- K-Means缺点:
- K-Means优化:
- 评价方法-轮廓系数
- K-Means实现
K-Means
K-Means是最为经典的无监督聚类(Unsupervised Clustering)算法,其主要目的是将n个样本点划分为k个簇,使得相似的样本尽量被分到同一个聚簇。K-Means衡量相似度的计算方法为欧氏距离(Euclid Distance)。
K-Means算法的特点是类别的个数是人为给定的,如果让机器自己去找类别的个数,我们有AP聚类算法。K-Means的一个重要的假设是:数据之间的相似度可以使用欧氏距离度量,如果不能使用欧氏距离度量,要先把数据转换到能用欧氏距离度量,这一点很重要。(注:可以使用欧氏距离度量的意思就是欧氏距离越小,两个数据相似度越高)
K-Means算法:
伪代码如下:
function K-Means(输入数据,中心点个数K)
获取输入数据的维度Dim和个数N
随机生成K个Dim维的点,或随机选k个样本中的点
while(算法未收敛)
对N个点:计算每个点属于哪一类。
对于K个中心点:
1,找出所有属于自己这一类的所有数据点
2,把自己的坐标修改为这些数据点的中心点坐标,即平均值
end
输出结果:
end
数据集 D有 N个样本点 {x1,x2,…,xn},假设现在要将这些样本点聚类为 k个簇, k个簇中心为{μ1,μ2,…,μn } 。定义指示变量 γij ∈ \in ∈{0,1},如果第 i个样本被聚类到第 k个簇,那么 γij=1,否则 γij=0 。在K-Means中每个样本只能属于一个簇,这是Hard-Clustering,也称为Non-fuzzy Clustering,与之对应的是Soft-Clustering或者Fuzzy-Clustering,指的是一个样本可以被归为多个簇。在K-Means里面有 ∑ \sum ∑j γij=1,那么K-Means的优化目标为:
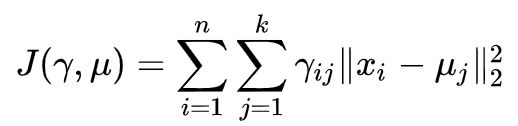
目标需要优化的变量有 和 ,由于 是01离散变量,优化起来是NP-Hard问题。所以采用启发式的求解,即Lloyd’s algorithm。求解过程分为Assignment和Update两步。
Assignment Step:
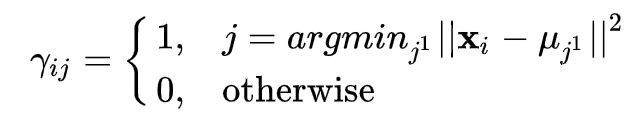
Update Step:

在Assignment Step,把样本归为最近的簇中心所代表的簇,很明显,这一步更新会减小目标函数的值;在Update Step中,更新聚簇中心,用这个簇的所有样本的中心点当作新的聚簇中心,不难证明这一步是最小化簇内样本到聚簇中心欧式距离平方和的最优解。所以,按照上述两步,只要有 和 被更新了,那么目标函数值肯定会下降。由于将 个样本点分配到 个聚簇中心最多只有 个划分方案,每一种划分方案对应一个目标函数值。采用上述两步算法,每步更新都会使得目标函数值减少,故上述算法流程肯定会收敛。但是由于是采用的启发式算法,不一定能保证收敛到全局最优解。事实上,K-Means的两步更新可以看作是EM算法的两步,即Expectation和Maximization两步,这里不再详细介绍。
K-Means缺点:
1、需要确定K的值。K的取值需要事先确定,然而在无监督聚类任务上,由于并不知道数据集究竟有多少类别,所以很难确定K的取值。举例来说,利用K-Means做 彩色图像分割(Segmentation)任务,如果图像只有一个物体和背景,那么很容易确定将K设置为2,并且较容易得到比较好的分割效果,但是对于一副有更多物体的图像,K的设定就很难了,因为我们并不总能人工去判断这幅图像里面有几个类别。对于文档聚类更是如此,比如一批新闻 数据集,可以按照主题聚类,但是有多少主题呢,这个不能事先获得。
2、对异常点敏感。K-Means很容易受到异常点(outliers)的影响,由于K-Means在Update Step取得是簇内样本均值,那么就会很容易受到异常点的影响,比如某个簇内样本在某个维度上的值特别大,这就使得聚簇中心偏向于异常点,从而导致不太好的聚类效果。
3、凸形聚类。K-Means由于采用欧氏距离来衡量样本之间相似度,所以得到的聚簇都是凸的,就不能解决“S型”数据分布的聚类,这就使得K-Means的应用范围受限,难以发现数据集中一些非凸的性质。
4、聚簇中心初始化,收敛到局部最优,未考虑密度分布等等。
K-Means优化:
K-Medians。不同于K-Means使用欧式距离计算目标函数,K-Medians使用曼哈顿距离(Manhattan Distance),对应的则是 l1范数。在目标求解的Update过程中,用簇内样本每个维度的中位数来当作聚簇中心在该维度的值(K-Means使用的是平均值),K-Medians的Median就是这个意思;在Assignment过程中,使用曼哈顿距离将每个样本划归为最近的聚簇。K-Medians可以很好地解决异常点问题.不难发现,在异常点的影响下,K-Medians更鲁棒,能较好的代表聚类结果。
K-Medoids。在K-Means中,聚簇中心不一定是样本点,而是样本点的中心。但是在K-Medoids中,聚簇中心就是样本点。比如在初始化过程中,K-Means是随机初始化k个聚簇中心,K-Medoids是在样本集中选择k个作为聚簇中心。即便K-Means初始过程中也可以选择样本点,但是在后续Step中,K-Medoids一直保持聚簇中心为样本点,K-Means则不然。另外,K-Medoids使用的是和K-Medians一样的曼哈顿距离,更新聚簇中心时,在簇内选择一个使得簇内曼哈顿距离之和最小的样本点作为聚簇中心。选择样本点作为聚簇中心的一个好处是聚簇中心可能是稀疏的,比如在文本聚类中,文本向量大多数是稀疏向量,系数向量计算相似度或距离速度更快。
K-Means++。初始聚簇中心的选择是K-Means的一个重要难点,K-Means++使用了一种方法来寻找到一组比较好的初始聚簇中心。其主要思想是:首先,选择一个样本点作为第一个聚簇中心,然后再选择下一个聚簇中心时要尽量离第一个已经选择的簇中心远一些,选择的方法是根据一个概率分布,这个概率分布和样本到聚簇中心的距离有关,比如 ,即已选择的聚簇中心越远概率越大;对于第三个聚簇中心的选择,需要加权考虑到第一、第二个已选择聚簇中心的距离。重复上述过程直到选出k个聚簇中心。K-Means++可以很好地解决K-Means的初始化问题。
其他聚类方法。为了解决K-Means的K初始值选取的问题,可以采用层次聚类(Hierarchical Clustering)的方法;为了解决K-Means未考虑密度分布以及非凸聚类的缺陷,可以考虑使用密度聚类DBSCAN算法。此外还有很多聚类算法,比如混合高斯聚类。
评价方法-轮廓系数
这里提一下聚类算法中最常用的评估方法——轮廓系数(Silhouette Coefficient):
计算样本i到同簇其它样本到平均距离ai。ai越小,说明样本i越应该被聚类到该簇(将ai称为样本i到簇内不相似度)。
计算样本i到其它某簇Cj的所有样本的平均距离bij,称为样本i与簇Cj的不相似度。定义为样本i的簇间不相似度: b i = m i n ( b i 1 , b i 2 , . . . , b i k 2 ) b_i=min(b_{i1},b_{i2},...,b_{ik2}) bi=min(bi1,bi2,...,bik2)
si接近1,则说明样本i聚类合理
si接近-1,则说明样本i更应该分类到另外的簇
若si近似为0,则说明样本i在两个簇的边界上
K-Means实现
from numpy import *
import time
import matplotlib.pyplot as plt
# calculate Euclidean distance
def euclDistance(vector1, vector2):
return sqrt(sum(power(vector2 - vector1, 2)))
# init centroids with random samples
def initCentroids(dataSet, k):
numSamples, dim = dataSet.shape
centroids = zeros((k, dim))
for i in range(k):
index = int(random.uniform(0, numSamples))
centroids[i, :] = dataSet[index, :]
return centroids
# k-means cluster
def kmeans(dataSet, k):
numSamples = dataSet.shape[0]
# first column stores which cluster this sample belongs to,
# second column stores the error between this sample and its centroid
clusterAssment = mat(zeros((numSamples, 2)))
clusterChanged = True
## step 1: init centroids
centroids = initCentroids(dataSet, k)
while clusterChanged:
clusterChanged = False
## for each sample
for i in xrange(numSamples):
minDist = 100000.0
minIndex = 0
## for each centroid
## step 2: find the centroid who is closest
for j in range(k):
distance = euclDistance(centroids[j, :], dataSet[i, :])
if distance < minDist:
minDist = distance
minIndex = j
## step 3: update its cluster
if clusterAssment[i, 0] != minIndex:
clusterChanged = True
clusterAssment[i, :] = minIndex, minDist**2
## step 4: update centroids
for j in range(k):
pointsInCluster = dataSet[nonzero(clusterAssment[:, 0].A == j)[0]]
centroids[j, :] = mean(pointsInCluster, axis = 0)
print 'Congratulations, cluster complete!'
return centroids, clusterAssment
# show your cluster only available with 2-D data
def showCluster(dataSet, k, centroids, clusterAssment):
numSamples, dim = dataSet.shape
if dim != 2:
print "Sorry! I can not draw because the dimension of your data is not 2!"
return 1
mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ', 'pr']
if k > len(mark):
print "Sorry! Your k is too large! please contact Zouxy"
return 1
# draw all samples
for i in xrange(numSamples):
markIndex = int(clusterAssment[i, 0])
plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex])
mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', ', 'pb']
# draw the centroids
for i in range(k):
plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize = 12)
plt.show()
#测试代码:
from numpy import *
import time
import matplotlib.pyplot as plt
## step 1: load data
print "step 1: load data..."
dataSet = []
fileIn = open('E:/Python/Machine Learning in Action/testSet.txt')
for line in fileIn.readlines():
lineArr = line.strip().split('\t')
dataSet.append([float(lineArr[0]), float(lineArr[1])])
## step 2: clustering...
print "step 2: clustering..."
dataSet = mat(dataSet)
k = 4
centroids, clusterAssment = kmeans(dataSet, k)
## step 3: show the result
print "step 3: show the result..."
showCluster(dataSet, k, centroids, clusterAssment)
c++实现:
#include
#include
#include 