算法与数据结构复习 第二章 线性表(详解)

第二章 线性表

书面作业

一、判断题

1、顺序存储的线性表可以随机存取。(T)

解析：
线性表的顺序存储结构可以通过线性表的首址加偏移的方法计算出来第i个数据的位置；而线性表的链式存储结构要访问第i个数据,就必须先访问前面的i-1个数据；

2、在具有N个结点的单链表中，访问结点和增加结点的时间复杂度分别对应为O(1)和O(N)。 (F)

解析：
访问结点和增加结点的时间复杂度分别对应为O(N)和O(1)；

3、线性表采用链式存储表示时，所有结点之间的存储单元地址可以连续也可以不连续。 (T)

4、顺序表 - 存储结构

​ 顺序表中逻辑上相邻的元素，其物理位置一定相邻。(T)

5、带头结点的单循环链表中，任一结点的后继结点的指针域均不空。 (T)

6、在单向链表中，头指针中存放的是头结点的内容。 (F)

解析：

头指针中存放的是头结点的地址

7、对于顺序存储的长度为N的线性表，访问结点和增加结点的时间复杂度分别对应为O(1)和O(N)。 (T)

8、循环链表可以做到从任一结点出发，访问到链表的全部结点。 (T)

9、线性表的唯一存储形式是链表。 (F)

10、若用链表来表示一个线性表，则表中元素的地址一定是连续的。 (F)

11、若某线性表最常用的操作是存取任一指定序号的元素和在最后进行插入和删除运算，则利用顺序表存储最节省时间。 (T)

12、单链表中引入头结点会使结点插入操作的时间复杂度降为常数阶。 (F)

13、通常使用结构的嵌套来定义单向链表结点的数据类型。 (T)

二、单选题

1、能在O(1)时间内访问线性表的第i个元素的结构是（A）。

1. 顺序表
2. 单链表
3. 单向循环链表
4. 双向链表
5. 替换为错误项

2、若某线性表最常用的操作是存取任一指定序号的元素和在最后进行插入和删除运算，则利用哪种存储方式最节省时间？ (D)

1. 双链表
2. 单循环链表
3. 带头结点的双循环链表
4. 顺序表

3、在单链表中，若p所指的结点不是最后结点，在p之后插入s所指结点，则执行 (C )

1. s->next=p; p->next=s;
2. s->next=p->next; p=s;
3. s->next=p->next; p->next=s;
4. p->next=s; s->next=p;

4、已知L是带头结点的单链表，则摘除首元结点的语句是（B）。

1. L=L->link;
2. L->link=L->link->link;
3. L=L->link->link;
4. L->link = L；

5、链表不具有的特点是： (B)

1. 插入、删除不需要移动元素
2. 方便随机访问任一元素
3. 不必事先估计存储空间
4. 所需空间与线性长度成正比

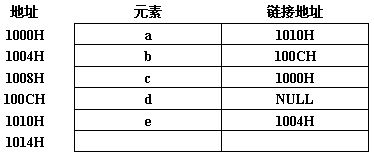
6、已知表头元素为c的单链表在内存中的存储状态如下表所示：

现将f存放于1014H处，并插入到单链表中，若f在逻辑上位于a和e之间，则a、e、f的“链接地址”依次

是：(D)

1. 1010H, 1014H, 1004H
2. 1010H, 1004H, 1014H
3. 1014H, 1010H, 1004H
4. 1014H, 1004H, 1010H

7、对于一个具有N个结点的单链表，在给定值为x的结点后插入一个新结点的时间复杂度为 (C )

1. O(1)
2. O(N/2)
3. O(N)
4. O($N^2$)

8、某线性表中最常用的操作是在最后一个元素之后插入一个元素和删除第一个元素，则采用什么存储方式最节省运算时间？ (B)

1. 单链表
2. 仅有尾指针的单循环链表
3. 仅有头指针的单循环链表
4. 双链表

9、将线性表La和Lb头尾连接，要求时间复杂度为O(1)，且占用辅助空间尽量小。应该使用哪种结构？ ©

1. 单链表
2. 单循环链表
3. 带尾指针的单循环链表
4. 带头结点的双循环链表

10、在N个结点的顺序表中，算法的时间复杂度为O(1)的操作是：(A)

1. 访问第i个结点（1≤i≤N）和求第i个结点的直接前驱（2≤i≤N）
2. 在第i个结点后插入一个新结点（1≤i≤N）
3. 删除第i个结点（1≤i≤N）
4. 将N个结点从小到大排序

11、在双向循环链表结点p之后插入s的语句是： (D)

1. p->next=s; s->prior=p; p->next->prior=s ; s->next=p->next;
2. p->next->prior=s; p->next=s; s->prior=p; s->next=p->next;
3. s->prior=p; s->next=p->next; p->next=s; p->next->prior=s;
4. s->prior=p; s->next=p->next; p->next->prior=s; p->next=s;

12、在双向链表存储结构中，删除p所指的结点，相应语句为：©

1. p->prior=p->prior->prior; p->prior->next=p;
2. p->next->prior=p; p->next=p->next->next;
3. p->prior->next=p->next; p->next->prior=p->prior;
4. p->next=p->prior->prior; p->prior=p->next->next;

13、设h为不带头结点的单向链表。在h的头上插入一个新结点t的语句是：(D)

1. h=t; t->next=h->next;
2. t->next=h->next; h=t;
3. h=t; t->next=h;
4. t->next=h; h=t;

14、已知单链表中结点 p不是链尾结点，若在 p之后插入结点s，则应执行 以下（D）操作。

1. s->link = p; p->link=s;
2. p->link=s; s->link=p;
3. s->link=p->link; p=s；
4. s->link=p->link; p->link=s;

15、在具有N个结点的单链表中，实现下列哪个操作，其算法的时间复杂度是O(N)？ ©

1. 在地址为p的结点之后插入一个结点
2. 删除开始结点
3. 遍历链表和求链表的第i个结点
4. 删除地址为p的结点的后继结点

16、带头结点的单链表h为空的判定条件是： (B)

1. h == NULL;
2. h->next == NULL;
3. h->next == h;
4. h != NULL;

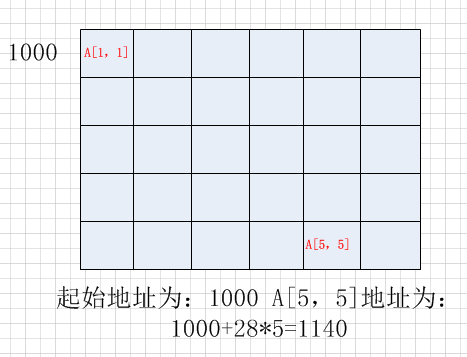
17、数组 A[1…5,1…6]每个元素占 5 个单元，将其按行优先次序存储在起始地址为 1000 的连续的
内存单元中，则元素 A[5,5]的地址为：©

1. 1120
2. 1125
3. 1140
4. 1145

解析：

18、数据结构反映了数据元素之间的结构关系。单链表是一种（D）。

1. 顺序存储线性表
2. 非顺序存储非线性表
3. 顺序存储非线性表
4. 非顺序存储线性表

19、对于一非空的循环单链表，h 和 p 分别指向链表的头、尾结点，则有：(A)

1. p->next == h
2. p->next == NULL
3. p == NULL
4. p == h

20、单链表又称为线性链表，在单链表上实施插入和删除操作（）。 (B)

1. 不需移动结点，不需改变结点指针
2. 不需移动结点，只需改变结点指针
3. 只需移动结点，不需改变结点指针
4. 既需移动结点，又需改变结点指针

三、程序填空

头插法建立单链表

#include 
#include 

typedef int ElemType;
typedef struct LNode
{
	ElemType data;
	struct LNode *next;
}LNode,*LinkList;

LinkList Create();
void print( LinkList L);

int main()
{
	  LinkList L = Create();
	  print(L);
	  return 0;
}
LinkList Create()
{
	LinkList L,s;
	ElemType e;
	L = (LinkList)malloc(sizeof(LNode));
	L->next = NULL;//填空
	scanf("%d",&e);
	while(e!=-1)
	{
		s = (LinkList)malloc(sizeof(LNode));
		s->data=e;
		s->next = L->next;//填空
		L->next = s;//填空
		scanf("%d",&e);
	}
    return L;//填空
}
void print(LinkList L)
{ 
	LinkList p;
        p=L->next;
	while (p)
	{
	     printf("%d ", p->data);
 	     p =p->next;
	}
}

输入格式：

输入数据为若干正整数，最后以-1表示结尾（-1不算在序列内，不要处理）。所有数据之间用空格分隔。

输入样例：

1 2 3 4 5 6 7 8 9  -1

输出样例：

9 8 7 6 5 4 3 2 1 

解析：

四、函数题

1、本题要求实现一个函数，将给定单向链表逆置，即表头置为表尾，表尾置为表头。链表结点定义如下：

struct ListNode {
    int data;
    struct ListNode *next;
};

函数接口定义：

struct ListNode *reverse( struct ListNode *head );

其中head是用户传入的链表的头指针；函数reverse将链表head逆置，并返回结果链表的头指针。

裁判测试程序样例：

#include 
#include 
struct ListNode {
    int data;
    struct ListNode *next;
};
struct ListNode *createlist(); /*裁判实现，细节不表*/
struct ListNode *reverse( struct ListNode *head );
void printlist( struct ListNode *head )
{
     struct ListNode *p = head;
     while (p) {
           printf("%d ", p->data);
           p = p->next;
     }
     printf("\n");
}

int main()
{
    struct ListNode  *head;
    head = createlist();
    head = reverse(head);
    printlist(head);
	
    return 0;
}

/* 你的代码将被嵌在这里 */

输入样例：

1 2 3 4 5 6 -1

输出样例：

6 5 4 3 2 1 

实现代码：

struct ListNode *reverse( struct ListNode *head ){
    struct ListNode * q=NULL,*r=NULL;
    while(head){
        q=head;
        head=head->next;
        q->next=r;
        r=q;
    }
    return q;
}

裁判代码实现：

struct ListNode *createlist(){
	int data;
	struct ListNode * head=NULL,*p,*q;
	scanf("%d",&data);
	while(data!=-1){
		p=(struct ListNode *)malloc(sizeof(struct ListNode));
		p->data=data;
		if(head==NULL)
			head=p;
		else
			q->next=p;
		q=p;
		scanf("%d",&data);
	}
	q->next=NULL;
	return head;
}

2、线性表元素的区间删除
给定一个顺序存储的线性表，请设计一个函数删除所有值大于 min 而且小于 max 的元素。删除后表中剩余元素保持顺序存储，并且相对位置不能改变。
函数接口定义：

List Delete( List L, ElementTypeminD, ElementTypemaxD );

其中 List 结构定义如下：

typedefint Position;
typedef struct LNode *List;
struct LNode {
	ElementType Data[MAXSIZE];
 	Position Last; /* 保存线性表中最后一个元素的位置 */
};

L 是用户传入的一个线性表，其中 ElementType 元素可以通过>、==、<进行比较；minD 和maxD 分别为待删除元素的值域的下、上界。函数 Delete 应将 Data[]中所有值大于 minD 而且小于 maxD 的元素删除，同时保证表中剩余元素保持顺序存储，并且相对位置不变，最后返回删除后的表。
裁判测试程序样例：

#include 
#define MAXSIZE 20
typedef int ElementType;
typedef int Position;
typedef struct LNode *List;
struct LNode {
	ElementType Data[MAXSIZE];
	Position Last; /* 保存线性表中最后一个元素的位置 */
};
List ReadInput(); /* 裁判实现，细节不表。元素从下标 0 开始存储 */
void PrintList( List L ); /* 裁判实现，细节不表 */
List Delete( List L, ElementTypeminD, ElementTypemaxD );
int main()
{
 	List L;
	ElementTypeminD, maxD;
	inti;
 	L = ReadInput();
	scanf("%d %d", &minD, &maxD);
 	L = Delete( L, minD, maxD );
	PrintList( L );
	return 0;
}
/* 你的代码将被嵌在这里 */

输入样例：
10
4 -8 2 12 1 5 9 3 3 10
0 4
输出样例：
4 -8 12 5 9 10
实现代码：

List Delete( List L, ElementType minD, ElementType maxD ){
	int data[MAXSIZE],k=0;
	for(int i=0;i<=L->Last;i++){
		if(L->Data[i]<=minD||L->Data[i]>=maxD)
			data[k++]=L->Data[i]; 
	} 
	L->Last=k-1;
	for(int i=0;i<k;i++)
		L->Data[i]=data[i];
	return L;
} 

裁判实现：

void PrintList( List L ){
	for(int i=0;i<=L->Last;i++)
		printf("%d ",L->Data[i]);
}
List ReadInput(){
	int n;
	List L;
	scanf("%d",&n);
	for(int i=0;i<n;i++)
		scanf("%d",&L->Data[i]);
	L->Last=n-1;		
	return L;
}

如有错误，或者某道题解析不详细，请指出；
下一节：算法与数据结构复习 第三章 栈与队列（详解)