leetcode核心思想:双指针,数字小的那个指针移动classSolution{public:intmaxArea(vector&height){intleft=0;intright=height.size()-1;intmaxArea=0;while(left
leetcode刷题day13|二叉树Part01(递归遍历、迭代遍历、统一迭代、层序遍历)
小冉在学习
leetcode算法职场和发展
递归遍历思路:使用递归的方式比较简单。1、递归函数的传参:因为最后输出一个数组,所以需要传入根节点和一个容器,本来想写数组,但发现长度不能确定,所以选择list。2、终止条件:当访问的节点为空时,return3、递归函数的逻辑:先访问一个节点,递归访问其他节点144.二叉树的前序遍历代码如下:classSolution{publicListpreorderTraversal(TreeNoderoo
leetcode021-合并两个有序链表
陆阳226
问题描述将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。示例:输入:1->2->4,1->3->4输出:1->1->2->3->4->4解答递归法:每一层减去一个较小的节点,直到某个链表为null递归结束。publicstaticListNodesolution(ListNodel1,ListNodel2){if(l1==null){returnl2;}
每日一题《leetcode--LCR 022.环形链表||》
Peace & Love487
题目分享leetcode链表算法笔记数据结构
https://leetcode.cn/problems/c32eOV/我们使用两个指针,fast与slow。它们起始都位于链表的头部。随后slow指针每次向后移动一个位置,而fast指针向后移动两个位置。如果链表中存在环,则fast指针最终将再次与slow指针在环中相遇。structListNode*detectCycle(structListNode*head){structListNode*
LCR 078. 合并 K 个升序链表
装B且挨揍の
LeetCode链表算法数据结构经验分享笔记java
https://leetcode.cn/problems/vvXgSW/description/https://leetcode.cn/problems/vvXgSW/description/解题思路方法一:每个链表维护一个索引,每次找到值最小的节点,索引加一。可以采用优先队列实现。/***Definitionforsingly-linkedlist.*publicclassListNode{*i
LeetCode:2390. 从字符串移除*号 使用栈,时间复杂度O(N)
忍界英雄
每日一题leetcodelinux算法
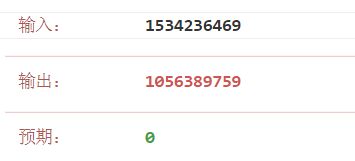
2390.从字符串移除*号today2390.从字符中移除*号题目表述给你一个包含若干星号*的字符串s。在一步操作中,你可以:选中s中的一个星号。移除星号左侧最近的那个非星号字符,并移除该星号自身。返回移除所有星号之后的字符串。注意:生成的输入保证总是可以执行题面中描述的操作。可以证明结果字符串是唯一的。示例1:输入:s=“leet**cod*e”输出:“lecoe”解释:从左到右执行移除操作:距
⭐算法入门⭐《归并排序》简单01 —— LeetCode 21. 合并两个有序链表
英雄哪里出来
《LeetCode算法全集》算法数据结构链表c++归并排序
饭不食,水不饮,题必须刷C语言免费动漫教程,和我一起打卡!《光天化日学C语言》LeetCode太难?先看简单题!《C语言入门100例》数据结构难?不存在的!《数据结构入门》LeetCode太简单?算法学起来!《夜深人静写算法》文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识一、题目1、题目描述 将两个不降序链表合并为一个新的不降
【LeetCode 算法笔记】84. 柱状图中最大的矩形
Sardar_
算法leetcode笔记
目录问题描述暴力求解:栈问题描述给定n个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为1。求在该柱状图中,能够勾勒出来的矩形的最大面积。示例1:输入:heights=[2,1,5,6,2,3]输出:10解释:最大的矩形为图中红色区域,面积为10示例2:输入:heights=[2,4]输出:4提示:1int:area=0n=len(heights)foriinrange(n):
【LeetCode 算法笔记】739. 每日温度
Sardar_
算法leetcode笔记
目录问题描述暴力解法栈问题描述给定一个整数数组temperatures,表示每天的温度,返回一个数组answer,其中answer[i]是指对于第i天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用0来代替。示例1:输入:temperatures=[73,74,75,71,69,72,76,73]输出:[1,1,4,2,1,1,0,0]示例2:输入:temperatures=
面试题24. 反转链表
阿星啊阿星
反转链表题目描述定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点示例:输入:1->2->3->4->5->NULL输出:5->4->3->2->1->NULL提示:0<=节点个数<=5000转载来源:力扣(LeetCode)题目分析1→2→3→null初始化时h为1,now为2,h的next设置成null,有:null←1(h) 2(now)→3现在将保存一下now的next
【数据结构和算法实践-树-LeetCode113-路径总和Ⅱ】
NeVeRMoRE_2024
数据结构与算法实践数据结构算法leetcodeb树
数据结构和算法实践-树-LeetCode113-路径总和Ⅱ题目MyThought代码示例JAVA-8题目给你二叉树的根节点root和一个整数目标和targetSum,找出所有从根节点到叶子节点路径总和等于给定目标和的路径。叶子节点是指没有子节点的节点输入:root=[5,4,8,11,null,13,4,7,2,null,null,5,1],targetSum=22输出:[[5,4,11,2],[
单词搜索 II
xialu
来源:力扣(LeetCode)链接:https://leetcode-cn.com/problems/word-search-ii题目描述:给定一个mxn二维字符网格board和一个单词(字符串)列表words,找出所有同时在二维网格和字典中出现的单词。单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重
Spring4.1新特性——Spring MVC增强
jinnianshilongnian
spring 4.1
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
mysql 性能查询优化
annan211
javasql优化mysql应用服务器
1 时间到底花在哪了?
mysql在执行查询的时候需要执行一系列的子任务,这些子任务包含了整个查询周期最重要的阶段,这其中包含了大量为了
检索数据列到存储引擎的调用以及调用后的数据处理,包括排序、分组等。在完成这些任务的时候,查询需要在不同的地方
花费时间,包括网络、cpu计算、生成统计信息和执行计划、锁等待等。尤其是向底层存储引擎检索数据的调用操作。这些调用需要在内存操
windows系统配置
cherishLC
windows
删除Hiberfil.sys :使用命令powercfg -h off 关闭休眠功能即可:
http://jingyan.baidu.com/article/f3ad7d0fc0992e09c2345b51.html
类似的还有pagefile.sys
msconfig 配置启动项
shutdown 定时关机
ipconfig 查看网络配置
ipconfig /flushdns
人体的排毒时间
Array_06
工作
========================
|| 人体的排毒时间是什么时候?||
========================
转载于:
http://zhidao.baidu.com/link?url=ibaGlicVslAQhVdWWVevU4TMjhiKaNBWCpZ1NS6igCQ78EkNJZFsEjCjl3T5EdXU9SaPg04bh8MbY1bR
ZooKeeper
cugfy
zookeeper
Zookeeper是一个高性能,分布式的,开源分布式应用协调服务。它提供了简单原始的功能,分布式应用可以基于它实现更高级的服务,比如同步, 配置管理,集群管理,名空间。它被设计为易于编程,使用文件系统目录树作为数据模型。服务端跑在java上,提供java和C的客户端API。 Zookeeper是Google的Chubby一个开源的实现,是高有效和可靠的协同工作系统,Zookeeper能够用来lea
网络爬虫的乱码处理
随意而生
爬虫网络
下边简单总结下关于网络爬虫的乱码处理。注意,这里不仅是中文乱码,还包括一些如日文、韩文 、俄文、藏文之类的乱码处理,因为他们的解决方式 是一致的,故在此统一说明。 网络爬虫,有两种选择,一是选择nutch、hetriex,二是自写爬虫,两者在处理乱码时,原理是一致的,但前者处理乱码时,要看懂源码后进行修改才可以,所以要废劲一些;而后者更自由方便,可以在编码处理
Xcode常用快捷键
张亚雄
xcode
一、总结的常用命令:
隐藏xcode command+h
退出xcode command+q
关闭窗口 command+w
关闭所有窗口 command+option+w
关闭当前
mongoDB索引操作
adminjun
mongodb索引
一、索引基础: MongoDB的索引几乎与传统的关系型数据库一模一样,这其中也包括一些基本的优化技巧。下面是创建索引的命令: > db.test.ensureIndex({"username":1}) 可以通过下面的名称查看索引是否已经成功建立: &nbs
成都软件园实习那些话
aijuans
成都 软件园 实习
无聊之中,翻了一下日志,发现上一篇经历是很久以前的事了,悔过~~
断断续续离开了学校快一年了,习惯了那里一天天的幼稚、成长的环境,到这里有点与世隔绝的感觉。不过还好,那是刚到这里时的想法,现在感觉在这挺好,不管怎么样,最要感谢的还是老师能给这么好的一次催化成长的机会,在这里确实看到了好多好多能想到或想不到的东西。
都说在外面和学校相比最明显的差距就是与人相处比较困难,因为在外面每个人都
Linux下FTP服务器安装及配置
ayaoxinchao
linuxFTP服务器vsftp
检测是否安装了FTP
[root@localhost ~]# rpm -q vsftpd
如果未安装:package vsftpd is not installed 安装了则显示:vsftpd-2.0.5-28.el5累死的版本信息
安装FTP
运行yum install vsftpd命令,如[root@localhost ~]# yum install vsf
使用mongo-java-driver获取文档id和查找文档
BigBird2012
driver
注:本文所有代码都使用的mongo-java-driver实现。
在MongoDB中,一个集合(collection)在概念上就类似我们SQL数据库中的表(Table),这个集合包含了一系列文档(document)。一个DBObject对象表示我们想添加到集合(collection)中的一个文档(document),MongoDB会自动为我们创建的每个文档添加一个id,这个id在
JSONObject以及json串
bijian1013
jsonJSONObject
一.JAR包简介
要使程序可以运行必须引入JSON-lib包,JSON-lib包同时依赖于以下的JAR包:
1.commons-lang-2.0.jar
2.commons-beanutils-1.7.0.jar
3.commons-collections-3.1.jar
&n
[Zookeeper学习笔记之三]Zookeeper实例创建和会话建立的异步特性
bit1129
zookeeper
为了说明问题,看个简单的代码,
import org.apache.zookeeper.*;
import java.io.IOException;
import java.util.concurrent.CountDownLatch;
import java.util.concurrent.ThreadLocal
【Scala十二】Scala核心六:Trait
bit1129
scala
Traits are a fundamental unit of code reuse in Scala. A trait encapsulates method and field definitions, which can then be reused by mixing them into classes. Unlike class inheritance, in which each c
weblogic version 10.3破解
ronin47
weblogic
版本:WebLogic Server 10.3
说明:%DOMAIN_HOME%:指WebLogic Server 域(Domain)目录
例如我的做测试的域的根目录 DOMAIN_HOME=D:/Weblogic/Middleware/user_projects/domains/base_domain
1.为了保证操作安全,备份%DOMAIN_HOME%/security/Defa
求第n个斐波那契数
BrokenDreams
今天看到群友发的一个问题:写一个小程序打印第n个斐波那契数。
自己试了下,搞了好久。。。基础要加强了。
&nbs
读《研磨设计模式》-代码笔记-访问者模式-Visitor
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.List;
interface IVisitor {
//第二次分派,Visitor调用Element
void visitConcret
MatConvNet的excise 3改为网络配置文件形式
cherishLC
matlab
MatConvNet为vlFeat作者写的matlab下的卷积神经网络工具包,可以使用GPU。
主页:
http://www.vlfeat.org/matconvnet/
教程:
http://www.robots.ox.ac.uk/~vgg/practicals/cnn/index.html
注意:需要下载新版的MatConvNet替换掉教程中工具包中的matconvnet:
http
ZK Timeout再讨论
chenchao051
zookeepertimeouthbase
http://crazyjvm.iteye.com/blog/1693757 文中提到相关超时问题,但是又出现了一个问题,我把min和max都设置成了180000,但是仍然出现了以下的异常信息:
Client session timed out, have not heard from server in 154339ms for sessionid 0x13a3f7732340003
CASE WHEN 用法介绍
daizj
sqlgroup bycase when
CASE WHEN 用法介绍
1. CASE WHEN 表达式有两种形式
--简单Case函数
CASE sex
WHEN '1' THEN '男'
WHEN '2' THEN '女'
ELSE '其他' END
--Case搜索函数
CASE
WHEN sex = '1' THEN
PHP技巧汇总:提高PHP性能的53个技巧
dcj3sjt126com
PHP
PHP技巧汇总:提高PHP性能的53个技巧 用单引号代替双引号来包含字符串,这样做会更快一些。因为PHP会在双引号包围的字符串中搜寻变量, 单引号则不会,注意:只有echo能这么做,它是一种可以把多个字符串当作参数的函数译注: PHP手册中说echo是语言结构,不是真正的函数,故把函数加上了双引号)。 1、如果能将类的方法定义成static,就尽量定义成static,它的速度会提升将近4倍
Yii框架中CGridView的使用方法以及详细示例
dcj3sjt126com
yii
CGridView显示一个数据项的列表中的一个表。
表中的每一行代表一个数据项的数据,和一个列通常代表一个属性的物品(一些列可能对应于复杂的表达式的属性或静态文本)。 CGridView既支持排序和分页的数据项。排序和分页可以在AJAX模式或正常的页面请求。使用CGridView的一个好处是,当用户浏览器禁用JavaScript,排序和分页自动退化普通页面请求和仍然正常运行。
实例代码如下:
Maven项目打包成可执行Jar文件
dyy_gusi
assembly
Maven项目打包成可执行Jar文件
在使用Maven完成项目以后,如果是需要打包成可执行的Jar文件,我们通过eclipse的导出很麻烦,还得指定入口文件的位置,还得说明依赖的jar包,既然都使用Maven了,很重要的一个目的就是让这些繁琐的操作简单。我们可以通过插件完成这项工作,使用assembly插件。具体使用方式如下:
1、在项目中加入插件的依赖:
<plugin>
php常见错误
geeksun
PHP
1. kevent() reported that connect() failed (61: Connection refused) while connecting to upstream, client: 127.0.0.1, server: localhost, request: "GET / HTTP/1.1", upstream: "fastc
修改linux的用户名
hongtoushizi
linuxchange password
Change Linux Username
更改Linux用户名,需要修改4个系统的文件:
/etc/passwd
/etc/shadow
/etc/group
/etc/gshadow
古老/传统的方法是使用vi去直接修改,但是这有安全隐患(具体可自己搜一下),所以后来改成使用这些命令去代替:
vipw
vipw -s
vigr
vigr -s
具体的操作顺
第五章 常用Lua开发库1-redis、mysql、http客户端
jinnianshilongnian
nginxlua
对于开发来说需要有好的生态开发库来辅助我们快速开发,而Lua中也有大多数我们需要的第三方开发库如Redis、Memcached、Mysql、Http客户端、JSON、模板引擎等。
一些常见的Lua库可以在github上搜索,https://github.com/search?utf8=%E2%9C%93&q=lua+resty。
Redis客户端
lua-resty-r
zkClient 监控机制实现
liyonghui160com
zkClient 监控机制实现
直接使用zk的api实现业务功能比较繁琐。因为要处理session loss,session expire等异常,在发生这些异常后进行重连。又因为ZK的watcher是一次性的,如果要基于wather实现发布/订阅模式,还要自己包装一下,将一次性订阅包装成持久订阅。另外如果要使用抽象级别更高的功能,比如分布式锁,leader选举
在Mysql 众多表中查找一个表名或者字段名的 SQL 语句
pda158
mysql
在Mysql 众多表中查找一个表名或者字段名的 SQL 语句:
方法一:SELECT table_name, column_name from information_schema.columns WHERE column_name LIKE 'Name';
方法二:SELECT column_name from information_schema.colum
程序员对英语的依赖
Smile.zeng
英语程序猿
1、程序员最基本的技能,至少要能写得出代码,当我们还在为建立类的时候思考用什么单词发牢骚的时候,英语与别人的差距就直接表现出来咯。
2、程序员最起码能认识开发工具里的英语单词,不然怎么知道使用这些开发工具。
3、进阶一点,就是能读懂别人的代码,有利于我们学习人家的思路和技术。
4、写的程序至少能有一定的可读性,至少要人别人能懂吧...
以上一些问题,充分说明了英语对程序猿的重要性。骚年
Oracle学习笔记(8) 使用PLSQL编写触发器
vipbooks
oraclesql编程活动Access
时间过得真快啊,转眼就到了Oracle学习笔记的最后个章节了,通过前面七章的学习大家应该对Oracle编程有了一定了了解了吧,这东东如果一段时间不用很快就会忘记了,所以我会把自己学习过的东西做好详细的笔记,用到的时候可以随时查找,马上上手!希望这些笔记能对大家有些帮助!
这是第八章的学习笔记,学习完第七章的子程序和包之后