szu 寒训第二天 树状数组 二维树状数组详解，以及树状数组扩展应用【求逆序对，以及动态第k小数】

树状数组（Binary Index Tree）

树状数组可以解决可以转化为前缀和问题的问题

---------这是一类用以解决动态前缀和的问题
（有点像线段树简版）

**1.对于
a1 + a2 + a3 + … + an

1）询问 aj + … + am (1 <= j <= m <= n );
2) 修改 ai ( 1<= i <= n);
（yxc大佬说任何问题都要树立暴力思想）
那么暴力的复杂度是多少呢？
很明显是 O（n ^ 2）的qwq;**

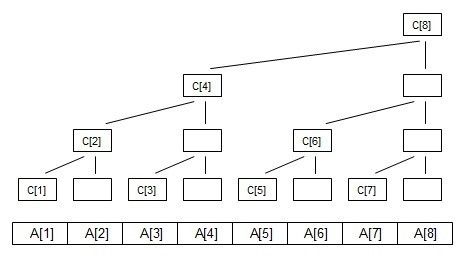
下面来一张百度百科的图片了解一下树状数组的基本构造

通过这张图我们可以发现在某一个位置的值它存储的不仅仅是它自己的值。
比如说12这个点它存储的是9到12的前缀和，而7只存储自己的值，这是什么规律呢？

这里有一个有趣的性质:

设节点编号为x，那么这个节点管辖的区间为2^k(其中k为x二进制末尾0的个数)个元素。因为这个区间最后一个元素必然为Ax，
所以很明显:Cn = A(n – 2^k + 1) + … + An

是不是很难懂？ 那我们来举个栗子：

通过图片可知
d[6] = a5 + a6; 而 6的二进制表示是什么呢110 因为末尾0的个数是1所以6这个位置要存储2 ^ 1个数位
d[8] = a1 + … + a8 ；
8的二进制表示是1000 所以是2^3次方个数

那么这是查询的复杂度是多少呢(log级别)

为什么复杂度被log了呢?可以看到，C8可以看作A1~A8的左半边和 + 右半边和，而其中左半边和是确定的C4，右半边其实也是同样的规则把A5 ~ A8一分为二……继续下去都是一分为二直到不能分树状数组巧妙地利用了二分，树状数组并不神秘，关键是巧妙!
实际上它长这样

下面是查询值啦

比如说我们要查询13这个位置的前缀和
1.(13)10 = (1101)2 进制转换
注意因为树状数组是根据二进制存值的那么查询的时候我们要进行二进制的拆分
2.1101 = 13
1100 = 12
1000 = 8
我们要询问13位置的前缀和只需要把这几个数加起来就好了 下面再看一下图 我们发现刚好是13的前缀和

3.我们再来看一下这3个数的管辖区间
1101 = 13 2 ^ 0
1100 = 12 2 ^ 2
1000 = 8 2 ^ 3
加起来刚好和13相等

所以在查询操作实际上是每一次将二进制位的值最后一个0给抹掉

这里我们引入一个定理 1~2的n次方可以拼出 1 ~ 2^n-1次方中任意一个数（之后多重背包问题的二进制优化版本会提到）

下面就是对树状数组进行区间修改

我们再把这张图贴一下

下面来看这个末尾的1的位置怎么找

祭：lowbit 算法

lowbit(int x)
{
return x & (-x)
}
为啥是这么写呢
12 = 1100
-12 在计算机中存储的方式是（~12 + 1）
也就是补码形式 = 0100
两个相&结果就是0100这样就找到最后的1了

/*
树状数组动态询问前缀和
 修改加 lowbit
 查询减 lowbit
 关建就是树状数组下标不能为 0  
*/
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define root rt;
#define mid ((l + r) >> 1)
#define Lson rt << 1, l , mid
#define Rson rt << 1|1, mid + 1, r
#define INF 0x3f3f3f3f
#define mst(a,b) memset((a),(b),sizeof(a)) 
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PII;
const int M = 3e5 + 10;
PII start[M << 2];
int d[M << 2];
int level[M];
inline int lowbit(int x)
{
   return x & (-x);	
} 

inline int query(int x)
{
	int res = 0;
	while(x)
	{
		res += d[x];
		x -= lowbit(x);
	}
	return res;
}

这就是求前缀和的操作，还有提醒一点就是树状数组的下标是从1开始的（我之前从0开始一直tle qwq）下面来看一下区间修改

假如说我们要对3这个位置进行修改那么我们还要修改覆盖3的区间比如说4，8，16这上三个区间的值都要修改上次我们在查询的时候是把末尾的一依次抹掉现在我们反过过来依次加上去
比如说 (3)10 = (11)2;
11 的 最后一个1在个位就 + 1
||（变成下面）
100 = 4(这时候1在第三位)+100
||
1000 = 8（依此类推）
…

下面就是区间修改的代码

inline void add(int x, int v,int n)
{
	while(x <= n)
	{
		d[x] += v;
		x += lowbit(x);
	}
}

区间和操作[5 ~ 8]
sum(8) - sum(4) //是不是很简单qwq

下面来看树状数组的区间修改和单点查询问题

在这个问题中我们需要完成的任务是：
将一个区间内的数字增加同样一个值
求某一个位置的值。
在这里我们可以利用差分的思想，假设初始数组为A，我们首先构造一个关于A的差分数组C,其中$C[1]=A[1],C[i]=A[i]-[Ai-1]$。
那么我们想将区间[L,R]内的数字增加同样一个值，那么我们只需要修改差分数组中两个位置的元素C[L]=C[L]+delta,C[R+1]=C[R+1]−delta
如果我们想要求某一个位置的值A[idx]，那么A[idx]=sumRange(C[1,idx])

那么这颗树就是差分树

下面上代码

inline int lowbit(int x)
{
   return x & (-x);	
} 

inline int query(int x)
{
	int res = 0;
	while(x)
	{
		res += d[x];
		x -= lowbit(x);
	}
	return res;
}
inline void add(int x, int v,int n)
{
	while(x <= n)
	{
		d[x] += v;
		x += lowbit(x);
	}
}
void init(int a[])
{
	for(int i = 1; i <= n; ++ i)
	{
		c[i] = a[i] - a[i - 1];
		add(i,c[i],n);//在区间i~n的区间内满足的数组位置加c[i]; 
	}
} 

void undate(int l, int r, int d)
{
	add(l,d,n);
	add(r,-d,n);
}

因为前缀和跟差分是一对互逆运算 所以单点查询也就是sum(n) = 该点的值;

下面再来看看区间修改和区间查询的树状数组

b是差分数组

通过观察可知我们我们需要两树状数组

一个储存（n+)*(c[1~n])

另一个存储 i* c[i] 的和

板子来咯

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define mid ((l + r) >> 1) 
#define Lson rt << 1, l , mid
#define Rson rt << 1|1, mid + 1, r
#define ms(a,al) memset(a,al,sizeof(a))
#define sfx(x) scanf("%lf",&x)
#define sfxy(x,y) scanf("%lf%lf",&x,&y)
#define sdx(x) scanf("%d",&x)
#define sdxy(x,y) scanf("%d%d",&x,&y)
#define pfx(x) printf("%.0f\n",x)
#define pfxy(x,y) printf("%.6f %.6f\n",x,y)
#define pdx(x) printf("%d\n",x)
#define pdxy(x,y) printf("%d %d\n",x,y)
#define _for(i,a,b) for( int i = (a); i < (b); ++i)
#define _rep(i,a,b) for( int i = (a); i <= (b); ++i)
#define for_(i,a,b) for( int i = (a); i >= (b); -- i)
#define rep_(i,a,b) for( int i = (a); i > (b); -- i)
#define lowbit(x) ((-x) & x)
#define IOS std::ios::sync_with_stdio(0); cin.tie(0); cout.tie(0)
#define INF 0x3f3f3f3f
#define hash Hash
#define next Next
#define f first
#define s second
using namespace std;
const int N = 2e5 + 10, eps = 1e-10;
typedef long long LL;
typedef unsigned long long ULL;

int n, m;
LL tr1[N];//b[i]的前缀和，b[i]是差分数组
LL tr2[N];//维护b[i] * i 的前嘴和
LL a[N];

void add(LL tr[], int x, LL c)
{
    while(x <= n)
    {
        tr[x] += c;    
        x += lowbit(x);
    }
}

LL sum(LL tr[], int x)
{
    LL res = 0;
    while(x)
    {
        res += tr[x];
        x -=lowbit(x);
    }
    return res;
}

LL prefix_sum(int x)//求a[i]的前缀和
{
    return sum(tr1,x) * (x + 1) - sum(tr2, x);
}

int main()
{
    IOS;
    cin >> n >> m;
    _for(i,1,n+1) cin >> a[i];
    _for(i,1,n+1)
    {
        int b = a[i] - a[i - 1];
        add(tr1, i, b);
        add(tr2, i, (LL)b * i);
    }
    while(m -- )
    {
        char op[2];
        int l, r, d;
        cin >> op >> l >> r;
        if(*op == 'Q')
            cout << prefix_sum(r) - prefix_sum(l - 1) << endl;
        else 
        {
            cin >> d;
            //a[l]的位置加上d;
            add(tr1,l,d); add(tr2,l,d * l);
            //a[r + 1] -= d;
            add(tr1,r + 1, -d); add(tr2,r + 1,(r + 1) * (-d));
        }
    }
	return 0;
}

下面最后一个专题就是二维树状数组

这个就比较简单惹qwq
(板子好背原理不太懂)
我们需要两种操作
1.修改（x,y）;
2求（x,y）

inline int lowbit(int x)
{
	return x & (-x);
}

void add(int x,int y,int v)
{
	for(int i = x; i <= n; i += lowbit(i))
	  for(int j = y; j <= n;j += lowbit(j));
	   a[i][j] += v;
}

void query(int x, int y)
{
	int res = 0;
	for(int i = x; i ; i -= lowbit(i))
	  for(int j = y; j; j -= lowbit(j))
	   res += a[i][j]; 
}

//-----------------------------------------------------
szu寒训题解个人版
1)
HDU6318 Swaps and Inversions
这个题就是说给你一个序列这个序列里你每存在一个逆序数对你就会被罚款x元，你也可以提前修改这个序列每修过一次是y元，你只能交换相邻的位置的数

我们发现假设这个序列有n对逆序对，那么我们需要执行n次置换将其还原
答案就是 min(x,y) * 逆序对

我是用归并水过去的qwq
现在来讲一下树状数组的求法
感觉比较难像qwq

逆序对的定义 : i < j && a[i] > a[j] ；
用树状数组求要用到离散化我们在day1线段树的博客有讲这里就不重复讲了。
因为逆序对是明显的对于数值具体不考虑
只考虑相对关系
假设有一序列（1，5，2，9，100）
//按大到小离散化
离散化后d[] =（5，3，4，2，1）
但不是求d中的逆序对了，而是求d中的正序对，来看一下怎么求的：
1.首先把5放进去tree中 比 5小的没有 res +=0；
2.把3放进去，此时有5，3比3小的也没有res += 0;
3.把 4 放进去 比 4小的有3 res += 1;
…
res = 1; 再计算原数组也是对的；

这时候树状数组的节点表示的是tree[x] 【1~x】有几个数已经存在；

#include 
#include 
#include 

using namespace  std;
typedef long long LL;
const int N = 1e6 + 10;
LL tree[N];//树状数组 
LL d[N];//离散数组 
LL a[N];//原数组 
LL n ,x, y;


LL lowbit(LL x)
{
    return x & (-x);	
} 

LL add(LL x)
{
	while(x <= n)//往后加就是告诉说有比你小的出现了 
	{
		tree[x] ++ ;
		x += lowbit(x);
	}
}

LL query(LL x)
{
   LL res = 0;
   while(x)
   {
     res += tree[x];
	 x -= lowbit(x);	
   }
   return res;	
} 

bool cmp(LL x, LL y)
{
	if(a[x] == a[y]) return x > y;
	else return a[x] > a[y];
}

int main()
{
	while(~scanf("%lld%lld%lld",&n,&x,&y))
	{
		memset(tree,0,sizeof(tree)); 
		for(int i = 1; i <= n; ++ i)
           scanf("%lld",&a[i]), d[i] = i;	
		   
		 sort(d + 1, d + 1 + n,cmp);
		//索引排序 
		LL ans = 0;
		
		for(int i = 1; i <= n; ++ i)
		{
			add(d[i]);//把这个数放进去 
			ans += query(d[i] - 1);//【1 ~ x-1】范围的数已经出现了多少 
		}
//		cout << ans << endl;
		printf("%lld\n",1LL*min(x,y) * ans);
	}
	return 0; 
}

数据范围要开long longqwq

总结：求先后顺序的题就可以用树状数组
处理在线处理法

poj2352

二维的逆序对qwq
给定n个点的n个坐标 求处每个点的左下方有多少个点并且按0个点1个点的顺将其分类再输出每个类有多少个点

这道题跟上面求逆序对数的思想差不多
我们可以一层一层的看在线处理按y坐标递增再到x坐标递增的顺序依次插入每次插入就进行一次询问就可以了

/*
树状数组动态询问前缀和
 修改加 lowbit
 查询减 lowbit
 关建就是树状数组下标不能为 0  
*/
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define root rt;
#define mid ((l + r) >> 1)
#define Lson rt << 1, l , mid
#define Rson rt << 1|1, mid + 1, r
#define INF 0x3f3f3f3f
#define mst(a,b) memset((a),(b),sizeof(a)) 
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PII;
const int M = 3e5 + 10;
PII start[M << 2];
int d[M << 2];
int level[M];
inline int lowbit(int x)
{
   return x & (-x);	
} 

inline int query(int x)
{
	int res = 0;
	while(x)
	{
		res += d[x];
		x -= lowbit(x);
	}
	return res;
}

inline void add(int x, int v,int n)
{
	while(x <= M)
	{
		d[x] += v;
		x += lowbit(x);
	}
}

int main()
{
	int mx = 0;
	int n;
	scanf("%d",&n);
	for(int i = 1; i <= n; ++ i) 
	{
		scanf("%d%d",&start[i].second,&start[i].first);
	     mx = max(start[i].second,mx);	
	}
		
	sort(start + 1,start + n + 1);
	for(int i = 1; i <= n; ++ i)
	{
        add(start[i].second + 1,1,mx);	//这里要加一；	
	    level[query(start[i].second + 1) - 1] ++ ;	
	}
	  
		for(int i = 0; i < n; ++ i)
		 printf("%d\n",level[i]);
	     cout.flush();	 
		 return 0;
}

树状数组求区间第k小数

AcWing 244. 谜一样的牛

有n头奶牛，已知它们的身高为 1~n 且各不相同，但不知道每头奶牛的具体身高。
现在这n头奶牛站成一列，已知第i头牛前面有Ai头牛比它低，求每头奶牛的身高。
解题思路：很明显我们可以从后面开始做因为最后一头牛的身高是可以确定的假设有ai头牛身高比它矮那么它身高就是ai + 1
那么树状数组的sum就是前面还有几个身高，可以用，那么我们可以先将树状数组每个位置加上1，然后删除的时候再加上-1就好了

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define mid ((l + r) >> 1) 
#define Lson rt << 1, l , mid
#define Rson rt << 1|1, mid + 1, r
#define ms(a,al) memset(a,al,sizeof(a))
#define sfx(x) scanf("%lf",&x)
#define sfxy(x,y) scanf("%lf%lf",&x,&y)
#define sdx(x) scanf("%d",&x)
#define sdxy(x,y) scanf("%d%d",&x,&y)
#define pfx(x) printf("%.0f\n",x)
#define pfxy(x,y) printf("%.6f %.6f\n",x,y)
#define pdx(x) printf("%d\n",x)
#define pdxy(x,y) printf("%d %d\n",x,y)
#define _for(i,a,b) for( int i = (a); i < (b); ++i)
#define _rep(i,a,b) for( int i = (a); i <= (b); ++i)
#define for_(i,a,b) for( int i = (a); i >= (b); -- i)
#define rep_(i,a,b) for( int i = (a); i > (b); -- i)
#define lowbit(x) ((-x) & x)
#define IOS std::ios::sync_with_stdio(0); cin.tie(0); cout.tie(0)
#define INF 0x3f3f3f3f
#define hash Hash
#define next Next
#define f first
#define s second
using namespace std;
const int N = 2e5 + 10, eps = 1e-10;
typedef long long LL;
typedef unsigned long long ULL;

int n, m;
int h[N], ans[N];
int tr[N];

void add(int x, int c)
{
    while(x <= n)
    {
        tr[x] += c;
        x += lowbit(x);
    }
}

LL sum(int x)
{
    LL res = 0;
    while(x)
    {
        res += tr[x];
        x -= lowbit(x);
    }
    return res;
}

int main()
{
    IOS;
    cin >> n;
    _for(i,2,n + 1) cin >> h[i];
    _for(i,1,n + 1) add(i,1);
    for_(i,n,1)
    {
        int k = h[i] + 1;
        int l = 1, r = n;
        while(l < r)
        {
            if(sum(mid) >= k) r = mid;
            else l = mid + 1;
        }
        ans[i] = l;
        add(r,-1);
    }
    _for(i,1,n+1)
      cout << ans[i] << endl;
      return 0;
}

打字不易，点个赞咯，有什么错误欢迎指正。