0x66.图论 - Tarjan算法与无向图连通性

声明：
本系列博客是《算法竞赛进阶指南》+《算法竞赛入门经典》+《挑战程序设计竞赛》的学习笔记，主要是因为我三本都买了 按照《算法竞赛进阶指南》的目录顺序学习，包含书中的少部分重要知识点、例题解题报告及我个人的学习心得和对该算法的补充拓展，仅用于学习交流和复习，无任何商业用途。博客中部分内容来源于书本和网络（我尽量减少书中引用），由我个人整理总结（习题和代码可全都是我自己敲哒）部分内容由我个人编写而成，如果想要有更好的学习体验或者希望学习到更全面的知识，请于京东搜索购买正版图书：《算法竞赛进阶指南》——作者李煜东，强烈安利，好书不火系列，谢谢配合。

---

下方链接为学习笔记目录链接（中转站）

学习笔记目录链接

---

ACM-ICPC在线模板

---

Tarjan算法与无向图连通性　　一句话总结
首先介绍了割点和割边（也称作桥），实际上性质差不多，通过使用时间戳和追溯值在整个图上判定割边和割点。割边：$low[v]>dfn[u]$割点：$low[v]\ge dfn[u]$以及割点需要特判根节点至少需要两个子结点满足条件，借助flag判定。由割边和割点引申出边双连通分量和点双连通分量，将割边或者割点“删除”即可得到相应的分量。这里的删除只是标记阻断即可，通过dfs求出连通块个数即为双连通分量的个数。实际运用时，由于有向图等的环等问题，可以将e-DCC或v-DCC缩点——找到标记并建立一个新图，在新图里将各各连通块缩成一个点，方便进行各种图中的应用。
因为是无向图，安排的明明白白的，所有的点都是联通的没有什么强连通分量的存在，所以要把点呀边呀割掉来制造强连通分量，而对于一张有向图，直接判定即可。

一、无向图的割点与桥

割点

对于图中一点，从图中删掉这个点和所有与这个点有关联的边之后,图就不是连通图,分裂成为了两个或两个以上不相连的子图，这样的点被称作该图的割点。

桥/割边

对于图中一边，删除这条边后,图就不是连通图,分裂成为两个不相连的子图. ，这样的边被称作该图的桥或者割边。

时间戳

按照图的深度优先遍历的过程，以每一个结点第一次被访问的顺序，依次赋值1~N的整数标记，该标记就被称为时间戳，标记了每一个结点的访问顺序，记作$dfn[x]$。

搜索树

具体定义详解见《算法竞赛进阶指南》P395

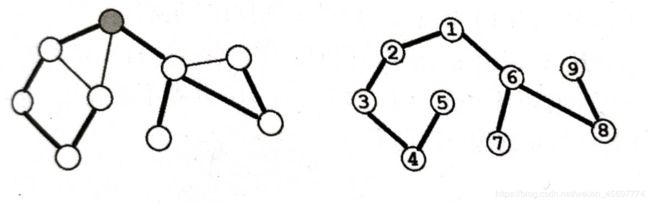
下图左侧是一张无向连通图，加粗的边是 “ 发生递归 ” 的边。
右侧是一棵搜索树，并标注了结点的时间戳。

追溯值

追溯值 $low[i]$

$dfn[i]$：表示第i个点的时间戳。

$low[i]$：表示点i及i的子树所能追溯到的最早的节点的时间戳。

$low[x]$定义为下列两种结点的时间戳的最小值。

1. 以x为根的子树上的结点。
2. 通过1条不在搜索树上的边，能够到达以x为根的子树上结点的结点。

首先令$low[x]=dfn[x]$，考虑从x出发的每条边$(x,y)$

若在搜索树上x是y的父结点(注意是无向图，双边)，则令$low[x]=min(low[x],low[y])$

若无向边$(x,y)$不是搜索树上的边，则令$low[x]=min(low[x],dfn[y])$

下图【 】中为该点的追溯值。

二、割边判定法则

割边$(u,v)$删去后变为两个连通块，v无法到达u前面的点，即
$$low[v]>dfn[u]$$

具体证明解析等见《算法竞赛进阶指南》P396

下面程序求出一张无向图中所有的桥，为了处理重边的情况，我们使用成对变换的技巧。

const int N = 1e5+7;//点数
const int M = 5e5+7;//边数
int head[M], ver[M], nex[M], tot = 1;//成对变换tot要初始化1，从2开始
int dfn[N], low[N];
int n, m, num;
bool bridge[M];

void add(int x,int y){
    ver[++tot] = y;
    nex[tot] = head[x];
    head[x] = tot;
}

void tarjan(int x,int in_edge){//当前结点 x 和前向星的编号 in_edge
    dfn[x] = low[x] = ++num;
    for(int i = head[x];i;i = nex[i]){
        int y = ver[i];
        if(!dfn[y]){
            tarjan(y,i);
            low[x] = min(low[x],low[y]);

            if(dfn[x] < low[y])
                bridge[i] = bridge[i ^ 1] = true;//利用成对变换的时候都是用的编号
        }
        else if(i != (in_edge ^ 1)){//若不是父结点
            low[x] = min(low[x],dfn[y]);//就更新
        }
    }
}

int main()
{
    cin>>n>>m;
    over(i,1,m){
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);add(y,x);
    }
    over(i,1,n)
        if(!dfn[i])//和有向图的操作一样
            tarjan(i,0);//注意是(i,0)
    for(int i = 2;i < tot;i += 2)//每次两个
        if(bridge[i])
            printf("%d %d\n",ver[i ^ 1],ver[i]);
    return 0;
}

三、割点判定法则

割点u删去后会有至少一个子树中的点无法到达u前面的点，即
存在至少一条树枝边$(u,v)$满足
$$low[v]\ge dfn[u]$$
对于根结点需要特别判断，只要有多于一条树枝边（两条及以上）则为割点。
由于割点判定法则为 $\le$ ,所以不需要考虑父结点及重边。
具体代码实现见下面给出的模板题

1.luogu P3388 【模板】割点（割顶）

割点模板题

#include
#include
#include
#include
#include
#include
#include
#include
#define ls (p<<1)
#define rs (p<<1|1)
#define over(i,s,t) for(register int i = s;i <= t;++i)
#define lver(i,t,s) for(register int i = t;i >= s;--i)
//#define int __int128
#define lowbit(p) p&(-p)
using namespace std;

typedef long long ll;
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 1e5+7;//点数
const int M = 5e5+7;//边数

int head[N], nex[M], ver[M], tot;
int n, m, num, root;
int stk[N], top;
int dfn[N], low[N];
bool cut[N];
int ans;

void add(int x,int y){
    ver[++tot] = y;
    nex[tot] = head[x];
    head[x] = tot;
}

void tarjan(int x){
    dfn[x] = low[x] = ++num;
    int flag = 0;
    for(int i = head[x];i;i = nex[i]){
        int y = ver[i];
        if(!dfn[y]){
            tarjan(y);
            low[x] = min(low[x],low[y]);
            if(low[y] >= dfn[x]){
                flag++;
                if(x != root || flag > 1)//不是根或者虽是根但是有两条边同时满足即为割点
                    cut[x] = true;
            }
        }
        else low[x] = min(low[x],dfn[y]);
    }
}

int main(){
    cin >> n >> m;
    over(i,1,m){
        int x,y;
        scanf("%d%d",&x,&y);
        if(x == y)continue;
        add(x,y);add(y,x);
    }
    over(i,1,n)
        if(!dfn[i])
            root = i,tarjan(i);
    over(i,1,n)if(cut[i])ans++;+
    printf("%d\n",ans);
    over(i,1,n)
    if(cut[i])
        printf("%d ",i);
    puts("");
    return 0;
}

2.luogu P3469 [POI2008]BLO-Blockade（割点判定 + 思维计算）

解题报告：luogu P3469 [POI2008]BLO-Blockade（割点判定 + 思维计算）

四、无向图的双连通分量

开始前的基础概念：

若一张无向连通图不存在割点，则称它为“点双连通图”，不存在桥则称为“边双连通图”。

无向图的极大点双连通子图就是“点双连通分量”：$v-DCC$，极大边双连通子图就是“边双连通分量”：$e-DCC$。

定理：

1. 一张无向连通图是点双连通图当且仅当 图的顶点数<=2 或者 图中任意两点都同时包含在至少一个简单环中。

2. 一张无向连通图是边双连通图当且仅当任意一条边都包含在至少一个简单环中。

1.边双连通分量($e-DCC$)的求法

e-DCC的求法很简单，通过一遍Tarjan算法找到所有的桥，把桥删除后，无向图会分裂成一个个连通块。

每一个连通块都是一个e-DCC。

具体实现就是先用Tarjan算法标记所有桥，然后对整张图dfs一遍(不访问桥边)，划分出所有连通块。

一般可以用一个数组c，表示每个节点所在的e-DCC的编号。

老规矩， 给出模板题以及AC代码

luogu T103489 【模板】边双连通分量

#include
#include
#include
#include
#include
#include
#include
#include
#define ls (p<<1)
#define rs (p<<1|1)
#define over(i,s,t) for(register int i = s;i <= t;++i)
#define lver(i,t,s) for(register int i = t;i >= s;--i)
//#define int __int128
#define lowbit(p) p&(-p)
using namespace std;

typedef long long ll;
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 5e5+7;
const int M = 5e6+7;

int ver[M],head[N],nex[M],tot = 1;
int c[N];// DCC 的编号
int dcc;//DCC 的数量,且是用来编号的
int dfn[N],low[N],cnt,num;
int n,m;
bool bridge[N];

inline void add(int x,int y){
    ver[++tot] = y;
    nex[tot] = head[x];
    head[x] = tot;
}
//in_edge是前向星的编号
void tarjan(int x,int in_edge){
    dfn[x] = low[x] = ++num;
    for(int i = head[x];i;i = nex[i]){
        int y = ver[i];
        if(!dfn[y]){
            tarjan(y,i);
            low[x] = min(low[x],low[y]);
            if(low[y] > dfn[x])//是割边
                bridge[i] = bridge[i ^ 1] = true;
        }
        else if(i != (in_edge ^ 1)){//不是父节点，没有回去
            low[x] = min(low[x],dfn[y]);
        }
    }
}

void dfs(int x){
    c[x] = dcc;
    for(int i = head[x];i;i = nex[i]){
        int y = ver[i];
        if(c[y] || bridge[i])continue;
        dfs(y);
    }
}

int main()
{
    cin>>n>>m;
    over(i,1,m){
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);add(y,x);
    }
    over(i,1,n)
        if(!dfn[i])//还是没有遍历到，说明是一个新的连通分量
            tarjan(i,0);
    over(i,1,n)
        if(!c[i])
            ++dcc,dfs(i);
    //over(i,1,n)
    //printf("%d belongs to DCC %d.\n",i,c[i]);
    cout<<dcc<<endl;
    return 0;
}

2.$e-DCC$的缩点

我们把每一个e-DCC都看成一个结点（只是看成结点），把所有桥边(x,y)看成连接编号为c[x]和c[y]的两个e-DCC间的边，这样我们就会得到一棵树或者森林(原图不连通)。并把e-DCC缩点生成的树(森林)储存在另一个邻接表中（新开一个链式前向星来存树）。

以下代码加在上面的那道边双连通分量模板的代码里即可

int hc[N],vc[M],nc[M],tc;
void add_c(int x,int y){
    vc[++tc] = y;
    nc[tc] = hc[x];
    hc[x] = tc;
}

//以下代码片段加在main函数里
{
    tc = 1;//因为要用到成对变换所以要初始化为1
    for(int i = 2;i <= tot;++i){//成对变换所以从2开始
        int x = ver[i ^ 1],y = ver[i];
        if(c[x] == c[y])continue;
        add_c(c[x],c[y]);
    }
    printf("缩点以后的森林，点数%d，边数%d(可能有重边)\n",dcc,tc / 2);
    for(int i = 2 ;i < tc;i += 2)//一对一对的
        printf("%d %d\n",vc[i ^ 1],vc[i]);
    return 0;
}

3.点双连通分量($v-DCC$)的求法

v-DCC是一个很容易混淆的概念。

由于v-DCC定义中的“极大”，一个割点可能属于多个v-DCC。

为了求出v-DCC，我们需要在Tarjan的过程中维护一个栈。

当一个点第一次被访问时，我们将它入栈。而当割点判定法则成立时，无论x是否为根，都要从栈顶不断弹出节点直到y节点被弹出，这些被弹出的节点包括x节点一起构成一个v-DCC。

#include
#include
#include
#include
#include
#include
#include
#include
#define ls (p<<1)
#define rs (p<<1|1)
#define over(i,s,t) for(register int i = s;i <= t;++i)
#define lver(i,t,s) for(register int i = t;i >= s;--i)
//#define int __int128
#define lowbit(p) p&(-p)
using namespace std;

typedef long long ll;
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 1e5+7;
const int M = 5e5+7;

int ver[M],head[N],nex[M],tot = 1;
int c[N];// DCC 的编号
vector<int> dcc[N];//DCC 的数量,且是用来编号的
int dfn[N],low[N],cnt,num;
int n,m,root;
int stk[N],top;
int cut[N];

inline void add(int x,int y){
    ver[++tot] = y;
    nex[tot] = head[x];
    head[x] = tot;
}

void tarjan(int x){
    dfn[x] = low[x] = ++num;
    stk[++top] = x;
    if(x == root && head[x] == 0){//孤立点
        dcc[++cnt].push_back(x);
        return ;
    }
    int flag = 0;
    for(int i = head[x];i;i = nex[i]){
        int y = ver[i];
        if(!dfn[y]){
            tarjan(y);
            low[x] = min(low[x],low[y]);
            if(low[y] >= dfn[x]){
                flag++;
                if(x != root || flag >1)cut[x] = true;
                cnt++;
                int z;
                do{
                    z = stk[top--];
                    dcc[cnt].push_back(z);
                }while(z != y);
                dcc[cnt].push_back(x);//最后把x放进去
            }
        }
        else low[x] = min(low[x],dfn[y]);
    }
}

int main()
{
    cin>>n>>m;
    over(i,1,m){
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);add(y,x);
    }
    over(i,1,n)
        if(!dfn[i])
            root = i,tarjan(i);//点双连通分量。不用判父节点
    over(i,1,cnt){
        printf("v-DCC #%d:",i);//第几个
        over(j,0,dcc[i].size())
        printf(" %d",dcc[i][j]);
        puts("");
    }
    return 0;
}

4.$v-DCC$的缩点

v-DCC的缩点由于一个割点可能在很多个v-DCC中而更加麻烦，但是我们也有办法缩。

假设图中有x个割点和y个v-DCC，我们就直接建(x+y)个点的新图。

每一个v-DCC和割点都作为新图的节点存在。建完后我们让每个割点和包含它的v-DCC连边。

#include
#include
#include
#include
#include
#include
#include
#include
#define ls (p<<1)
#define rs (p<<1|1)
#define over(i,s,t) for(register int i = s;i <= t;++i)
#define lver(i,t,s) for(register int i = t;i >= s;--i)
//#define int __int128
#define lowbit(p) p&(-p)
using namespace std;

typedef long long ll;
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 1e5+7;
const int M = 5e5+7;

int ver[M],head[N],nex[M],tot = 1;
int c[N];// DCC 的编号
vector<int> dcc[N];//DCC 的数量,且是用来编号的
int dfn[N],low[N],cnt,num;
int n,m,root;
int stk[N],top;
int cut[N];
int new_id[N];

inline void add(int x,int y){
    nex[++tot] = head[x];
    ver[tot] = y;
    head[x] = tot;
}
//缩点就是把原图中的连通块缩成点，图变成一个新的树
int hc[N],nc[M],vc[M],tc;

inline void add_c(int x,int y){
    nc[++tc] = hc[x];
    vc[tc] = y;
    hc[x] = tc;
}

void tarjan(int x){
    dfn[x] = low[x] = ++num;
    stk[++top] = x;
    if(x == root && head[x] == 0){
        dcc[++cnt].push_back(x);//新的连通块
        return ;
    }
    int flag = 0;
    for(int i = head[x];i;i = nex[i]){
        int y = ver[i];
        if(!dfn[y]){
            tarjan(y);
            low[x] = min(low[x],low[y]);
            if(low[y] >= dfn[x]){
                flag++;
                if(x != root || flag > 1)
                    cut[x] = true;
                cnt++;//第cnt个连通块
                int z;
                do{
                    z = stk[top--];
                    dcc[cnt].push_back(z);
                }while(z != y);//这个是在里边
                dcc[cnt].push_back(x);//这里及上面的作用是割点并把分开的连通块存在dcc里
            }
        }
        else low[x] = min(low[x],dfn[y]);
        //割点不用判断父节点
    }
}

int main(){
    cin>>n>>m;
    over(i,1,m){
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);add(y,x);
    }
    over(i,1,n)
    if(!dfn[i])
        root = i,tarjan(i);
    //给每一个割点一个新的编号（编号从cnt+1开始）
    num = cnt;
    over(i,1,n)
    if(cut[i])//是割点就给一个编号//割点就是单独的一个树上的点
        new_id[i] = ++num;
    //建新图，从每一个v-DCC到它包含的所有割点连边
    tc = 1;//初始化
    over(i,1,cnt){
        over(j,0,dcc[i].size()-1){
            int x = dcc[i][j];
            if(cut[x]){//是割点就是单独的一个树上的点
                add_c(i,new_id[x]);
                add_c(new_id[x],i);
            }
            else c[x] = i;//都等于i
            //除了割点以外，其他点仅属于1个v-DCC，一个连通块是一个v-DCC就是树上的一个点
        }
    }
    printf("缩点之后的森林,点数%d,边数%d\n",num,tc / 2);
    printf("编号 1~%d 的为原图的v-DCC,编号 > %d 的为原图割点\n",cnt,cnt);
    for(int i = 2;i < tc;i += 2)
        printf("%d %d\n",vc[i ^ 1],vc[i]);
    return 0;
}

3.解题报告：POJ - 3694 - Network(Tarjan割边缩点 + LCA + 并查集优化)

给定一张N个点M条边的无向连通图，然后执行Q次操作，每次向图中添加一条边，并且询问当前无向图中“桥”的数量。$N\le 10^5,M\le 2\ast 10^5,Q\le 1000$。

先自己思考一会再看下面的题解

解题报告：POJ - 3694 - Network(Tarjan割边缩点 + LCA + 并查集优化)

五、欧拉路问题

欧拉回路就是给一个图，存在一条回路把所边经过且每条边只经过一次。

对于无向图：

存在欧拉回路的条件：每个点的度都为偶数；
　　
存在欧拉路的条件：有且只有两个点的度为一，且这两个点分别为起点和终点；

对于有向图：

存在欧拉回路的条件：每个点出度等于入度；

存在欧拉路的条件：存在一个点出度比入度多一作为起点，存在一点入度比出度多一作为终点，其余点出度等于入度；

求欧拉回路的方法——基本（套圆）法
　　dfs搜索，不能再往下走便回溯，回溯时记录路径，回溯时不清除对边的标记，最后求出来的路径就是欧拉回路。

（1）走$<1,2>,<2,3>,<3,4>,<4,5>,<5,1>$,然后无路可走，就回溯记录下回溯路径$<1,5>,<5,4>$,4点有其它路壳走。
（2）$<4,8>,<8,3>,<3,6>,<6,7>,<7,2>，<2,4>$,无路可走，然后回溯$<1,5>,<5,4>,<4,2>,<2,7>,<7,6>,<6,3>,<3,8>,<8,4>,<4,3>,<3,2>,<2,1>$。
记录下的路径$<1,5>,<5,4>,<4,2>,<2,7>,<7,6>,<6,3>,<3,8>,<8,4>,<4,3>,<3,2>,<2,1>$便是一条欧拉回路。

上述的时间复杂度为$O(NM)$。因为一个点会被重复遍历多次。
假设我们采用邻接表存储无向图，我们可以在访问一条边$(x,y)$后，及时地修改表头$head[x]$，令它指向下一条边，这样我们每次只需取出$head[x]$,就自然跳过了所有已经访问过的边。（vis数组突然就没什么用了）

另外，因为欧拉回路的DFS的递归层数是$O(M)$级别的，很容易造成系统栈的溢出，我们可以用另一个栈，模拟机器的递归过程，把代码转化为非递归实现，优化后的程序时间复杂度为$O(N+M)$

---

——《算法竞赛进阶指南》

4.解题报告：luogu P6066 [USACO]Watchcow （欧拉回路详解）【模板】

回到本题，由于题目要求每条边要正反走两边，那么我们直接把原求欧拉回路模板的vis数组的双向标记改为单向标记即可。因为按照一般的存储方式，无向边在邻接表中是被拆成了两条有向边来存储，若无标记，根据欧拉回路中的更新方式来看，正好会经过两次。

#include
#include
#include
#include
#include
#include
//#define ls (p<<1)
//#define rs (p<<1|1)
#define over(i,s,t) for(register int i = s;i <= t;++i)
#define lver(i,t,s) for(register int i = t;i >= s;--i)
//#define int __int128
//#define lowbit(p) p&(-p)
using namespace std;

typedef long long ll;
typedef pair<int,int> PII;
const ll INF = 1e18;
const int N = 5e4+7;
const int M = 5e5+7;

int head[N],nex[M],ver[M],tot = 1;
bool vis[M];
int stk[M],ans[M];//模拟系统栈，答案栈
int n,m,s,t,cnt,top;
queue<int>q;

void add(int x,int y){
    ver[++tot] = y;nex[tot] = head[x];head[x] = tot;
}

void euler(){//模拟dfs
    stk[++top] = 1;//起点
    while(top > 0){
        int x = stk[top],i = head[x];
        while(i && vis[i])i = nex[i];//找到一条尚未访问过的路
        // 与x相连的所有边均已访问，模拟回溯过程，并记录
        if(i){
            stk[++top] = ver[i];
            vis[i] =  true;//题目要求要回来的嘛，需要标记一次
            //vis[i] = ver[i ^ 1] = true;//正常的欧拉回路模板
            head[x] = nex[i];
        }
        else {// 与x相连的所有边均已访问，模拟回溯过程，并记录
            top--;
            ans[++cnt] = x;
        }

    }
}

int main(){
    scanf("%d%d",&n,&m);
    tot = 1;
    over(i,1,m){
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);add(y,x);
    }
    euler();
    over(i,1,cnt)
    printf("%d\n",ans[i]);
}