前言
今天\(T1\)快速幂(可惜我假期摸鱼……)\(T2\)是字典树(正解其实应该是AC自动机,但是没人会……)\(T3\)竟然整了一个哈希dp……当场自闭。\(T4\)多种方法,最短路,暴力dp,线段树均可。总的来说就是自闭的一天……(说实话,今天老师选的题真的是开玩笑一样)
NO.1 李时珍的皮肤衣
题目描述
\(LSZ\)很皮!\(LSZ\)的皮肤衣更皮!
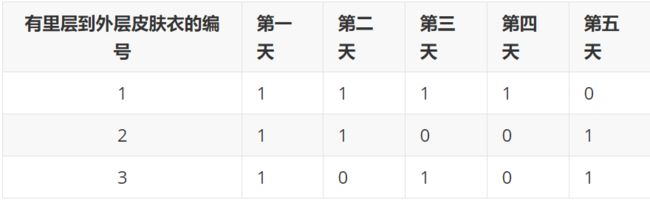
\(LSZ\)有很多件神奇的皮肤衣,而且\(LSZ\)总是喜欢一次穿上多件皮肤衣(一件套一件,而且一直穿好多天),这些皮肤衣有透明或不透明两种状态,当不透明的皮肤衣吸收了一天的阳光直射后,就会变成透明的皮肤衣,透明的皮肤衣能使阳光照射到里层皮肤衣,而透明的皮肤衣再吸收阳光,会在第二天会变成不透明的皮肤衣,不透明的皮肤衣会阻止阳光照射到里层皮肤衣。
\(LSZ\)从某天起(该天算作第\(1\)天)穿上\(N\)件皮肤衣(刚开始所有皮肤衣都是不透明的),问你最少要经过多少天,\(LSZ\)身上的皮肤衣都经历过透明变化?
例如今天(公元\(2018\)年\(6\)月\(17\)日)\(LSZ\)穿了\(3\)件皮肤衣服,会在公元\(2018\)年\(6\)月\(21\)日\(3\)件皮肤衣都会经历过透明变化。
输入格式
一行,只有一个整数\(N\)。
输出格式
最少的天数(对\(N\)取余数)
样例
样例输入1
3
样例输出1
2
样例1解释
使用\(0\)代表皮肤衣透明状态。
使用\(1\)代表皮肤衣不透明的状态。
\(5\)对\(3\)取余数为\(2\)。
样例输入2
5
样例输出2
2
数据范围与提示
\(20\%\)的数据:\(N \le 15\)
\(60\%\)的数据:\(N \le 10^7\)
\(100\%\)的数据:\(N \le 10^{10}\)
分析
看到这个题目一开始是没有思路的,但是可以手模一到两个小数据,然后就会发现,其实这个答案是有规律的。假设\(i\)件,\(g[i]\)为答案,那么手模几个可以发现这个题的规律跟汉诺塔差不多,即\(g[i] = 2\times g[i-1]+1\),相信能做这种题的数列都学过,推个通项公式嘤该没问题(好懒……),最后可以推出来答案应该是\(2^n-1\)。
但是看到数据范围,\(N \le 10^{10}\),开玩笑??所以我们需要快速幂并取模。其实就是个板子,推出来公式就很好写了。
代码
#include
#define ll unsigned long long
ll n;
ll pow(ll a,ll b){//注意如果using namespace std了,并且用的万能库,函数名千万别用pow,有冲突但不报错,我就是这么挂的……
ll ans = 1;//这块就是快速幂板子
ll base = a%n;
while(b){
if((b & 1) !=0){
ans = (ans*base)%n;
}
base = (base*base)%n;
b>>=1;
}
return ans;
}
int main(){//求值,注意过程取模
std::cin>>n;
ll ans = pow(2,n-1);
ll jl = (ans+1)%n;
std::cout< NO.2 马大嘴的废话
题目描述
\(MZH\)爱说废话,喜爱“水群”,经常被“提走”,管理员对\(MZH\)在群里说话进行了限制:
1、只能说小写英文字母。
2、长度不超过\(20\)。
即使这样,也不能阻止\(MZH\)“水群”,他在限制的条件下也说了成千上万条废话信息,现在已知\(MZH\)说过的\(N\)条废话信息,接下来\(MZH\)要说\(M\)条废话信息,请你回答:对于他说的每条废话信息在已知\(N\)条废话信息中出现的次数和(如果一条中出现多次,只算一次)。
比如:\(MZH\)说过了\(3\)条信息
1.adbdb
2.bcde
3.cdbf
4.db
现在说的信息为db,那么信息db在信息1和信息3和信息4出现过,所以答案为3.
输入格式
第一行,一个整数N。
接下来\(N\)行,每行一个字符串(只能由小写字母组成),代表\(MZH\)说过的\(N\)条废话信息。
再接下来一行,一个整数\(M\)。
接下来\(M\)行,每行一个字符串(只能由小写字母组成),代表当前\(MZH\)要说的一条废话信息。
输出格式
共\(M\)行,每行输出该废话信息出现的次数和。
样例
样例输入
20
ad
ae
af
ag
ah
ai
aj
ak
al
ads
add
ade
adf
adg
adh
adi
adj
adk
adl
aes
5
b
a
d
ad
s
样例输出
0
20
11
11
2
数据范围与提示
\(20\%\)的数据:\(n\le 100 , m\le 50\)
\(60\%\)的数据:\(n\le 10^4, m\le 500\)
\(100\%\)的数据:\(n\le 10^4, m\le 10^5\)
分析
题意就是从上边给出的字符串中找出子串含有下边字符串的数量。暴力枚举扫描能过一半的点,后边的就\(TLE\)了。那么正解是什么呢,我们考虑字典树(\(Tire\)树),其实正解应该是AC自动机,但是我没学机房里还有巨佬用的双哈希取模,(开了c++11使用unordered_map达到\(O(1)\)的查询才过,不然会t。)对于我只是搞了搞字典树。其中需要注意的是,因为查询的是子串,所以我们需要把以最后一个字母为后缀的所有子串都存入,这样才能达到全部能搜索到,而且同一字符串内到达一个节点时\(cnt\)不能加。然后就可以进行字典树建树查询了。
代码
#include
using namespace std;
const int maxn = 26;
struct tree{//指针建立结构体。
struct tree *son[26];//儿子指针
int cnt;//记录有多少情况到他
int flag;//记录是第几个字符串,也就是id
}*root;
void insert(char *p,int id){//建树,字符取指针
int i,k,j;
tree *cur=root,*next;//初始化cur为根
int len=strlen(p);
for(i=0;ison[k]!=NULL)//儿子不为空,就让指针指向儿子
cur=cur->son[p[i]-'a'];
else {
next=new(tree);//儿子为空就建一个新指针
for(j=0;j<26;j++)//初始化
next->son[j]=NULL;
next->cnt=0;
next->flag=-1;
cur->son[p[i]-'a']=next;//让空的儿子为下一个
cur=next;//指针指向儿子
}
if(cur->flag!=id)//不是同一个字符串就cnt++,更新id
{
cur->cnt++;
cur->flag=id;
}
}
}
int Find(char *p){//查询
int i;
tree *cur=root;
int len = strlen(p);
for(i=0;ison[k]==NULL){//子节点为空那么肯定没有该子串
break;
}
else{
cur=cur->son[k];//指针指向儿子
}
}
if(icnt;//返回数目
}
int main(){
int n,m;
int i,j;
char s[25];
root = new(tree);
for(int i=0;i<26;i++){
root->son[i]=NULL;
}
root->cnt=0;
root->flag=-1;
scanf("%d",&n);
for(i=1;i<=n;i++){//建树
scanf("%s",s);
for(j=0;s[j];j++){
insert(s+j,i);
}
}
cin>>m;
for(int i=1;i<=m;++i){
cin>>s;
int ans = Find(s);
cout< 暴力代码
#include
using namespace std;
int ans;
char s1[10010][22],s2[22];
int n, m;
int len1[10010],len2;
bool judge(char s1[],char s2[]){
int j,k;
int len = strlen(s2);
int len2 = strlen(s1);
for(int i=0;i>n;
for(int i=1;i<=n;++i){
cin>>s1[i];
len1[i] = strlen(s1[i]);
}
cin>>m;
for(int i=1;i<=m;++i){
cin>>s2;
ans = 0;
int len2=strlen(s2);
for(int j=1;j<=n;++j){
if(len2 > len1[j])continue;
if(judge(s2,s1[j]) == true){
//cout< NO.3 SSY的队列
这个题没有题解,主要是正解还没学……
NO.4 清理牛棚
原型可以自行上百度qaq
题目描述
约翰的奶牛们从小娇生惯养。她们无法容忍牛棚里的任何脏东西。约翰发现,如果要使这群有洁癖的奶牛满意,它不得不雇佣她们中的一些来清扫牛棚。
约翰的奶牛中有\(N(1\le N\le 10000)\)头愿意通过清扫牛棚来挣一些零花钱。由于在某个时段中奶牛们会在牛棚里随时随地地乱扔垃圾,自然地,她们要求在这段时间里,无论什么时候至少要有一头奶牛正在打扫。需要打扫的时段从某一天的第M秒开始,到第\(E\)秒结束\((0\le M\le E\le 86399)\).注意这里的秒是指时间段而不是时间点。也就是说,每天需要打扫的总时间是\(E-M+1\)秒。
约翰已经从每头牛哪里得到了她们愿意接受的工作计划:对于每一头牛,她每天都愿意在第\(T1..T2\)秒的时间段内工作\((M\le T1\le T2\le E)\),所要求的报酬是\(S\)美元\((0\le S\le 500000)\)。与需打扫时段的描述一样,如果一头奶牛愿意工作的时段是每天的第\(10..20\)秒,那她总共工作的时间是\(11\)秒,而不是\(10\)秒。约翰一旦决定雇佣某一头奶牛,就必须付给她全额的工资,而不能只让她工作一段时间,然后再按这段时间在她愿意工作的总时间中所占的百分比来决定她的工资。
现在请你帮约翰决定该雇佣那些奶牛以保持牛棚的清洁,当然,在能让奶牛们满意的前提下,约翰希望使总花费尽量小。
输入格式
第\(1\)行:\(3\)个正整数\(N,M,E\),用空格隔开。
第\(2\)到\(N+1\)行:第\(i+1\)行给出了编号为\(i\)的奶牛的工作计划,即\(3\)个用空格隔开的正整数\(T1,T2,S.\)
输出格式
输出一个整数,表示约翰需要为牛棚清理工作支付的最少费用。如果清理工作不可能完成,那么输出\(-1\).
样例
样例输入
3 0 4
0 2 3
3 4 2
0 0 1
样例输出
5
数据范围与提示
约翰有\(3\)头牛。牛棚在第\(0\)秒到第\(4\)秒之间需要打扫。第\(1\)头牛想要在\(0,1,2\)秒内工作,为此她要求的报酬是\(3\)美元,其余的依此类推。
分析
此题有许许多多种,在这里暂时分析一种,因为后边我没有理解,但是我会把代码放上,只能自行理解了……
最短路
这个算法比较巧妙,具体思路主要在建边上,我们把每头奶牛工作时间之间建边,然后边权为报酬,然后在每个时间点之间建边,边权为0,这样就把开始的时间和结束的时间连起来了。当一个点能到达的时候,这个点和起点之间的点一定是全部都被覆盖了的。具体的一种覆盖情况见图解
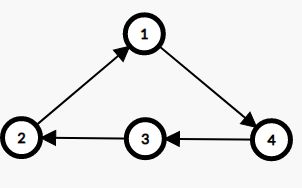
上边是有边权的,下边反着的边没有边权
这样就相当于一种覆盖。只要从题目给的起点到终点全部被覆盖,那么跑一遍最短路就行了。如果到达不了,也就是距离为初始化的最大值,那么输出\(-1\)。值得注意的是,这个建边需要的是时间段的建边,所以建边的时候要把终点加一而达到建的时间段的边。又因为正着是有边权的,逆着的是没有的,所以就可以达到让一头牛可以工作到一半,从另一个时间开始让另一头牛工作的目的。(感性理解一下)
代码
#include
using namespace std;
const int maxn = 3e5+10;
#define ll long long
struct Node{
int v,next;
ll val;
}e[maxn];
int tot;
int head[maxn];
int n,m,E;
void Add(int x,int y,int val){//建边
e[++tot].v = y;
e[tot].next = head[x];
e[tot].val = val;
head[x] = tot;
}
ll dis[maxn];
int vis[maxn];
priority_queue >q;
void Dij(int m){//迪杰斯特拉求最短路,spfa不稳定
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[m] = 0;
q.push(make_pair(0,m));
while(!q.empty()){
int x = q.top().second;
q.pop();
if(vis[x])continue;
vis[x] = 1;
for(int i=head[x];i;i=e[i].next){
int v = e[i].v;
int z = e[i].val;
if(dis[v] > dis[x]+z){
dis[v] = dis[x]+z;
q.push(make_pair(-dis[v],v));
}
}
}
}
int main(){
scanf("%d%d%d",&n,&m,&E);
for(int i=m;iE)y=E;
Add(x,y+1,val);//每头牛时间段之间建边
}
Dij(m);
if(dis[E+1] == 0x3f3f3f3f3f3f3f3f){
printf("-1\n");
}
else {
printf("%lld",dis[E+1]);//到终点的最短路
}
return 0;
}
暴力dp代码
#include
using namespace std;
const int maxn = 1e4+10;
const int maxm = 9e4+10;
struct Node{
int l,r,w;
}a[maxn];
int f[maxm];
int n,m,E;
bool cmp(Node a,Node b){
if(a.r == b.r)return a.l>n>>m>>E;
for(int i=1;i<=n;++i){
cin>>a[i].l>>a[i].r>>a[i].w;
}
sort(a+1,a+n+1,cmp);
memset(f,0x3f,sizeof(f));
for(int i=1;i<=n;++i){
if(a[i].l<=m)f[i] = a[i].w;
}
for(int i=2;i<=n;++i){
for(int j=i-1;j>0;--j){
if(a[i].l <= a[j].r+1){
f[i] = min(f[i],f[j]+a[i].w);
}
else break;
}
if(a[i].r>=E)ans = min(ans,f[i]);
}
if(ans == 0x3f3f3f3f){
cout<<"-1"< 单调队列优化dp
#include
#include
#include
using namespace std;
const int lqs=1e4+10,INF=0x7f7f7f7f;
struct Node{
int st,et,fee;
bool operator <(const Node &A)const{
if(et==A.et)return st>1;
if(p[que[mid]].et=f[i])tt--;
if(p[que[tt]].et