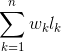java 实现哈夫曼树
一、 什么是哈夫曼树
要理解什么是哈夫曼树，首先要理解几个概念
路径：从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。
路径长度：路径上的分支数目。
树的路径长度：从树根到每一个结点的路径长度之和。（完全二叉树就是树的路径长度最短的二叉树）
考虑带权的结点
结点的带权路径长度：从该结点到树根之间的路径长度和结点上权的乘积。
树的带权路径长度：树的所有结点的带权路径之和（WPL）
WPL = 
假设有 n 个权值为{ 
, 
, ...
} ，是构建一颗有 n 个叶子结点的二叉树，每个叶子结点带权为 
，则其中带权路径长度 WPL 最小的二叉树称为 最优二叉树 或 哈夫曼树。
假设有四个结点a、b、c、d，权值分别为 7、5、2、4
他们的带权路径分别为：
（1）WPL=7x2+5x2+2x2+4x2=36
（2）WPL=7x3+5x3+2x1+4x2=46
（3）WPL=7x1+5x2+2x3+4x3=35
其中（3）树的 WPL 值最小。可以验证，他恰为哈夫曼树，即其带权路径长度在所有带权为 7，5，2，4 的 4 个叶子节点的二叉树中最小。
二、哈夫曼树的应用
哈夫曼树应用于哈夫曼编码的生成，进而实现压缩。
例如有 A B A C C D A ，它只有四个字符，只需要两个字符的串便可以分辨，假设 A , B, C, D 的编码分别为 00，01，10，11，则上述 7 个字符可变为 00010010101100，总长为 14 ，之后可以按两位一分来进行译码。
当然，我们总是希望能用尽可能短的编码来将信息进行压缩。如果我们将 A，B，C，D 的编码设为 0，00，1，01，则上述七个字符可转化为 000011010 ，但是这样的编码无法翻译，就算是前面四个编码 0000 ，就可以翻译为 AAAA 或 ABA 或 BB 等。因此，若要设计长短不一的编码，则必须保证任一个字符的编码都不是另一个字符的编码的前缀。
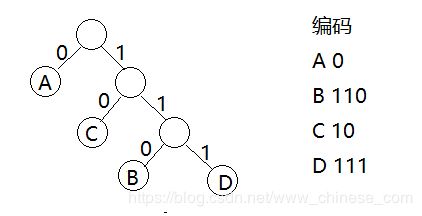
可以利用二叉树来设计二进制的前缀编码，且约定 左分支表示字符 ‘0’，右分支表示字符 ‘1’ ，当字符都作为这个二叉树的叶子结点时，可以实现 “任一个字符的编码都不是另一个字符的编码的前缀”，
当这颗二叉树为哈夫曼树时，所翻译得到的编码数量最少。
如图，A，B，C，D这四个字符
因此，上述字符可翻译为 0110010101110 总长为 13 。当字符种类越多，各个字符所构建的结点的权值相差越大时，压缩的效果越明显。
三、哈夫曼树的实现。
哈夫曼最早给出了一个带有一般规律的算法，俗称哈夫曼算法：
（1）根据给定的 n 个权值 { , , ... } 构成 n 棵二叉树的集合 F = { 
,
, ... ,
} ，其中每棵二叉树 
只有一个权值为 的根结点，其左、右子树均为空。
（2）在 F 中选取两棵根结点的权值最小的树作为左、右子树构造一棵新的二叉树，且置新的二叉树的根结点的权值为左、右子树上根结点的权值之和。
（3）在 F 中删除这两棵树，同时将新得到的二叉树加入到 F 中。
（4）重复（2）和（3），直至 F 中只含有一棵树为止。这棵树便是哈夫曼树。
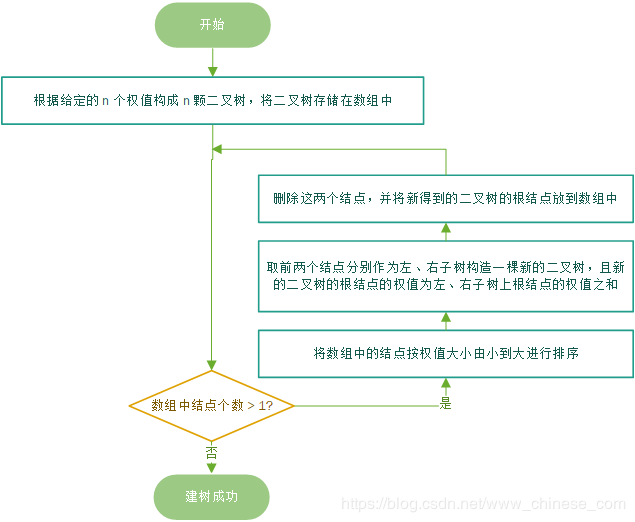
在具体实现时，根据给定的 n 个权值构成 n 颗二叉树，将二叉树存储在数组中，在最开始的时候，数组中每一个根结点的左、右子树均为空，
当数组中的结点数大于 1 时，将数组中的结点按权值大小由小到大进行排序，取前两个结点（即权值最小的两个结点）分别作为左、右子树构造一棵新的二叉树，且新的二叉树的根结点的权值为左、右子树上根结点的权值之和（即选取出来的两个结点的权值之和），在数组中删除这两个结点，并将新得到的二叉树的根结点加入到数组中。
下面是步骤及代码
（1）构建结点类
public class Node {
int pow;// 结点中字符的权值
String c;// 结点中的字符
/**
* 要存储在树结点中的数据
*
* @param pow 结点中字符的权值
* @param c 结点中的字符
*/
public Node(int pow, String c) {
this.pow = pow;
this.c = c;
}
}
（2）构建树结点类
public class TreeNode {
Node node;//要存储在树结点中的数据
TreeNode left;//左子树
TreeNode right;//右子树
public TreeNode() {
}
public TreeNode(Node node) {
this.node = node;
}
}（3）根据给定的 n 个权值构成 n 颗二叉树，将二叉树存储在数组中
ArrayList array = new ArrayList();
// 将存在的字符的树结点存在array中，用于排序
public void setArrayList() {
// n个数据 w[i]为第 i 个数据的权值 ,s[i]为第 i 个数据的内容（字符）
for(int i = 0;i < n;i++) { // n个数据
TreeNode tNode = new TreeNode(new Node(w[i],s[i])); /
array.add(tNode);
}
} （4）将数组中的结点按权值大小由小到大进行排序（插入排序）
public void sort() {
// 认为i前面的数据都是有序的，从第二个数开始遍历，
// 记住开始的位置，记住开始的结点，当遇到第一个比它小的数时，
// 检验此时的位置j是否和开始的位置相同，若相同，则不用变化
// 若不相同，删除上一次的位置，将这个结点插入到现在这个位置
for (int i = 1; i < array.size(); i++) {
int min = i;
int j;
TreeNode tNode = array.get(i);
for (j = i; j > 0; j--) {
TreeNode lastNode = array.get(j - 1);
if (tNode.node.pow > lastNode.node.pow)
break;// 找到第一个比他小的数据时。退出循环
}
min = j;
if (min != i) {// 如果，min值发生变化，即前面有比pow大的数
array.remove(tNode);
array.add(min, tNode);
}
}
}（5）取前两个结点分别作为左、右子树构造一棵新的二叉树，且新的二叉树的根结点的权值为左、右子树上根结点的权值之和
public TreeNode product(TreeNode left, TreeNode right) {
TreeNode tNode = new TreeNode(new Node(left.node.pow + right.node.pow, left.node.c + right.node.c));// 生成的结点
tNode.left = left;
tNode.right = right;
return tNode;
}（6）在数组中删除这两个结点，并将新得到的二叉树的根结点放到数组中（当数组中的结点个数大于1时，不断反复这个动作，并在执行完这个操作后，再次排序）
以下代码将这个哈夫曼树的过程连起来（作参考，直接运用编译不会通过）
TreeNode root;// 树的头结点
public Huffman() {
setArrayList();// 将其存入链表中
sort();// 将其进行排序
TreeNode tNode = null;
while (array.size() > 1) { // 当链表中的结点数大于1个的时候，将结点不断的加入到哈夫曼树中
tNode = product(array.get(0), array.get(1)); //第 （5） 点
array.remove(0);// 移除原本链表中最小的两个结点
array.remove(0);
array.add(0, tNode);
sort();// 再将新的链表进行排序
}
root = tNode;
}