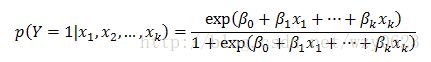MADlib——基于SQL的数据挖掘解决方案（13）——回归之逻辑回归
一、逻辑回归简介
在回归分析中，因变量 y 可能有两种情形：（1）y 是一个定量的变量，这时就用通常的回归函数对 y 进行回归；（2）y 是一个定性的变量，比如y=0或1，这时就不能用通常的回归函数进行回归，而是使用所谓的逻辑回归（Logistic Regression）。逻辑回归方法主要应用在研究某些现象发生的概率p ，比如股票涨跌、公司成败的概率。逻辑回归模型的基本形式为：
其中，
类似于多元线性回归模型中的回归系数。该式表示当自变量为
时，因变量p为1的概率。对该式进行对数变换，可得：
至此，我们会发现，只要对因变量p按照
的形式进行对数变换，就可以将逻辑回归问题转化为线性回归问题，此时就可以按照多元线性回归的方法会得到回归参数。但对于定性实践，p的取值只有0和1（二分类），这就导致
形式失去意义。为此，在实际应用逻辑回归模型的过程中，常常不是直接对p进行回归，而是先定义一种单调连续的概率π，令
有了这样的定义，逻辑回归模型就可变形为：
虽然形式相同，但此时的π为连续函数。然后只需要对原始数据进行合理的映射处理，就可以用线性回归方法得到回归系数。最后再由π和p的映射关系进行反映射而得到p的值。
二、MADlib的逻辑回归相关函数
MADlib中的二分类逻辑回归模型，对双值因变量和一个或多个预测变量之间的关系建模。因变量可以是布尔值，或者是可以用布尔表达式表示的分类变量。在该模型中，训练函数作为预测变量的函数，描述一次训练可能结果的概率。
1. 训练函数
（1） 语法
逻辑回归训练函数形式如下：
logregr_train (source_table,
out_table,
dependent_varname,
independent_varname,
grouping_cols,
max_iter,
optimizer,
tolerance,
verbose ) （2） 参数
参数名称 |
数据类型 |
描述 |
source_table |
VARCHAR |
包含训练数据的源表名。 |
out_table |
VARCHAR |
包含输出模型的表名。主输出表列和概要输出表列如表2、3所示。 |
dependent_varname |
VARCHAR |
训练数据中因变量列的名称（BOOLEAN兼容类型），或者一个布尔表达式。 |
independent_varname |
VARCHAR |
评估使用的自变量的表达式列表，一般显式地由包括一个常数1项的自变量列表提供。 |
grouping_cols（可选） |
VARCHAR |
缺省值为NULL。和SQL中的“GROUP BY”类似，是一个将输入数据集分成离散组的表达式，每个组运行一个回归。此值为NULL时，将不使用分组，并产生一个单一的结果模型。 |
max_iter（可选） |
INTEGER |
缺省值20，指定允许的最大迭代次数。 |
optimizer（可选） |
VARCHAR |
缺省值为‘irls’，指定所使用的优化器的名称： ‘newton’或‘irls’：加权迭代最小二乘。 ‘cg’：共轭梯度法。 ‘igd’：梯度下降法。 |
tolerance（可选） |
FLOAT8 |
缺省值为0.0001，连续的迭代次数的对数似然值之间的差异。零不能作为收敛准则，因此当连续两次的迭代差异小于此值时停止执行。 |
verbose（可选） |
BOOLEAN |
缺省值为FALSE，指定是否提供训练的详细输出结果。 |
表1 logregr_train函数参数说明
列名 |
数据类型 |
描述 |
<...> |
TEXT |
分组列，取决于grouping_col输入，可能是多个列。 |
coef |
FLOAT8[] |
回归系数向量。 |
log_likelihood |
FLOAT8 |
对数似然值 |
std_err |
FLOAT8[] |
系数的标准方差向量。 |
z_stat |
FLOAT8[] |
系数的z-统计量向量。 |
p_values |
FLOAT8[] |
系数的P值向量。 |
odds_ratios |
FLOAT8[] |
让步比 |
condition_no |
FLOAT8 |
X*X矩阵的条件数。高条件数说明结果中的一些数值不稳定，产生的模型不可靠。这通常是由于底层设计矩阵中有相当多的共线性造成的，在这种情况下可能更适合使用其它回归技术。 |
num_iterations |
INTEGER |
实际迭代次数。如果提供了tolerance参数，并且算法在所有迭代完成之前收敛，此列的值将会与max_iter参数的值不同。 |
num_rows_processed |
INTEGER |
实际处理的行数，等于源表中的行数减去跳过的行数。 |
num_missing_rows_skipped |
INTEGER |
训练时跳过的行数。如果自变量名是NULL或者包含NULL值，则该行被跳过。 |
。
表2 logregr_train函数主输出表列说明
训练函数在产生输出表的同时，还会创建一个名为
列名 |
数据类型 |
描述 |
source_table |
TEXT |
源数据表名称。 |
out_table |
TEXT |
输出表名。 |
dependent_varname |
TEXT |
因变量名。 |
independent_varname |
TEXT |
自变量名。 |
optimizer_params |
TEXT |
包含所有优化参数的字符串，形式是‘optimizer=..., max_iter=..., tolerance=...’ |
num_all_groups |
INTEGER |
用逻辑回归模型拟合了多少组数据。 |
num_failed_groups |
INTEGER |
有多少组拟合过程失败。 |
num_rows_processed |
INTEGER |
用于计算的总行数。 |
num_missing_rows_skipped |
INTEGER |
跳过的总行数。 |
表3 logregr_train函数概要输出表列说明
2. 预测函数
（1） 语法
MADlib提供了两个预测函数，预测因变量的布尔值，或预测因变量是“真”的概率值。两个函数语法相同。
预测因变量的布尔值的函数：
logregr_predict(coefficients, ind_var)预测因变量是“真”的概率值的函数：
logregr_predict_prob(coefficients,ind_var)（2） 参数
- coefficients：FLOAT8[]类型，来自logregr_train()的模型系数。
- ind_var：自变量构成的DOUBLE数组，其长度应该与调用logregr_train()函数时，由independent_varname参数所赋值的数组相同。
三、逻辑回归示例
1. 问题提出
企业到金融商业机构贷款，金融商业机构需要对企业进行评估。设评估结果为0或1两种形式，0表示企业两年后破产，将拒绝贷款，而1表示企业两年后具备还款能力，可以贷款。在表4中，已知20家企业（编号1-20）的三项评价指标值和评估结果，试建立模型对其他5家企业（编号21-25）进行评估。
企业编号 |
X1 |
X2 |
X3 |
Y |
1 |
-62.8 |
-89.5 |
1.7 |
0 |
2 |
3.3 |
-3.5 |
1.1 |
0 |
3 |
-120.8 |
-103.2 |
2.5 |
0 |
4 |
-18.1 |
-28.8 |
1.1 |
0 |
5 |
-3.8 |
-50.6 |
0.9 |
0 |
6 |
-61.2 |
-56.2 |
1.7 |
0 |
7 |
-20.3 |
-17.4 |
1.0 |
0 |
8 |
-194.5 |
-25.8 |
0.5 |
0 |
9 |
20.8 |
-4.3 |
1.0 |
0 |
10 |
-106.1 |
-22.9 |
1.5 |
0 |
11 |
43.0 |
16.4 |
1.3 |
1 |
12 |
47.0 |
16.0 |
1.9 |
1 |
13 |
-3.3 |
4.0 |
2.7 |
1 |
14 |
35.0 |
20.8 |
1.9 |
1 |
15 |
46.7 |
12.6 |
0.9 |
1 |
16 |
20.8 |
12.5 |
2.4 |
1 |
17 |
33.0 |
23.6 |
1.5 |
1 |
18 |
26.1 |
10.4 |
2.1 |
1 |
19 |
68.6 |
13.8 |
1.6 |
1 |
20 |
37.3 |
33.4 |
3.5 |
1 |
21 |
-49.2 |
-17.2 |
0.3 |
? |
22 |
-19.2 |
-36.7 |
0.8 |
? |
23 |
40.6 |
5.8 |
1.8 |
? |
24 |
34.6 |
26.4 |
1.8 |
? |
25 |
19.9 |
26.7 |
2.3 |
? |
表4 企业还款能力评价表
对于该问题，很明显可以用逻辑回归模型来求解，已知的三项评价指标为自变量，能否贷款的评价结果是因变量。我们可以调用madlib.logregr_train函数，用已知的20条数据进行训练，然后调用madlib.logregr_predict函数对其他5条数据执行预测，还可以用madlib.logregr_predict_prob函数得到预测值为“真”的概率。
2. 建立测试数据表并装载原始数据
通常训练数据与被预测数据是不同的数据集合，因此这里分别建立两个表。
drop table if exists source_data;
create table source_data
(id integer not null, x1 float8, x2 float8, x3 float8, y int);
copy source_data from stdin with delimiter '|';
1 | -62.8 | -89.5 | 1.7 | 0
2 | 3.3 | -3.5 | 1.1 | 0
3 | -120.8 | -103.2 | 2.5 | 0
4 | -18.1 | -28.8 | 1.1 | 0
5 | -3.8 | -50.6 | 0.9 | 0
6 | -61.2 | -56.2 | 1.7 | 0
7 | -20.3 | -17.4 | 1 | 0
8 | -194.5 | -25.8 | 0.5 | 0
9 | 20.8 | -4.3 | 1 | 0
10 | -106.1 | -22.9 | 1.5 | 0
11 | 43 | 16.4 | 1.3 | 1
12 | 47 | 16 | 1.9 | 1
13 | -3.3 | 4 | 2.7 | 1
14 | 35 | 20.8 | 1.9 | 1
15 | 46.7 | 12.6 | 0.9 | 1
16 | 20.8 | 12.5 | 2.4 | 1
17 | 33 | 23.6 | 1.5 | 1
18 | 26.1 | 10.4 | 2.1 | 1
19 | 68.6 | 13.8 | 1.6 | 1
20 | 37.3 | 33.4 | 3.5 | 1
\.
drop table if exists source_data_predict;
create table source_data_predict
(id integer not null, x1 float8, x2 float8, x3 float8, y int);
copy source_data_predict from stdin with delimiter '|' NULL AS '';
21 | -49.2 | -17.2 | 0.3 |
22 | -19.2 | -36.7 | 0.8 |
23 | 40.6 | 5.8 | 1.8 |
24 | 34.6 | 26.4 | 1.8 |
25 | 19.9 | 26.7 | 2.3 |
\.3. 训练回归模型
drop table if exists loan_logregr, loan_logregr_summary;
select madlib.logregr_train ('source_data',
'loan_logregr',
'y',
'array[1, x1, x2, x3]',
null,
20,
'irls' ); 注意本例中我们从列名动态创建自变量数组。如果自变量的数目很大，以至于超过了PostgreSQL对于每个表中最多列数的限制时（一个表中的列不能超过1600个，这是个硬限制），应该建立自变量数组，并存储于一个单一列中。
4. 查看回归结果
\x off
select round(unnest(coef)::numeric,4) as coefficient,
round(unnest(std_err)::numeric,4) as standard_error,
round(unnest(z_stats)::numeric,4) as z_stat,
round(unnest(p_values)::numeric,4) as pvalue,
round(unnest(odds_ratios)::numeric,4) as odds_ratio
from loan_logregr;
结果：
coefficient | standard_error | z_stat | pvalue | odds_ratio
-------------+----------------+---------+--------+------------
-20.3054 | 1101.1738 | -0.0184 | 0.9853 | 0.0000
0.1347 | 24.8599 | 0.0054 | 0.9957 | 1.1442
1.2877 | 49.3232 | 0.0261 | 0.9792 | 3.6243
10.7682 | 581.7361 | 0.0185 | 0.9852 | 47486.3813
(4 rows)5. 使用Logistic回归预测因变量
\x off
select p.id, madlib.logregr_predict(coef, array[1, x1, x2, x3])
from source_data_predict p, loan_logregr m
order by p.id;结果：
id | logregr_predict
----+-----------------
21 | f
22 | f
23 | t
24 | t
25 | t
(5 rows)预测的结果是21、22两家企业应拒绝贷款，其他三家企业可以贷款。
6. 预测因变量为“真”的概率
\x off
select p.id, madlib.logregr_predict_prob(coef, array[1, x1, x2, x3])
from source_data_predict p, loan_logregr m
order by p.id; 结果：
id | logregr_predict_prob
----+----------------------
21 | 1.22296014464276e-20
22 | 1.88777536644339e-27
23 | 0.999993946936041
24 | 1
25 | 1
(5 rows)21、22为“真”的概率几乎为0，其他三个为“真”的概率为1。
7. 在训练数据上执行预测函数
\x off
select p.id, madlib.logregr_predict(coef, array[1, x1, x2, x3]), p.y
from source_data p, loan_logregr m
order by p.id; 结果：
id | logregr_predict | y
----+-----------------+---
1 | f | 0
2 | f | 0
3 | f | 0
4 | f | 0
5 | f | 0
6 | f | 0
7 | f | 0
8 | f | 0
9 | f | 0
10 | f | 0
11 | t | 1
12 | t | 1
13 | t | 1
14 | t | 1
15 | t | 1
16 | t | 1
17 | t | 1
18 | t | 1
19 | t | 1
20 | t | 1
(20 rows) 可以看到，Logistic模型预测的结果与训练数据完全一致。
实际应用中，以下因素对Logistic回归分析预测模型的可靠性有较大影响：
- 样本量问题：Logistic回归分析中，到底样本量多大才算够，这一直是个令许多人困惑的问题。尽管有人从理论角度提出了Logistic回归分析中的样本含量估计，但从使用角度来看多数并不现实。直到现在，这一问题尚无广为接受的答案。一般认为，如果样本量小于100，Logistic回归的最大似然估计可能有一定的风险，如果大于500则显得比较充足。当然，样本大小还依赖于变量个数、数据结构等条件。每一个自变量至少要10例结局保证估计的可靠性。注意：这里是结局例数，而不是整个样本例数。
- 混杂因素的影响：混杂因素一般可以通过三个方面确定：一是该因素对结局有影响；二是该因素在分析因素中的分布不均衡；三是从专业角度来判断，该因素是分析因素与结局中间的一个环节。也就是说，分析因素引起该因素，通过该因素再引起结局。
- 交互作用的影响：交互作用有时也叫效应修饰，是指在该因素的不同水平（不同取值），分析因素与结局的关联大小有所不同。在某一水平上（如取值为0）可能分析因素对结局的效应大，而在另一个水平上（如取值为1）可能效应小。