Logistic Regression、Linear Discriminant Analysis、Shrinkage Methods（Ridge Regression and Lasso）

引言

本篇文章主要偏向于实际应用的目标，我会把详细的python代码专门写在 jupyter notebook上。这篇文章主要介绍了一些关于应用Logistic Regression，LDA和Shrinkage Methods的一些要点，让你在实际应用中可以更好地发挥各个模型的优势，这篇文章全部来自于对An Introduction to Statistical Learning的总结，如果你有相关的统计学基础，你可以很快读懂文章，并结合到实际的应用，如果你没有相应的基础，希望你参考我的这篇文章：学好机器学习必会的统计学知识。

这是与本篇文章相对应地python代码和一些数据集，请点我

Logistic Regression

Default数据集描述，详细信息在第6页。

logistic regression 是一个线性模型用于做分类的，它直接对Y属于某个类别的概率进行建模。比如对于Default数据集来说，Pr(default = Yes | balance, student, income). 这也就是说，对于任何给定的balance, student, income的值，我都可以求出default = Yes的概率。如果我设定阙值为0.3，那么只要Pr(default = Yes | balance, student, income) > 0.3，我就预测default的结果为Yes.

既然logistic regression是对概率进行建模，因此我们需要一个函数的输出在0到1之间。有很多函数符合这个性质，但是在logistic regression中，我们用logistic function，公式如下：

p(X)=eβ0+β1X1+⋯+βpXp1+eβ0+β1X1+⋯+βpXp

那么我们如如何来估算Logistic Regression的要参数呢？答案是用maximum likelihood. 比如，我们对Pr(default = Yes | X)来进行建模，把估算出的一系列参数插入到模型中，使得所有defaulted人的概率接近1，使得所有没有defaulted人的概率接近0. 我们可以把这样的想法写成一个数学公式表达出来：

l(β0,β1,…,βp)=∏i:yi=1p(xi)∏i′:yi′=0(1−p(xi′))

我们目的是找出一系列参数来最大化上面的likelihood函数。

Linear Discriminant Analysis

Logistic regression用logistic函数直接对Pr(Y = k|X = x)建模。而LDA用一种间接的方法去估算这些概率。LDA对每个response中X的分布进行建模，然后用Bayes理论去反转去估算Pr(Y = k|X = x). 如果每个response中X的分布为正态分布，那么LDA与logistic regression模型是非常相似的。LDA相比于logistic regression模型有以下3个优势：

1. 当类别能well-separated时, logistic regression模型的参数估计是非常不稳定的，而LDA并没有这样的问题。
2. 如果数据集中的样本很少并且每个类别中的X是接近正态分布的，那么LDA也要比logistic regression模型更加稳定。
3. 当我们的response超过2个类别时，LDA是更受欢迎的。

假设我们一共有k个类别，Bayes 理论可以写成如下公式：

Pr(Y=k|X=x)=πkfk(x)∑Kl=1πlfl(x)

• πk: 第k个类别的prior probability
• fk(x): 第k个类别中X的density function
• 以后我们会把Pr(Y = k | X = x)简写成 pk(X) ，称为posterior probability

LDA总体的思路已经被浓缩在上面的一个公式中了。LDA的主要目标就是估算出prior probability和density function，之后我们就可以在给定X的情况下，分别求出属于各个类别的概率。想要估算出density function，我们必须假设它的形式，在LDA中，我们的假设都是正态分布。

只有一个特征的LDA

我们已经假设 fk(x) 是normal的，在one-dimensional的情况下，normal density的形式如下：

fk(x)=12π‾‾‾√σkexp(−12σ2k(x−μk)2)

• μk: 第k个类别的mean
• σ2k: 第k个类别的variance

LDA不仅仅假设X的density function是正态的，而且它还假设 σ21=σ22=⋯=σ2k ，即每个类别中，X分布的方差相等。现在，我把上面的公式插入到Bayes 理论那么公式中，由于所有的方差相同，我简化写成 σ2

pk(x)=πk12π√σexp(−12σ2(x−μk)2)∑Kl=1πl12π√σexp(−12σ2(x−μl)2)

由于我们最终的目标是做分类，我们只要求出在给定X的情况下，属于各个类别的概率，哪个概率最大，最后我们就预测属于哪个类别。因此，我们可以继续简化上面的公式，在简化过程中，算每个类别概率都会用到的项我直接舍弃，过程如下：

ln⎛⎝⎜⎜⎜πkexp(−12σ2(x−μk)2)∑Kl=1πlexp(−12σ2(x−μl)2)⎞⎠⎟⎟⎟lnπk−12σ2(x−μk)2−ln(∑l=1Kπlexp(−12σ2(x−μl)2))lnπk−12σ2(x−μk)2x⋅μkσ2−μ2k2σ2+lnπk−x22σ2

因此，最终公式如下：

δk(x)=x⋅μkσ2−μ2k2σ2+lnπk

最终，哪个 δk(x) 大，我们就预测为哪个类别。上面有三个未知量需要估算， μk 的估算公式如下：

μk^=1nk∑i:yi=kxi

• nk: 第k个类别observations的数量

σ2 的估算公式如下：

σ̂ 2=1n−K∑k=1K∑i:yi=k(xi−μk^)2

• n：total number of training observations

prior probability最好是问一下你应用领域的专家，由于很多原因，训练集并不一定很好地估计出prior probability. 如果你实在没有专家可以咨询，那么就用下面这个简单的公式：

πk^=nkn

总结来说：LDA分类器假设每个类别中的X服从正态分布，并且每个分布都具有一样的方差，之后插入这些估算的参数到Bayes classifier，进而估算每个类别的概率。

多个特征的LDA

先前只有一个特征的LDA，我们假设X服从正态分布。这回具有多个特征的LDA也是相似的道理，只不过是X的分布为多变量Gaussian分布，我们记作

X∼N(μ,∑)

• μ： X的mean（a vector with p component）
• Σ = Cov(X)：p × p covariance matrix of X

multivariate Gaussian density function的公式如下：

f(x)=1(2π)p/2∣∣∑∣∣1/2exp(−12(x−μ)T∑−1(x−μ))

就像上面的单变量LDA一样，通过一些化简，我们可以得出下面的公式：

δk(x)=xT∑−1μk−12μTk∑−1μk+lnπk

Quadratic Discriminant Analysis

QDA的假设要比LDA更松一些，LDA的假设为X分布的方差都一样，而QDA并没有这样的假设。如果你自己动手化简上面的过程，你就会明白当各个类别内X的方差不一样时，就会导致化简结果出现 x2 项。因此，我们才叫它Quadratic Discriminant Analysis.

大致上来说，如果training observations相对较少，LDA的性能要比QDA要好，因为LDA减少了方差。如果training set是非常大的，QDA是更好地选择，因为分类器地方差并不是我们主要考虑地对象。或者当方差相等的假设不成立时，QDA也是一个更合理地选择。

如果QDA模型中假设covariance matrices是diagonal，这就意味着我们假设各个类别中的分布是conditionally independent，因此导致我们的分类器与 Gaussian Naive Bayes是等价的。

几个分类方法之间的比较

logistic regression和LDA之间唯一的不同就是估算参数的方式。logistic regression用 maximum likelihood 估算参数，而LDA假设分布为正态分布从而估算方差和平均值。

LDA假设observations来自于Gaussian distribution，每个类之间有同样的covariance matrix，因此当假设成立时，它的性能要比logistic regression好。但是，如果假设不成立，logistic regression要比LDA表现地更好。

当真正地决策边界是线性的时候，LDA和logistic regression模型性能会很好。当决策边界是稍微非线性的，QDA可能会给出更好地结果。最后，如果决策边界是高度非线性的，non-parametric方法KNN可能会更有优势，前提是我们选择出一个合适的K值。

如果我们想要logistic regression去学习非线性的关系时，我们可以transformations of the predictors，也就是在模型中加入 X2、X4 等高阶项。这样增加flexibility会导致增加variance，但是减少了bias，模型结果的好坏取决于是否减少的bias大于增加的variance.

Shrinkage Methods

shrinking the coefficient estimates 可以明显显著地减小方差。shrinking regression coefficients接近0的2个最著名的技术是ridge regression 和 the lasso

ridge regression

least squares估算线性回归系数时最小化residual sum of squares (RSS)，而Ridge regression是和它相似的，只不过加上正则化项，即L2-penalty，因此，ridge regression最小化：

RSS+λ∑j=1pβ2j

tuning parameter λ 控制两个项之间的平衡，当 λ=0 时， 相当于没有penalty项，ridge regression和least squares一样。然而，当 λ→∞ 时，ridge regression估算的系数都将接近于0.

当我们用least squares去估算系数时，它是scale invariant. 也就是说，把 Xj 乖上一个常数c，least squares估算的系数会缩小为先前的1/c，不管你怎样缩放变量， βj^Xj 将保持不变。但是，ridge regression加上penalty项后，事情就不像先前那样了。

假设你的机器学习应用中，有个长度变量，它的单位是cm，如果你把它的单位变成m，也就是这个变量缩小了100倍，ridge regression产生的系数就和先前不一样了，因为如果你想把估算的系数在扩大100倍，但penalty项并不会允许你这样做，因为这会增加penalty项的大小，导致整体的loss增加。因此，在使用ridge regression之前，一定要standardizing the predictors，让它们在same scale上。

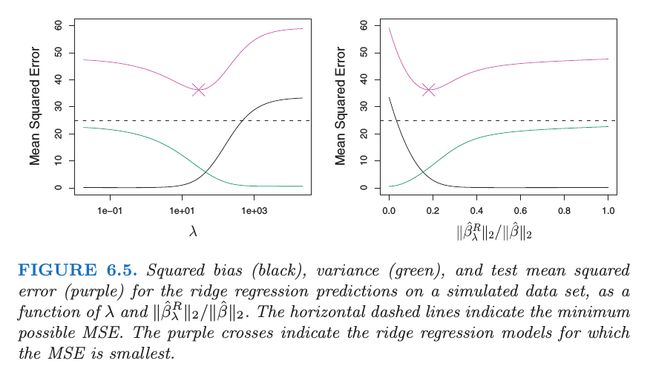
ridge regression相比于least squares的优势在于它植入了bias-variance
trade-off. 随着 λ 增加，ridge regression的flexibility减小，导致减少方差增加偏差。

从上图我们可以看出，随着 λ 逐渐增加，导致显著地减小方差，而只稍微增加偏差。因此，只要我们选择一个合适的 λ ，我们就可以显著地提升模型效果。

The Lasso

ridge regression在最终的模型上会包含所有的predictors，正则项 λ∑β2j 将shrink所有的系数接近0，但是它不会让某个项等于0. 而Lasso可以解决这个问题。 The Lasso 最小化：

RSS+λ∑j=1p∣∣βj∣∣

The Lasso也叫做L1-penalty，它生成sparse models，即只包含了变量的子集。

比较ridge regression和lasso

当小部分的predictors对response有实质的影响，而其余的predictors相关联的系数很小或接近于0，在这种情况下，lasso的性能要比ridge regression要好。当大部分的predictors都与response有关，并且相关联的系数大小基本上相等，在这种情况下，ridge regression的性能要好。然而，在实际应用中，我们不可能事先知道有多少predictors与response相关联，因此，cross-validation是一个好的技术来判断哪个方法更好。